软件
产品
本期专栏是由毕导近期相关视频所联想到的，本UP没玩过麻将，因此从牌堆剩余牌数反推毕导视频中单人拥有一萬的最大牌数的先验概率分布的计算推导如下：
视频链接如下： 如何成为麻将高手，包你一学就会，一打就废！
假设剩余65张牌，一人一局可拥有13张牌，因此一人有0张（即一张都没有）一万的概率为超几何概率分布。
给出如下定义：
matlab中计算组合数的函数是nchoosek(n,k)，其中n>k,即从n个数抽取k个数的组合数。
即
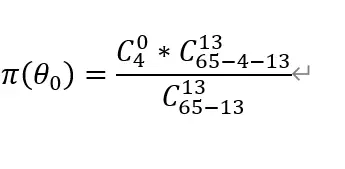
至于pi(theta1,2,3,4) 以此类推。
我们按照毕导给出的前提假设，如下：
由此可得边缘概率分布：
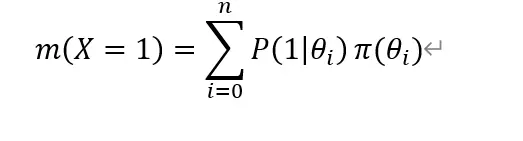
因为就两种情况，m(X=0)=1-m(X=1)
由贝叶斯计算公式，可计算：
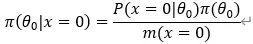
以此类推。
下面给出matlab代码：
主函数为：
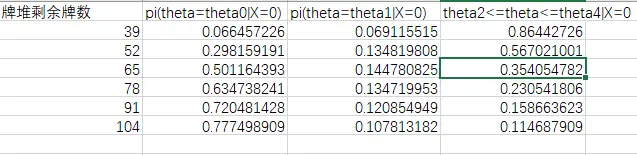
输出的excel表格示例为：
武汉格发信息技术有限公司，格发许可优化管理系统可以帮你评估贵公司软件许可的真实需求，再低成本合规性管理软件许可,帮助贵司提高软件投资回报率，为软件采购、使用提供科学决策依据。支持的软件有: CAD,CAE,PDM,PLM,Catia,Ugnx, AutoCAD, Pro/E, Solidworks 等。
技术文档
推荐好文
155-2731-8020
