MATLAB实验：基本运算与绘图基础

一、        实验要求

1、熟悉MATLAB命令窗口的组成和各菜单的含义；

2、掌握MATLAB基本使用方法，并能熟练操作MATLAB基本命令；

3、掌握函数表达式或模型的输入方法和基本数值计算方法；

4、掌握绘图函数plot的基本使用方法，以及图形各种属性操作。

二、        实验内容

1、已知蝴蝶曲线由以下参数方程给出：

参数方程

                                         

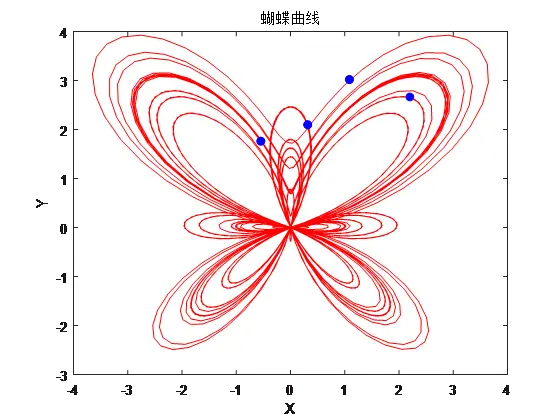
图1-1 蝴蝶曲线

要求如下：

（1）取值范围为[0,100]，步长为1/16（t = 0:1/16:100）；

（2）分别计算和的值（注意表达式中的点乘运算），不要求输出结果，用函数plot(x,y,'r-')绘制蝴蝶曲线；

（3）计算当时的和值，并输出；

（4）使用命令hold on保持当前图像，使用命令plot(x0,y0,'b.','MarkerSize',20)绘制和值到图形中；最终参考图像如图1-1所示。

（5）对工作区中的变量进行截图，并解释各变量的含义和取值；

（6）把上述正确的命令集中录入到命令文件中，命名为“Butterfly_Curve.m”，在命令窗口输入Butterfly_Curve，验证代码功能的正确性和图形的正确性。

2、表1-1是一些关于速度和力的风洞(Wind tunnel)数据。

表1-1 风洞数据

可以用下面的函数描述这些数据：

要求如下：

（1）使用函数plot绘制表1-1风洞数据，用品红色圆形符号表示，圆形符号填充色为青色，使用help plot命令查看函数参数的使用方法；

（2）使用函数plot绘制函数，使用黑色点划线，绘制函数从到之间的部分；

（3）标记坐标轴，标记标题，标记图例，绘制网格。最终参考图形如图1-2所示。

（4）计算表1-1中速度的函数值FT，并与表1-1中F做比较，即计算平均误差（公式为），这里取风洞数据真实测量值F，取相应的函数模型估计值FT，（其中用到sum、abs和length函数）；

（5）把上述正确的命令集中录入到命令文件中，命名为“Wind_tunnel.m”，在命令窗口输入Wind_tunnel，验证代码功能的正确性和图形的正确性。

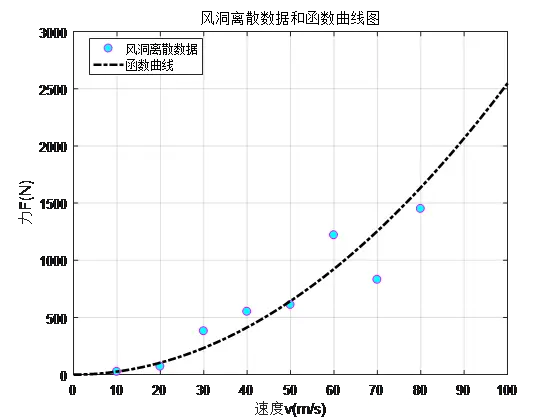
图1-2 风洞数据和函数曲线参考图

3、物体的运动轨迹可以建模为：

其中，是高度（m），是初始角度（弧度），是水平位移（m），是重力加速度（取），是初始速度（m/s），是初始高度。

根据课件案例“电容电量”的求解步骤，完成如下要求：

（1）建立命令文件“Sport_model.m”，按要求输入命令代码，（注意：边输入边验证代码的正确性）；

（2）用MATLAB绘制物体的轨迹，其中，，初始角度从到，步长取。水平距离从变化到，递增步长取；

（3）计算结果应该存放在一个矩阵中，矩阵的第一维度（行）对应于水平距离，而第二维度对应于不同初始角度的高度（从第2行到第6行）；

（4）针对每个初始角度，用该矩阵绘制一幅高度随水平距离变化的图；

（5）使用图例区分不同的情况，用axis命令对图形进行缩放以使最小高度变为，并标记坐标轴和标题。最终参考图形如图1-3所示。

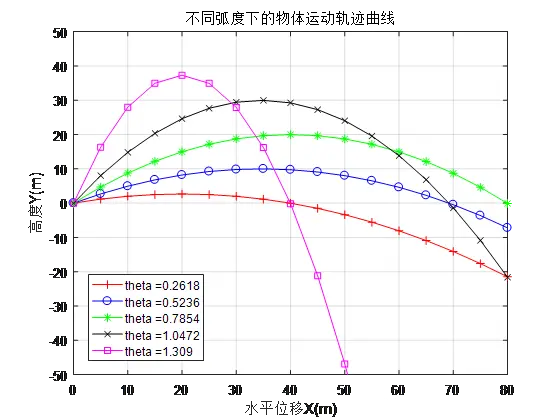
图1-3 不同弧度下的物体运动轨迹图

4、已知分段函数：

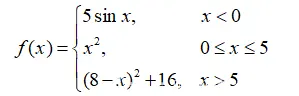
公式：分段函数

要求如下：

（1）用plot函数绘制分段函数，取值范围为[-5, 10)（表示方法可以-5:0.1:10-eps）；

（2）求在点x0 = [0,3,5,8]的函数值，并把此四个点的值绘制在图形中，绘图结果如图1-4所示；

（3）思考如何使用不同颜色绘制不同区间函数的曲线，如图1-5所示。

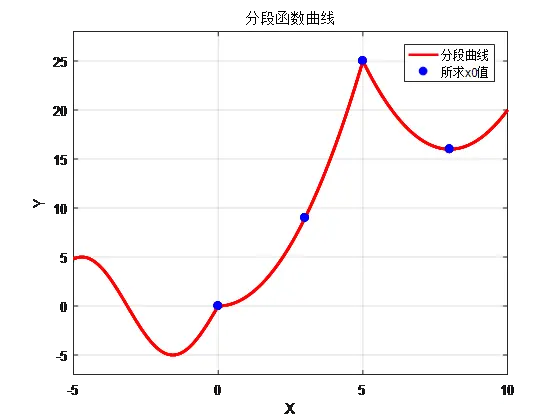
图1-4 分段函数参考图

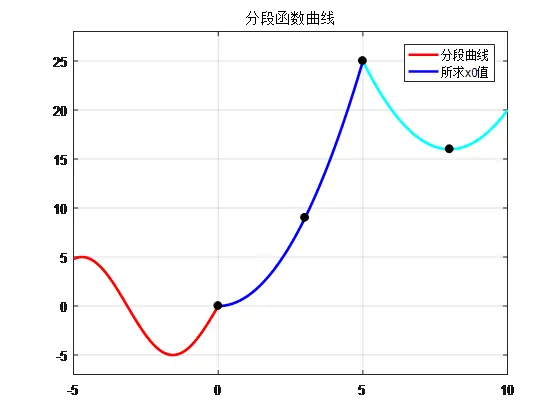
图1-5 不同颜色标记分段函数参考图

5、绘图练习，逐条输入以下语句，观察所绘制图形的变化，并理解熟记绘图属性函数，如set、xlabel、legend、title、text、axis。结果如图1-6所示。（提示：每输入一条语句，观察图形的变化，深刻理解每条语句的含义。特别注意：在输入代码的时候，如果此行代码无误，请把此行代码复制到脚本文件中保存，以便重复利用！！）

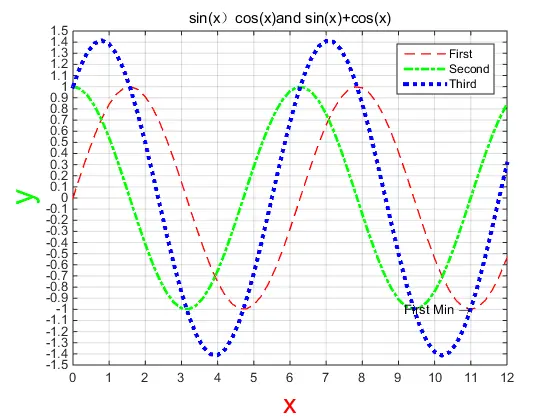
图1-6 绘图结果

%---------------------------------------------代码start-------------------------------------------

%注意以下代码中%后的为注释内容！！

>> x=0:0.2:12; 

>> y1=sin(x); 

>> y2=cos(x); 

>> y3=sin(x)+cos(x);   %计算函数值

>> h=plot(x, y1, x, y2, x, y3);  %绘制基本图形

>> set(h,{'LineWidth'},{1;2;3})   %set(h,{'LineWidth'},{2})==set(h,'LineWidth',2),将所有线宽设置为2

>> set(h,{'Color'},{'r';'g';'b'},{'LineStyle'},{'--'; '-.'; ':'})   %设置颜色和线宽

>> axis([0 12 -1.5 1.5])   %设置坐标轴范围

>> grid on  %添加网格线

>> X=0:1:12;   Y=-1.5:0.1:1.5;

>> set(gca,'xtick',X,'ytick',Y)   %设置网格的显示格式,gca获取当前figure的句柄

>> set(xlabel('x'),'FontSize',20,'Color','r')  %设置X轴坐标值的颜色和大小

>> y=ylabel('y'); 

>> set(y,'FontSize',24,'Color','g')

>> legend(h,'First','Second','Third')      %添加图例

>> title('sin(x）cos(x)and sin(x)+cos(x)')     %添加标题

>> [y,ix]=min(y1);    %找到y1的最小值以及改值的下标，赋给y和ix

>> text(x(ix),y,'First Min \rightarrow','HorizontalAlignment','right')   %插入文本

%-------------------------------------------代码end-------------------------------------------