太阳黑子变化规律预测：Matlab仿真研究

1.软件版本

matlab2013b

2.本算法理论知识

太阳黑子是人们最早发现也是人们最熟悉的一种太阳表面活动。因为太阳内部磁场发生变化，太阳黑子的数量并不是固定的，它会随着时间的变化而上下波动，每隔一定时间会达到一个最高点，这段时间就被称之为一个太阳黑子周期。太阳黑子的活动呈现周期性变化是由施瓦贝首次发现的。沃尔夫 (R.Wolfer)继而推算出11年的周期规律。实际上，太阳黑子的活动不仅呈11年的周期变化，还有海耳在研究太阳黑子磁场分布时发现的22年周期；格莱斯堡等人发现的80年周期以及蒙德极小期等。由于太阳黑子的活动规律极其复杂，时至今日科学家们仍在努力研究其内在的规律和特性。事实上，对太阳黑子活动规律的研究不仅具有理论意义，而且具有直接的应用需求。太阳黑子的活动呈现周期性变化的，沃尔夫(R.Wolfer)根据在过去的288 年(1700年~1987 年)间每年太阳黑子出现的数量和大小的观测数据推算出11 年的周期规律。我们利用Matlab强大的数据处理与仿真功能，对Wolfer数进行功率谱密度分析从而可以得到对太阳黑子活动周期的结论。

使用的线性模型为

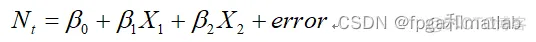
这个部分的MATLAB代码为：

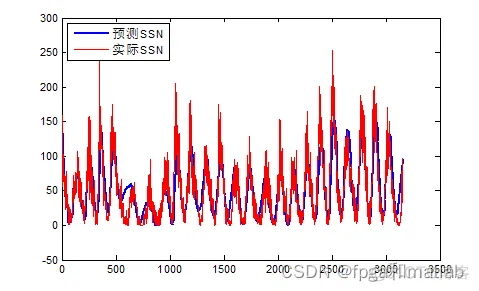
现象模型的预测结构如下：

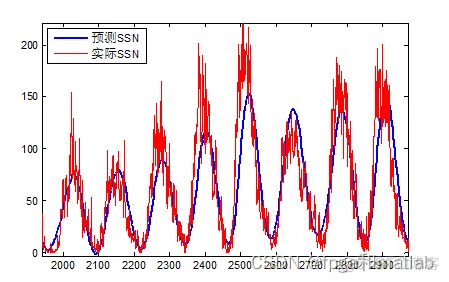
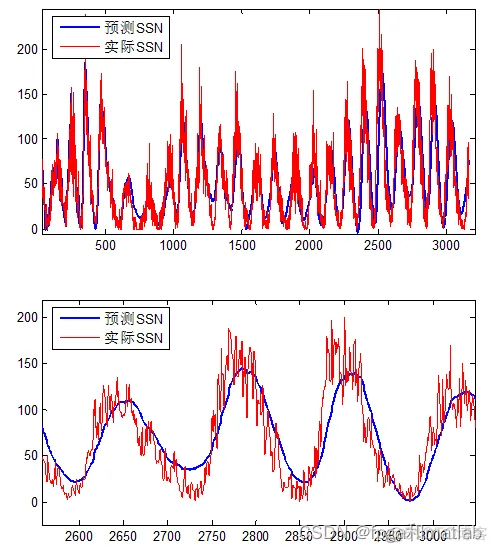
将上面的图放大之后，得到的局部估计效果如下图所示：

然后通过多变量的最小二乘法进行模型预测。引入多个变量作为参数估计，这里，将最小二乘法的估计函数为：

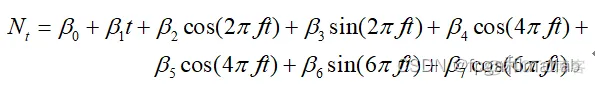
由于从历年的数据可知，虽然总体上数据呈现出周期波形，但是对于每个周期中的波形，其中的局部图中会出现部分高频周期量，所以在估计的时候，这里加上更高频率的分量。使用和上面所讲的最小二乘法进行上述参数的估计。

这个步骤，得到的仿真结果如下图所示：

3.部分源码

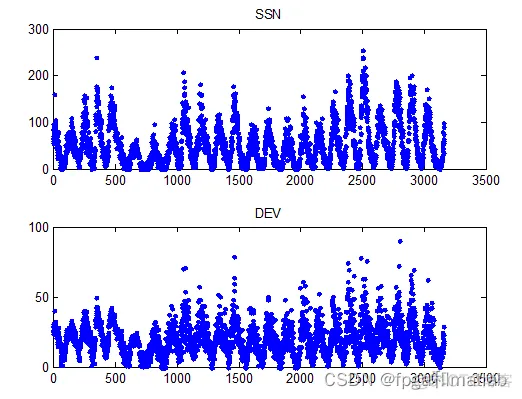
clc;clear;close all;warning off;load Sunspot.txt%YEAR MON  SSN   DEV%画出导入的活动数据YEAR = Sunspot(:,1);
MON  = Sunspot(:,2);SSN  = Sunspot(:,3); %sun spot number DEV  = Sunspot(:,4); %标准偏差表figure;subplot(211);
plot(SSN,'b.');title('SSN');subplot(212);plot(DEV,'b.');title('DEV');
addpath 'funcs\'%step1:Devise and/or employ methods to ?nd the best frequency for the sunspot cycle.
%step1:Devise and/or employ methods to ?nd the best frequency for the sunspot cycle.%step1:
Devise and/or employ methods to ?nd the best frequency for the sunspot cycle.%找到一种较好的方法计算周期K     = 20;
%前22年数据去除Start = 12*K+1;mainPeriod = func_cycle_cal(SSN(Start:end));
mainPeriod%Step2:Predict the time of the next solar maximum and minimum.
%Step2:Predict the time of the next solar maximum and minimum.%Step2:
Predict the time of the next solar maximum and minimum.%构建预测模型，预测后面的最大值和最小值对应的时间%构建预测模型，
预测后面的最大值和最小值对应的时间c0  = [1 1 1 1 1 1 1 1]';%直接给出被辨识参数的初始值,即一个充分小的实向量 p0  = 10^6*eye(8,
8);       %直接给出初始状态P0，即一个充分大的实数单位矩阵 t   = 1/(12):1/(12):length(SSN)/(12);
yc  = cos(2*pi*t/mainPeriod);ys  = sin(2*pi*t/mainPeriod);yc2 = cos(2*pi*t/(2*mainPeriod));
ys2 = sin(2*pi*t/(2*mainPeriod));yc3 = cos(2*pi*t/(3*mainPeriod));ys3 = sin(2*pi*t/(3*mainPeriod));
for k=1:length(SSN); %开始求K     h1     =[1,k,yc(k),ys(k),yc2(k),ys2(k),yc3(k),ys3(k)]';
x      = h1'*p0*h1 + 99;     x1     = inv(x);                  %开始求K(k)     k1     = p0*h1*x1;
%求出K的值     d1     = SSN(k)-h1'*c0;     c1     = c0+k1*d1;                %求被辨识参数c     e1     = c1-c0; 
%求参数当前值与上一次的值的差值     e2     = e1./c0;                  %求参数的相对变化     e(:,k) = e2;
%把当前相对变化的列向量加入误差矩阵的最后一列            c0     = c1;                      
%新获得的参数作为下一次递推的旧参数     c(:,k) = c1;                      %把辨识参数c 列向量加入辨识参数矩阵的最后一列
p1     = p0-k1*k1'*[h1'*p0*h1+1]; %求出 p(k)的值     p0     = p1;                      
%给下次用 end%估计得到的太阳黑子活动曲线for k=1:length(SSN); %开始求K     
Y_predict2(k) = c(1,k) + c(2,k)*k + c(3,k)*yc(k) + c(4,k)*ys(k) + c(5,k)*yc2(k) + c(6,k)*ys2(k) + c(7,k)*yc3(k)
 + c(8,k)*ys3(k); endfigure;plot(Y_predict2,'b','LineWidth',2);
 hold on;plot(SSN,'r');hold off;legend('预测SSN','实际SSN'); 
 Predict_Len = 100;%定义预测时间长度t   = 1/(12):1/(12):(length(SSN)+Predict_Len)/(12);
 yc  = cos(2*pi*t/mainPeriod);ys  = sin(2*pi*t/mainPeriod);yc2 = cos(2*pi*t/(2*mainPeriod));
 ys2 = sin(2*pi*t/(2*mainPeriod));yc3 = cos(2*pi*t/(3*mainPeriod));ys3 = sin(2*pi*t/(3*mainPeriod));
 ind = 0;for k=1:length(SSN)+Predict_Len; %开始求K     if k <= length(SSN)       
 Y_predict3(k) = c(1,k) + c(2,k)*k + c(3,k)*yc(k) + c(4,k)*ys(k) + c(5,k)*yc2(k) + c(6,k)*ys2(k) + 
 c(7,k)*yc3(k) + c(8,k)*ys3(k);     else           
 %Y_predict3(k) = c(1,end) + c(2,end)*k + c(3,end)*yc(k) + c(4,end)*ys(k) + c(5,end)*yc2(k) + c(6,end)
 *ys2(k) + c(7,end)*yc3(k) + c(8,end)*ys3(k);               c0 = mean(c(1,end:end));       
 c1 = mean(c(2,end:end));       c2 = mean(c(3,end:end));       c3 = mean(c(4,end:end));       
 c4 = mean(c(5,end:end));       c5 = mean(c(6,end:end));       c6 = mean(c(7,end:end));       
 c7 = mean(c(8,end:end));       Y_predict3(k) = c0  + c1*k + c2*yc(k) + c3*ys(k) + c4*yc2(k) + c5*ys2(k) + 
 c6*yc3(k) + c7*ys3(k);        ind           = ind + 1;       Ys(ind)       = Y_predict3(k);    
 endendfigure;plot(Y_predict3,'b','LineWidth',2);hold on;plot(SSN,'r');hold off;legend('预测SSN','实际SSN');
 grid on;%根据预测结果得到下次太阳黑子活动高峰和低峰的时间%前一次高峰日期为 XX           = 59;[Vmax1,Imax1] = max(Ys);
 [Vmax2,Imax2] = max(SSN(length(SSN)-XX:length(SSN)));%3100~3160if Vmax1 > Vmax2   II   =  Imax1;   MM   =  
 Vmax1;    time = (length(SSN) + II-3019);%原数据的最后一个月份+预测后的最大值 - 前一个高峰日期else   II   =  Imax2;  
  MM   =  Vmax2;    time = (length(SSN) + (XX-II)-3019);%原数据的最后一个月份+预测后的最大值 - 
  前一个高峰日期endYears=time/12;fprintf('下次高峰期日期为：%d',round(2000 + Years));fprintf('年\n\n');
  fprintf('最大值为：%2.2f\n\n\n\n',MM);%计算下一次低谷值[Vmin,Imin] = min(Ys);fprintf('下次低峰期日期为：%d',
  round(2012 + Imin/12));fprintf('年\n\n');fprintf('最小值为：%2.2f\n\n',Vmin);1.2.3.4.5.6.7.8.9.10.11.12.13.
  14.15.16.17.18.19.20.21.22.23.24.25.26.27.28.29.30.31.32.33.34.35.36.37.38.39.40.41.42.43.44.45.46.47.48.
  49.50.51.52.53.54.55.56.57.58.59.60.61.62.63.64.65.66.67.68.69.70.71.72.73.74.75.76.77.78.79.80.81.82.83.
  84.85.86.87.88.89.90.91.92.93.94.95.96.97.98.99.100.101.102.103.104.105.106.107.108.109.110.111.112.113.
  114.115.116.117.118.119.120.121.122.123.124.125.126.127.128.129.130.131.132.133.134.135.136.137.138.

免责声明：本文系网络转载或改编，未找到原创作者，版权归原作者所有。如涉及版权，请联系删