MATLAB一行代码实现朴素贝叶斯分类算法‌

朴素贝叶斯分类法是聚类分析的一种方法，关于什么是聚类分析，前文提过：

再提一次，聚类分析的目的就是根据个体的多个参数，对群体进行分类。数学上看就是输入一个多维向量，输出一个标签值。

朴素贝叶斯呢，就是聚类分析的一种，其实也是机器学习的一种。选择一组经过标记类型的数据作为训练集，利用朴素贝叶斯方法计算模型参数，再选择一组数据作为测试集，去看刚才用训练集训练好的模型的分类正确率是多少。

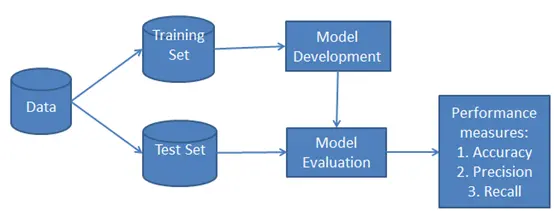
过程

那么，朴素贝叶斯方法如何对数据进行分类呢？

这就得先介绍一下概率统计中的贝叶斯公式：

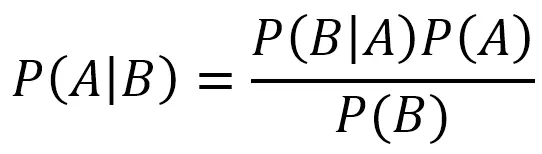
贝叶斯公式

我们都知道条件概率公式

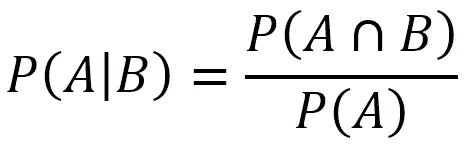
它表示在B发生的情况下A发生的概率。它的公式是AB同时发生的概率除以B发生的概率。

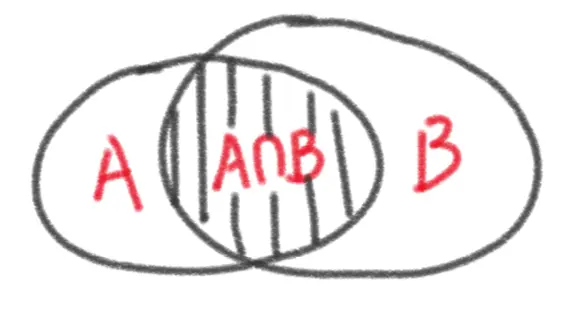
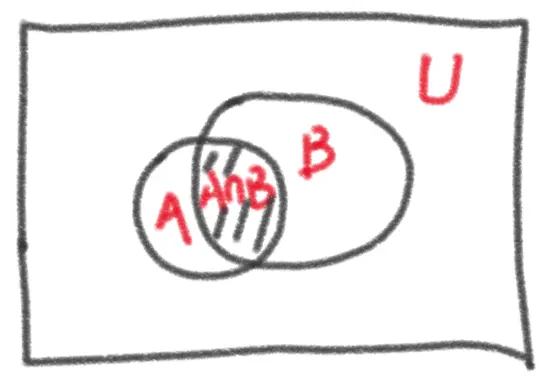
我们从全概空间的角度理解，它限定了全概空间是B，在这一全概空间内发生A的概率就是条件概率。

如图所示：全概空间是U，即U包含了所有可能发生的情况，U对应的“面积”是1，内部的概率大小对应面积大小。AB同时发生的概率就是P(A∩B)，对应阴影面积；如果B已经发生，那么全概空间就“塌缩”成为了B，总面积也缩小为P(B),因此AB同时发生的概率就是阴影面积：P(B)*P(A|B)。

反过来，自然也有在A发生的情况下，B发生的概率。

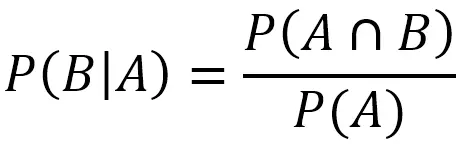
我们把P(A)乘到等式另一边，就得到了下面的式子：

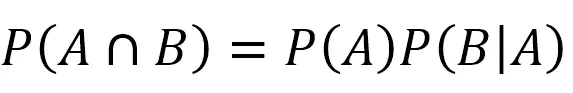
最后一步，我们把P(A∩B)=P(A)P(B|A)代入最开始的式子，我们就得到了贝叶斯公式：

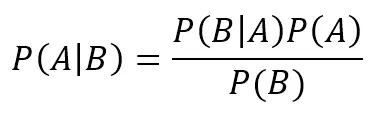
贝叶斯公式

这个公式将A发生的情况下B发生的概率与B发生的情况下A发生的概率联系起来，可以用作预测。

P(A|B)是在B发生的条件下的A发生的概率。这在贝叶斯中被称为”后验概率“。即事件B发生后，重新评估事件A发生的概率。这也是朴素贝叶斯能做预测的原理。

P(A)，P(B)是先验概率，即人为经验提供的概率，比如基于大规模统计得到的概率，或者根据具体古典概型问题计算的概率。

贝叶斯公式大概是干这个用的：你在盒子里放了若干个黑球和白球，这个时候你一把抓出来几个球，结果全是黑的，这个时候你会不会凭直觉认为盒子里黑球比白球多一些？你再抓一大把，结果还全是黑的，你会不会觉得盒子里黑球比白球多很多很多？贝叶斯公式，就是把你的直觉定量化计算。

贝叶斯经典例题是假阳性问题，假设某种疾病的人群发病率为0.001，现有一种检测试剂在一个人得病的情况下，有99%的几率呈现为阳性，而在人没有得病的情况下，它仍有5%的几率呈现为阳性。那么这种检测方法是否能用于人群疾病普查呢？

要解决这个问题，我们计算一下，假如有一个人的结果为阳性，那么他的得病概率是多少呢？

设事件A表示为得病的概率，即，再设事件B为试剂结果为阳性的概率，我们瞎想得到条件概率，即后验概率。

P(A|B)=P(B|A)P(A)/P(B)=0.99×0.001/(0.99×0.001+0.05×0.999)≈0.02

注意这里的P(B)是利用全概空间计算得到的。B是阳性的概率，所有阳性的可能是：患病且阳性，不患病且阳性，因此P(B)=P(A)×0.99+(1-P(A))×0.05

得到结果：一个病人的试剂结果为阳性，他的患病概率也只有约2%。也就是说，这种方法不适用于大规模疾病普查。

朴素贝叶斯方法就是基于贝叶斯公式。大概是这样：你给定一组数据，根据数据分布算出先验概率和条件分布概率。朴素贝叶斯法通过训练数据集学习联合概率分布，也就是学习以下先验概率分布及条件概率分布：

先验分布:

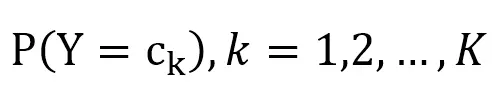
先验概率

条件概率分布：

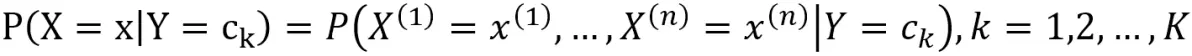
条件概率

我们注意到，交叉项概率是随着参数的增多以指数形式增长的，为了避免概率项过多，朴素贝叶斯对条件概率分布做了条件独立性假设。

即：

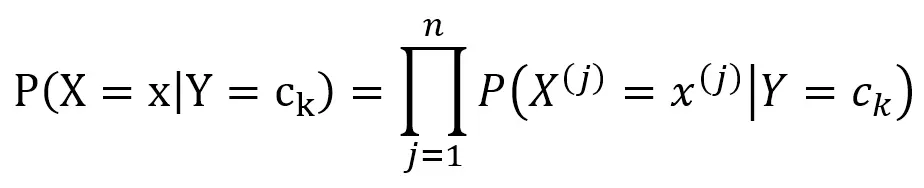
因此联合分布就变成了各自的概率相乘。

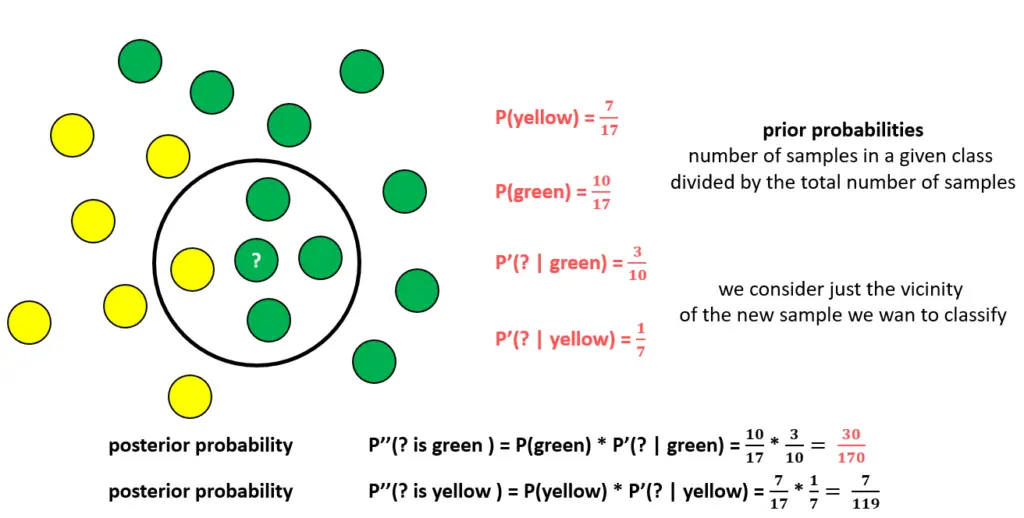
下面展示一下朴素贝叶斯分类原理：

首先计算每一类的概率，这就是我们训练好的模型参数

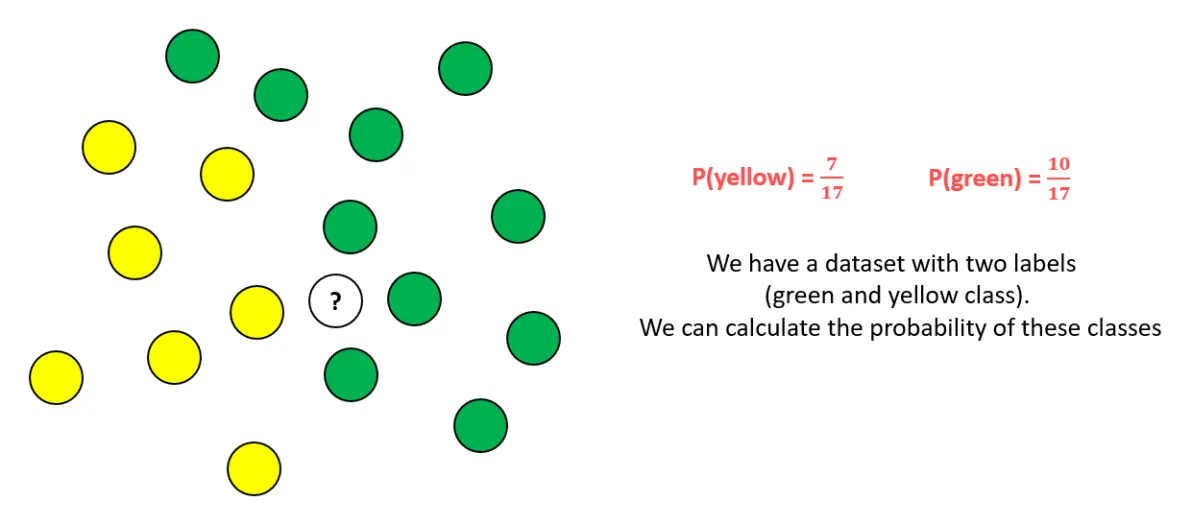
然后对于新的点，我们利用贝叶斯公式计算发现，在邻域是绿色的情况下其为绿色的概率更大，因此判断它是绿色的。

如果数据不是像上面那样，而是一个连续变化的值，这种情况如何算概率呢？这种情况，我们假设数据满足正态分布，我们就可以用数据计算正态分布的均值和方差，进而得到概率密度函数，我们就可以用这个概率密度函数去算每一个位置的概率了。

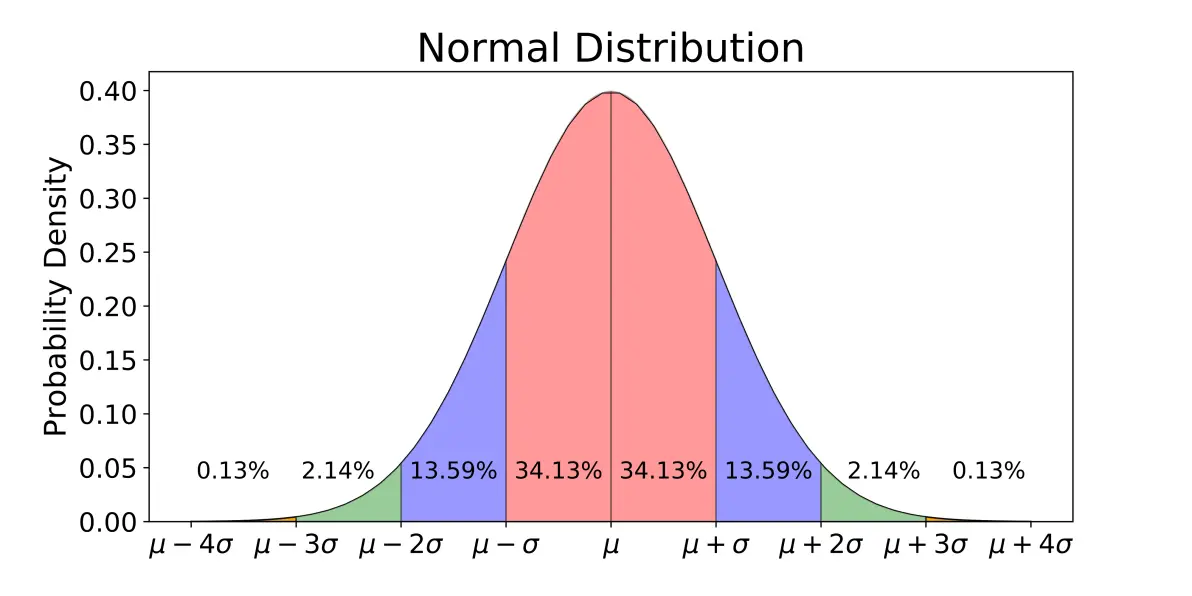
normal distribution

好了，最后还是说一下MATLAB实现方法：

创建贝叶斯模型：fitcnb

测试性能：loss

拿MATLAB说明文档的例子来说吧：

用朴素贝叶斯分类垃圾邮件：

1.Create Training Data 创建训练集

Suppose you observed 1000 emails and classified them as spam or not spam. Do this by randomly assigning -1 or 1 to y for each email.

n = 1000;                       % Sample size

rng(1);                         % For reproducibility

Y = randsample([-1 1],n,true);  % Random labels

2.特征描述

假设邮件内的信息只包含20个字母，且只由5个字母租车给，而垃圾邮件和非垃圾邮件的字母出现概率不同。

tokenProbs = [0.2 0.3 0.1 0.15 0.25;...   

0.4 0.1 0.3 0.05 0.15];             % Token relative frequencies  

tokensPerEmail = 20;                    % Fixed for convenience

X = zeros(n,5); 

X(Y == 1,:) = mnrnd(tokensPerEmail,tokenProbs(1,:),sum(Y == 1)); 

X(Y == -1,:) = mnrnd(tokensPerEmail,tokenProbs(2,:),sum(Y == -1));

3.模型训练

Mdl = fitcnb(X,Y,'DistributionNames','mn');

4.性能测试

isGenRate = resubLoss(Mdl,'LossFun','ClassifErr')

5.生成测试集

newN = 500; 

newY = randsample([-1 1],newN,true); 

newX = zeros(newN,5); 

newX(newY == 1,:) = mnrnd(tokensPerEmail,tokenProbs(1,:),...    sum(newY == 1)); newX(newY == -1,:) = mnrnd(tokensPerEmail,tokenProbs(2,:),...    sum(newY == -1));

6.测试对测试集识别率

oosGenRate = loss(Mdl,newX,newY)

模型的计算只需要一行代码：Model1=fitcnb(X,Y);是不是很简单!

参考资料：

1.MATLAB说明文档：https://ww2.mathworks.cn/help/stats/classification-naive-bayes.html

2.维基百科

3.《统计学习方法》(李航)