近期有一些小伙伴咨询我六西格玛黑带考试相关的问题,我觉得有些题目比较具有代表性,因而会选择性发一些我个人的看法在专栏里面,希望大家喜欢和支持。

对于具有3σ控制限的Xbar-R图来说,原来子组样本含量为3,后来重新设计控制图,子组样本量为5,将会导致什么样的结果:C
A. 增加第I类错误风险,同时降低第11类错误风险
B. 增加第II类错误风险,同时降低第I类错误风险
C. 降低第II类错误风险,第I类错误风险不变
D. 降低第I类错误风险,第11类错误风险不变
上面这个题目实际可以秒杀,因为只是样本量变了,但是3σ控制限以内是99.73%是固定的,不会变,另外上面的题目已经提到了,控制图重新设计了,也就是说σ变了,具体变大变小实际不用考虑,因为控制限是根据σ换算来的,那么3σ控制限外面的概率也就是α(I类错误风险)那么就是1-99.73%=0.27%,不会变,所以选择C即可。

让我们继续进行分析,上面说到σ会变化,根据中心极限定理,σ应该会变小,那么据样本量功效公式,可知:
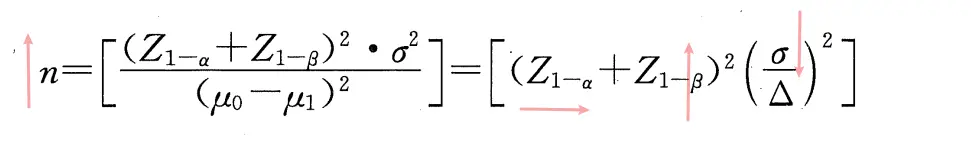
样本量功效公式
其中n变大,α风险不变,那么Z(1-a)大小不变,σ变小,那么Z(1-β)必然变大,那么功效:1-β必然是变大的,β风险也就是第II类错误风险必然变小。
下面通过一些图来具体说明一下:
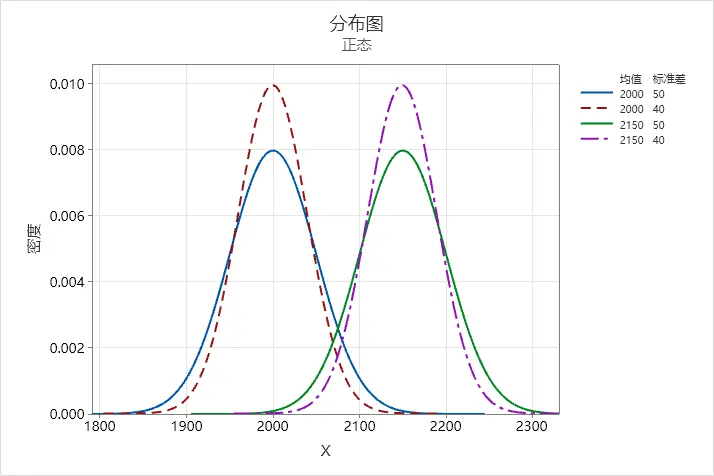
概率分布图
由于σ变小,那么整个分布按照正态分布的特点,会变得区域扁平,比如上图这里,存在两个正态分布,只是均值不一样,σ大小是一样的,标准差比较大的时候那么对应两个实线区域重叠面积会比较大,标准差比较小的时候对应两个虚线区域重叠面积会比较小。
假设靠左边的图是我们的原分布(在这个题目里面可以理解为当前研究的总体),右侧的是其它分布,a风险实际就是属于原分布但是判定为其它分布的概率,属于错判,β风险实际就是属于其它分布但是判定为原分布的概率,属于漏判。
我们再来看下面两张图:
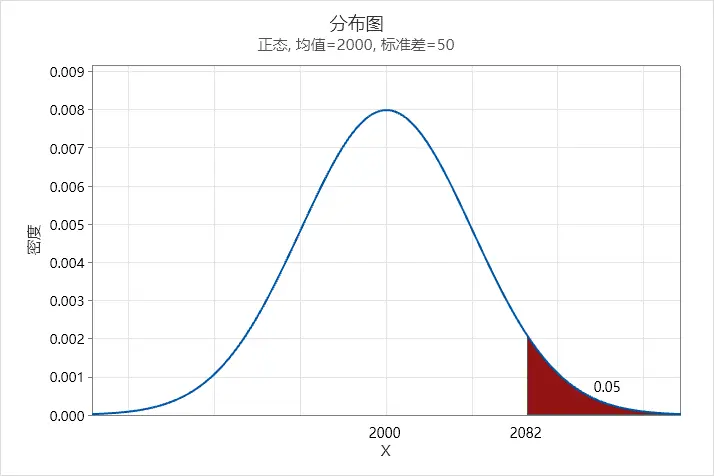
概率分布图2
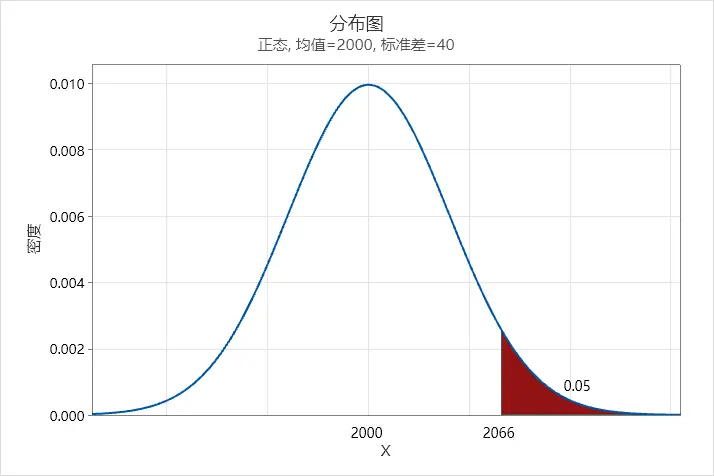
概率分布图3
上面两个图只是标准差不一样,右尾概率都是5%(一般α都默认为5%)的情况下,对应X值不一样,标准差小一点的X值会小一些,那么我们再来看六西格玛管理里面的图说明这一点:

样本功效图例
上面几张图已经说明了,标准差变化造成的影响,比如分布区域扁平,重叠面积变小,α风险对应X会变化,趋近于分布的平均值,那么对应上面这个图来看,标准差如果变小的话,图形扁平化,假定α风险大小始终不变(以上已论证),α和β风险概率区域中间这根线会往左边移动(左图原分布α风险对应X变小),β风险区域面积变小,1-β也就是所谓功效会变大。
因而可以得到结论:样本量变大的时候,功效变大,第II类风险也就是β风险会变小,这和上面的公式分析也是契合的。

样本量和功效以前出过视频有讲过,当时画质比较糊,讲得不算很清楚,大家有时间可以看看,由于水平有限,难免会有错漏,还望指正。