MATLAB学习笔记：技巧与心得分享

本笔记结合以下视频使用

2023/1/21 11：20更新

p4 结构矩阵和元胞数组

元胞数组

1、什么是元胞数组？

元胞数组是MATLAB中特有的一种数据类型

元胞数组中一个元素叫做一个元胞

每一个元胞可以包含任意一种类型的数据，数据类型可以是整型数、字符串、双精度数、结构体等任意类型MATLAB所有的数据类型

每一个元胞的数据可以具有不同的大小，从单个数到N维数组均可

称这些元胞组合起来的数组为元胞数组。

2、创建元胞数组

元胞数组常见的两种创建方法

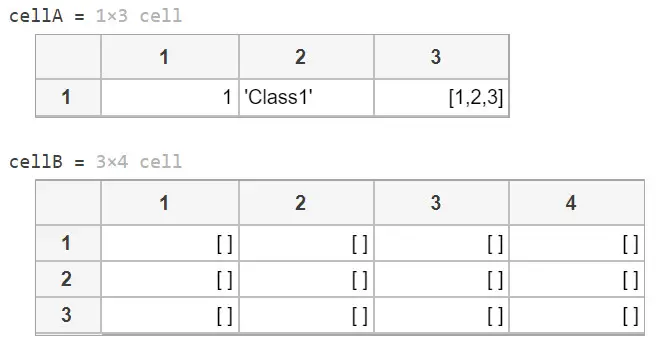
1.用花括号 { } (元胞数组构造运算符) 直接创建数组cellA

2.用cell函数来创建,cell(m,n)生成一个m行n列的空的元胞数组cellB

3、元胞数组的访问

引用元胞数组的元素有两种方法。

1.使用圆括号（）

将索引括在圆括号（）中以引用元胞集

观察上述图片可知，使用圆括号（）索引时，虽然里面包含数据类型和大小均不同，但“ans”显示的结果均为1x1 cell 数组，又或者访问第二行一整行，显示结果为1x3 cell，cell即上文提到的元胞，故将索引括在圆括号（）中以引用元胞集

2.使用花括号 { }

将索引括在花括号 { } 中以引用各个元胞中的文本、数字或其他数据。

观察上述图片，使用花括号 { } 索引时，结果显示为元胞中的内容，数据类型也各有不同，而不是统一的cell

当使用花括号进行索引来访问多个元胞的内容时，MATLAB会以逗号分隔的列表形式返回这些元胞的内容。

因为每个元胞可以包含不同类型的数据，所以无法将此列表分配给单个变量。但是，可以将此列表分配给与元胞数量相同的变量。MATLAB将按列顺序赋给变量。

[A,B,C]=cellA{2,1:3}

如果每个元胞都包含相同类型的数据，则可以通过将数组串联运算符应用于逗号分隔的列表来创建单个变量。

num = [ cellA {1,3} ]

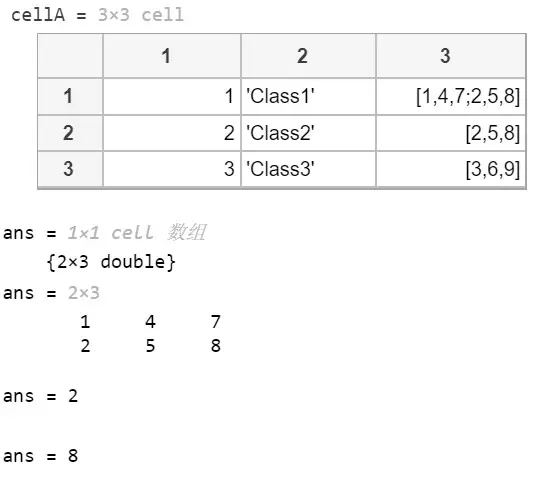
4、访问部分元胞的多级索引

访问存储于元胞数组的元胞中的数组数据的方法

结构体数组

1、什么是结构体数组？

结构体数组是使用名为“字段”的数据容器将相关数据组合在一起的数据类型。

即把不同数据类型的变量放到同一个变量名下，通过指定的名称访问

每个字段都可以包含任意类型的数据。

2、结构体的创建

结构体的创建常见的也有两种方法

1.使用圆点表示法创建、分配和访问结构体字段中的数据。

2.使用函数创建一个结构体数组

s = struct(field1,value1,...,fieldN,valueN)

其中field是字段，使用格式必须为：'string'，value为值

结果同上

3、访问字段中的值

创建字段后，使用圆点表示法来访问和更改它存储的值：变量名.字段

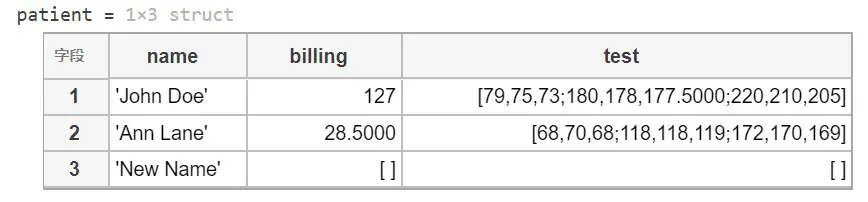
如： patient.billing = 512.00

4、对非标量结构体数组进行索引

结构体数组可以是非标量的。可以创建任意大小的结构体数组，只要数组中的每个结构体都有相同的字段即可。

当将多个结构体存储为一个结构体数组时，可以使用数组索引和圆点表示法来访问单个结构体及其字段。

例如，向添加第二个结构体，其中包含第二个患者的有关数据。此外，将原始值赋给第一个结构体的字段。由于该数组现在有两个结构体，必须通过索引来访问第一个结构体，如所示。

如果向数组中添加新结构体而未指定其所有字段，则未指定的字段包含空数组。

结构体数组具有下列属性：

数组中的所有结构体都具有相同数目的字段。
所有结构体都具有相同的字段名称。
不同结构体中的同名字段可包含不同类型或大小的数据。

注意

仅当引用结构体数组的单个元素时，才能为字段的部分内容建立索引。

MATLAB 不支持诸如的语句

后者尝试为结构体数组的多个元素的字段建立索引。请改用函数。

2023/1/22 13：30更新

（矩阵部分例子过多且视频讲解详细，故省略示例的演示，只在视频原文的基础上给出函数用法和保留部分示例代码，另线代知识部分只保留视频中出现的文字部分，不给出更多扩展内容）

p5 通用矩阵与常见特殊矩阵

1、特殊矩阵

-通用特殊矩阵

零矩阵：zeros

幺矩阵：ones

单位矩阵：eye

（I = eye(n,m) 生成主对角线元素为 1，其他位置元素为 0 的 n×m 矩阵。）

区间 (0,1) 内均匀分布的随机数矩阵：rand

正态分布的随机数矩阵：randn

ex1：

建立[20,50]内均匀分布的5阶随机矩阵

公式：y = a + (b-a) x

exA1 = 20 +30*rand(5)

ex2：

产生一个均值为0.6，方差为0.1的4阶正态分布随机矩阵

公式：y = μ + σx

exA2 = 0.6 + sqrt(0.1)*randn(4)

-用于特殊领域的矩阵

% % 魔方矩阵范德蒙矩阵希尔伯特矩阵

幻（魔）方矩阵：magic

M = magic(n)

由 1 到 n2 的整数构成

各行，各列，主对角线均相等且为n(n^2+1)/2的 n×n 矩阵

n 的阶数必须是大于或等于 3 的标量才能创建有效的幻方矩阵。

范德蒙矩阵：vander

A = vander(v)

返回 Vandermonde 矩阵以使其列是向量 v 的幂。

任意子方阵可逆

希尔伯特矩阵: hilb 高度病态病态程度与阶数有关 hi,j = 1/(i + j -1)

H = hilb(n)

返回阶数为 n 的 Hilbert 矩阵。

Hilbert 矩阵是病态矩阵的典型示例

p6 矩阵变换

复习线代（一些名词的回忆）

对角阵、数量矩阵、单位阵，秩、迹、逆(伪逆)、行列式、条件数

范数（norm）：简单来说，用来度量某个向量空间（或矩阵）中的每个向量的长度或大小。

一些性质：转置运算对角线元素不变，矩阵的秩（rank）与方程组求解、判断是否可逆有关，矩

阵的迹（trace）为矩阵主对角线元素之和，相似变换时矩阵的迹不变。

-对角阵与三角阵

diag：创建对角矩阵或获取矩阵的对角元素

D = diag(v) 返回包含主对角线上向量 v 的元素的对角矩阵。

D = diag(v,k) 将向量 v 的元素放置在第 k 条对角线上。k=0 表示主对角线，k>0 位于主对角线上方，k<0 位于主对角线下方。

x = diag(A) 返回 A 的主对角线元素的列向量。

x = diag(A,k) 返回 A 的第 k 条对角线上元素的列向量。

数量矩阵

在eye的基础上乘以数得到

B = eye(4)

DB = 7*B

ex1：建立一个5x5的矩阵A1，将A1的第一行元素乘1，第二行元素乘2，....，第五行元素乘5.

A1 = magic(5)

D1 = diag(1:5)

A1ans = D1*A1

ex1+：建立一个4x4的矩阵A2，将A2的第一列元素乘1，第二列元素乘2，....，第四列元素乘4.

A2 = magic(4)

D2 = diag(1:4)

A2ans = A2*D2

三角阵：

上三角 (triu)

U = triu(A,k) 返回位于 A 的第 k 条对角线上以及该对角线上方的元素。

下三角 (tril)

L = tril(A,k) 返回 A 的第 k 个对角线上以及该对角线下方的元素。

小三角

改变上述函数tril和triu中的k值即可

-矩阵的转置与旋转

转置：

B = A.' 返回 A 的非共轭转置，即每个元素的行和列索引都会互换。

如果 A 包含复数元素，则 A.' 不会影响虚部符号。

例如，如果 A(3,2) 是 1+2i 且 B = A.'，则元素 B(2,3) 也是 1+2i。

共轭转置：

B = A' 计算 A 的复共轭转置。

即 A(3,2) 是 1+2i 且 B = A'，则元素 B(2,3) 是 1-2i。

旋转：

B = rot90(A,k) 将数组 A 按逆时针方向旋转 k*90 度，其中 k 是一个整数。

左右翻转：

B = fliplr(A) 返回 A，围绕垂直轴按左右方向翻转其各列。

如果 A 是一个行向量，则 fliplr(A) 返回一个相同长度的向量，其元素的顺序颠倒。如果 A 是一个列向量，则 fliplr(A) 只返回 A。对于多维数组，fliplr 作用于由第一个和第二个维度构成的平面。

上下翻转：

B = flipud(A) 返回 A，围绕水平轴按上下方向翻转其各行。

如果 A 是一个列向量，则 flipud(A) 返回一个相同长度的向量，其元素的顺序颠倒。如果 A 是一个行向量，则 flipud(A) 只返回 A。对于多维数组，flipud 作用于由第一个和第二个维度构成的平面。

-矩阵的逆与广义逆（伪逆）

矩阵的逆：对于一个方阵A，如果存在一个与其同阶的方阵B，使得

A*B = B*A = I

则称B与A互为逆矩阵

Y = inv(X) 计算方阵 X 的逆矩阵。

-X^(-1) 等效于 inv(X)。

-x = A\b 的计算方式与 x = inv(A)*b 不同，建议用于求解线性方程组。

代码解释：

E = magic(3);

Einv = inv(E)

res = E*Einv

应用：

求解线性方程组 Ax = b

x = A^-1*b

ex2：求解下列方程组

x+2y+3z=5

x+4y+9z=-2

x+8y+27z=6

解：

A = [1 2 3;1 4 9;1 8 27]

b = [5;-2;6]

x = inv(A)*b

伪逆 pinv()

B = pinv(A) 返回矩阵的 Moore-Penrose 伪逆。

B = pinv(A,tol) 指定容差的值。将中小于容差的奇异值视为零。

对于非方阵、奇异阵（是方阵，但行列式为0）

或非满秩矩阵（rank(A) ~= n ）

Aex2 = [3 1 1 1;1 3 1 1;1 1 3 1]

rank(Aex2) %行满秩

A2ans = pinv(Aex2)

Aex2*A2ans

p7 矩阵求值（行列式秩迹范数条件数特征值特征向量）

写在前面：矩阵变换矩阵 -> 矩阵

矩阵求值矩阵 -> 数值

包括：行列式求值、矩阵的秩、矩阵的迹、范数、条件数

-方阵的行列式 (de'terminant)

% 注意：方阵才有行列式

d = det(A) 返回方阵 A 的行列式。

-矩阵的秩与迹

秩：非零子式的最高阶数 rank

秩的另一种解释：将矩阵按列分解为个向量，组成一个向量组。

则该向量组的一个最大线性无关组中包含向量的个数称为矩阵的行秩。同理可定义列秩，可证列秩=行秩=秩

应用：

% -是否可逆

% -初等变换后矩阵的秩不变

% -判断非齐次线性方程组解的情况

迹: 矩阵主对角线元素的和 trace

矩阵的秩

k = rank(A) 返回矩阵 A 的秩。

矩阵的迹

b = trace(A) 计算矩阵 A 的对角线元素之和

-向量和矩阵的范数

% 向量或矩阵的范数用来度量其在某种意义下的长度。有多种定义，定义不同值也不同。

% 求范数时，注意要弄清楚是哪一种

% 向量的范数

V = [1 2 3 4]

norm(V,1) % 向量-1 范数元素绝对值之和

norm(V,2) % 向量-2 范数元素平方和的平方根

norm(V,inf) % 向量-∞ 范数所有向量元素绝对值中的最大值

% 矩阵的范数

E = magic(4)

norm(E,1) % 矩阵-1 范数所有矩阵列元素绝对值之和的最大值

norm(E,2) % 矩阵-2 范数矩阵的最大特征值的平方根

norm(E,inf) % 矩阵-∞ 范数所有矩阵行元素绝对值之和的最大值

-矩阵的条件数（工程中应用非常广泛）

% 在求解线性方程组Ax = b时，考虑摄动对解向量的影响程度，影响大则称为病态矩阵，反之为良性矩阵。

% 引入条件数，用来描述病态或良性的程度，属于矩阵的属性

% 定义矩阵A的条件数为矩阵A的范数与矩阵A的逆的范数的乘积，条件数一定大于1，越接近于1越好，即越良性。

F = rand(4)

F1 = hilb(4)

cond(F,1) % 1-范数下的条件数

cond(F,2) % 2-范数下的条件数

cond(F,inf) % ∞-范数下的条件数

% 希尔伯特 -高度病态矩阵

cond(F1,1) % 1-范数下的条件数

cond(F1,2) % 2-范数下的条件数

cond(F1,inf) % ∞-范数下的条件数

-矩阵特征值与特征向量（工程中应用非常广泛）

对于n阶方阵A，求数 λ 和向量 ξ，使得 A*ξ = λ*ξ ，则 λ 为A的特征值，ξ 为特征向量

即求解方程 A*ξ = λ*ξ ，变形后得到（ A-λ*I )*ξ = 0 ，若使该方程有非零解ξ，则需其系数行列式为0

即 | A-λ*I |= 0

该式是一个关于 λ 的 n次多项式，其解含有 n个根，即矩阵 A的 n个特征值，每个特征值对应无穷多个特征向量。

-特征值与特征向量的求解

e = eig(A) 返回一个列向量，其中包含方阵 A 的特征值。

[V,D] = eig(A) 返回A的全部特征值构成的对角矩阵 D 和矩阵 V，其各列是对应的右特征向量，使得 A*V = V*D。

注意：一个矩阵的特征向量含有无穷多个，eig函数只找出其中n个，

但A的其他特征向量均可由这n个特征向量的线性组合表示出来

p8 稀疏矩阵与稀疏储存方式

-稀疏矩阵

知识回顾：转置

两种转置矩阵：X.' 和 X'

-区分：稀疏矩阵和采用稀疏方式存储的矩阵

为什么要采用稀疏存储方式？节省空间

% 稀疏矩阵

A1 = [2 0 0 0;

0 0 0 0;

0 -5 0 0;

3 0 0 0 ];

% 采用稀疏方式存储的矩阵

A1 = [2 0 0 0;

0 0 0 0;

0 -5 0 0;

3 0 0 0 ]

% 普通方式存储 2 0 0 3 0 0 -5 0 0 0 0 0 0 0 0 0

% 稀疏方式存储 (1,1),2,(4,1),3,(3,2),-5

-稀疏存储方式的产生 sparse( )

S = sparse(A)

通过挤出任何零元素将满矩阵转换为稀疏格式。

如果矩阵包含许多零，将矩阵转换为稀疏存储空间可以节省内存。

S = sparse(m,n) 生成 m×n 全零稀疏矩阵

S1 = sparse(u,v,S)

根据 u、v 和 S 三元组生成稀疏矩阵 S1，以使 S1(u(k),v(k)) = S(k)。

max(u)×max(v) 输出矩阵为 length(S) 个非零值元素分配了空间。

如果输入 u、v 和 S 为向量或矩阵，则它们必须具有相同数量的元素。

% ex

u = [1 3 5 2];

v = [1 2 2 4] ;

S = [-5 24 9 17];

S3 = sparse(u,v,S)

full(S3);

-与稀疏矩阵操作有关的函数

[u,v,S] = find(A) 返回矩阵A中非零元素的下标和元素

A = full(S) 返回稀疏存储矩阵S的完全存储方式 full<->sparse

spconvert ( ) 便捷创建一个稀疏存储矩阵

S = spconvert(D) 根据 D 的列，按与 sparse 函数类似的方式构造稀疏矩阵 S。

·如果 D 的大小为 N×3，则 spconvert 将使用 D 的列 [i,j,re] 构造 S，以使 S(i(k), j(k)) = re(k)。

% ex1：

A2 = [ 2 2 1 ;

3 1 -1 ;

4 3 3 ;

5 3 8 ;

6 6 12 ; ]

S4 = spconvert(A2)

full(S4);

% 注意A2并非稀疏存储矩阵，S4才是，A2只是作为spconvert函数的参数方便去产生稀疏矩阵

spdiags ( ) 创建对角稀疏矩阵梳状稀疏矩阵

S = spdiags(Bin,d,m,n) 通过获取 Bin 的列并沿 d 指定的对角线放置它们，来创建一个 m×n 稀疏矩阵 S。

%ex

B = [0 1 4 9 0;

4 7 9 0 3;

0 2 6 4 9]

Bz = B.'

d = [-1,0,2].'

full(spdiags(Bz,d,5,5))

-稀疏矩阵应用举例

-求解下列三对角线性方程组的解

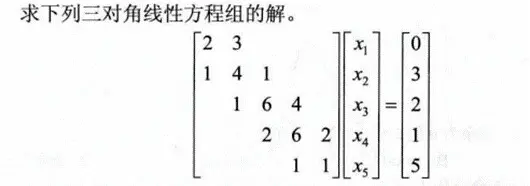
分析：左侧系数矩阵是一个稀疏矩阵，只有三条对角线上有元素

% tips:当参与运算的矩阵不全是稀疏矩阵时，运算结果一般为完全存储方式

% ex2:

C1 = [1 1 2 1 0;2 4 6 6 1;0 3 1 4 2].'

d1 = [-1 0 1].'

C = full(spdiags(C1,d1,5,5))

V2 = [0 3 2 1 5].'

% Ax = b

% 即 x = A^-1*b

x = (inv(C)*V2).'

返回上级列表

请

联系我们

，获取更多内容

< 上一篇: MATLAB App与GUI：未来发展趋势探讨

下一篇: MATLAB数值分析：二分法求根实例 >