模拟IC设计中的失配：改善原则与方法（一）

本文主要介绍了失配(mismatch)的产生以及改善失配的通用设计原则，至于失配对电路性能的影响，如失调电压以及CMRR和PSRR将会后续在另外开文章详细分析。

失配的产生

实际芯片在生产制造过程中由于每个加工步骤的不确定性会使得名义上的设计值与最终物理实现值并不相同。这种生产不确定性导致的绝对偏差值可能高达20%，且每个元件具体的偏差程度是无法预测的，因而电路的性能如果仅取决于单个器件的参数值，则最终电路实际表现出的性能可能与预期设计值发生显著偏离。区别于绝对偏差，在一次制造过程中同类型元件参数值的偏差称之为相对偏差，相对偏差通过合理的设计和版图布局可以使其不匹配的程度达到1% ~ 0.1%。这也是为什么实际电路设计时，通常希望电路的性能参数取决于器件参数的比值而不是单个器件参数的绝对值（注意一定得是同类型元件参数的比值，例如基于电阻比确定反馈放大器的增益，所选用的电阻类型要保持一致）。通常失配指的是同一块芯片上两个相同类型器件间参数的相对偏差而非单个器件参数值的绝对偏差。

改善失配的通用设计原则

为了尽可能减小同类型器件的不匹配程度以让最终物理所实现的电路性能接近理想设计值，需要按照一定的匹配原则进行电路设计。

对于工作在饱和区的MOS管，其I-V一阶关系表达式如下

因而对于MOS管来说，其失配因素可以包括μ、Cox、W、L和VTH多个参数之间的不匹配。最终会导致两个标称相同晶体管的漏极电流ID（对于给定的栅源电压）或栅源电压VGS（对于给定的漏极电流）之间的不匹配。

考虑到对于设计者来说，在MOS管设计中一般可调节的参数为W、L、ID和VGS，其中W、L这两个尺寸参数的选择决定了最终MOS管物理版图的实现。一般来说器件的尺寸W、L越大，MOS管各种参数的随机不匹配性会经历更大程度的平均，因而可以预期得到的失配相对值越小。也即W、L越大，ΔW/W、ΔL/L、Δμ/μ、ΔCox/Cox越小。

例如一个管子的宽长比为W/L0，而另一个管子的宽长比是W/(n*L0)，其可以认为是n个(W/L0)的管子源漏串联形成（忽略二阶效应），其等效后Leq对应的失配是n个管子L0失配的均方根值

因而n个管子串联后，其L的失配值相较原来单个管子小了√n倍。其他参数也可以进行类似的分析，因为更大尺寸的管子可以视作许多小管子的串并联，故不匹配性被平均进而缩小。定量上可以得到MOS管参数失配的标准偏差是

接下来对模拟设计中最常用的电流镜模块进行分析。

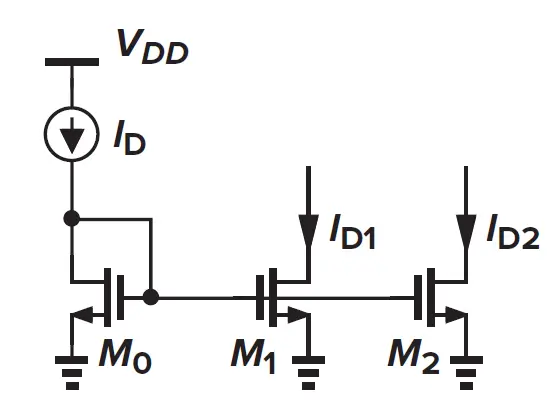
简单电流镜

如果希望ID1 = N * ID，从I-V关系可知需要

这里实际上有4个设计参数可以供设计者选择，但是为了改善匹配性，一般设计中会使用单位匹配原则进行设计，也即所有器件都是基于单位器件串并联形成。这样的好处可以从两方面来分析，一是如上文所提到的，器件的失配程度实际上取决于器件的面积，使用单位器件构成最终设计，可以使得每个单元的不匹配程度类似；第二点更为重要是，由于物理实现的构造只有采用单位器件才能真正实现设计时所指定的比例关系，如下图所示一个1 : 2的电流镜，如果设计时维持镜像管L不变W翻倍，则由于制造过程Gate Corner的不确定（W1 = WREF + ΔW1），设计参数中W的翻倍（W2 = 2WREF +ΔW2）并不等价于实际宽度的翻倍（ΔW2 不一定=2*ΔW2，故W2 ≠ 2*W1）。为此更合理的方式应是如下图(c)所示，采用单位器件的方式进行比例缩放。

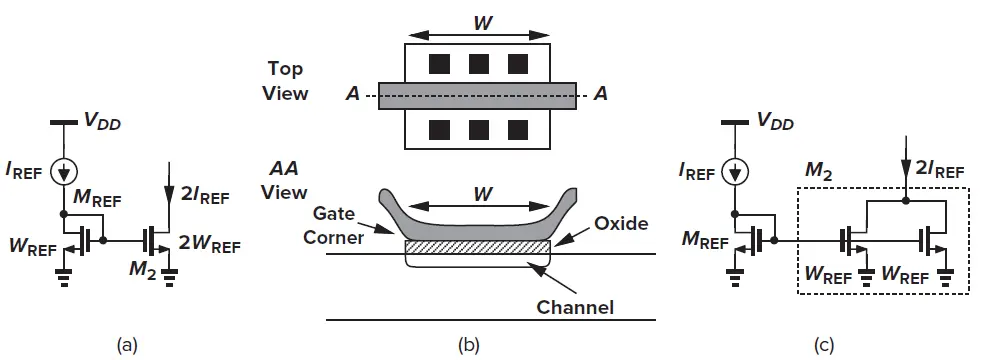
单位匹配原则[1]

注意设计中在MOS管参数选择上为了实现真正意义上的单位匹配原则，应是在W, L, Fingers都相同的情况下去改变Multiplier。

cadence schematic中修改晶体管的属性

而不是仅保证W, L相同的情况下去改变Fingers以实现对应的比例关系。下图是1 : 5电流镜物理版图不同实现方式的对比，(a)图是以5个Fingers方式形成镜像晶体管（Fingers即叉指结构），(b)图是以5个Multiplier方式形成镜像晶体管（Multiplier才是真正的并联结构）。可以看到Fingers实际是以合并扩散区的方式进行物理实现，从而减小了所需的面积，但也正因如此其源、漏面积不再是被镜像晶体管的5倍，最终对应的寄生电容和电阻也就不满足比例关系。

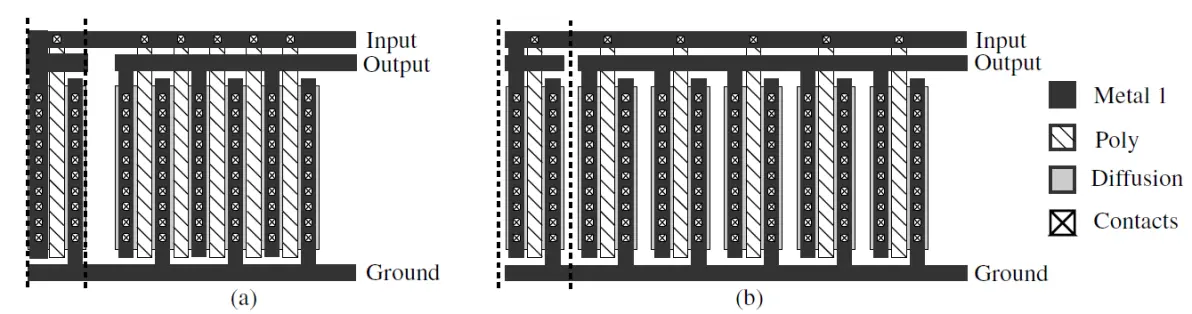
1:5 电流镜版图的两者实现方式[2]

而且考虑到倾斜注入（如下图所示）以及STI应力效应，Fingers方式最终表现出的匹配特性也不如以Multiplier方式所实现的电流镜好（Multiplier保证每个管子均经受相同的倾斜注入以及STI应力效应的影响）

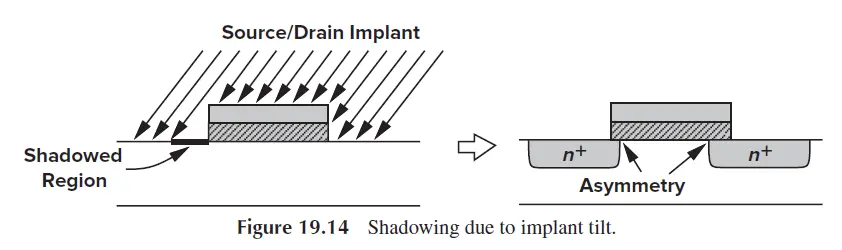
倾斜注入造成栅阴影区引发源漏边缘扩散不对称[1]

对于电阻的实现也是同理，除了电阻自身也即下图中酒红色长条本体贡献阻抗外，电阻两端的通孔也会贡献阻抗。为了得到更精确的比例关系，应该采用单位器件组合的方式实现去实现。从而保证不仅主体酒红色长条长度满足比例关系，过孔数量也满足设计所需的比例关系。

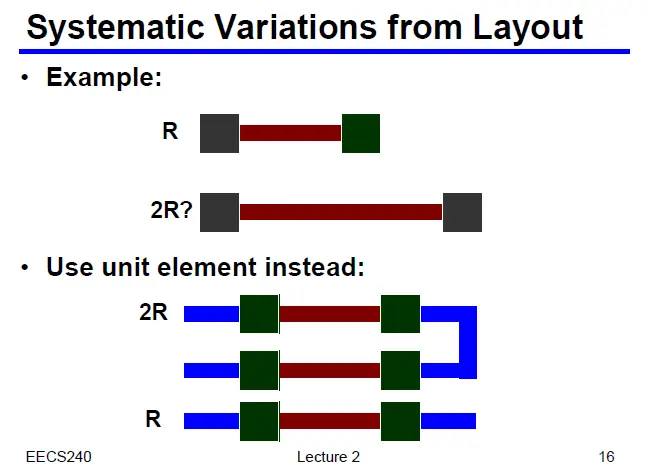
电阻比例的实现[3]

在电路版图实现上除了采用单位匹配原则保证器件自身的匹配外，还需要尽可能保证匹配器件周围环境的相同。如下图所示是一个1:1的电流镜，可以看到M1管源端右侧看到的是M2管的漏端即有源区，而M2管右侧却是场氧化物，这显然与M1管源端所处环境不同。两个管子的漏端也同理。

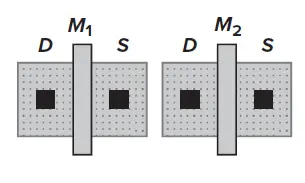
1 : 1电流镜平移对称布局(避免倾向注入影响)[1]

如下图所示，为了改善这种不匹配，实际实现时通常会在匹配器件周围加dummy器件以保证环境的一致性。

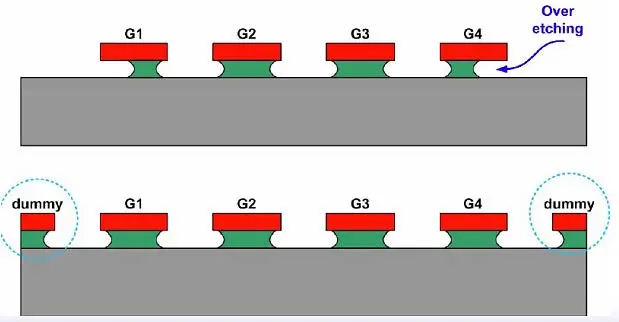
Dummy器件

在匹配器件周围也尽可能避免走一些无关的连接线，如一定要走则也需要加上dummy连接线保证匹配。

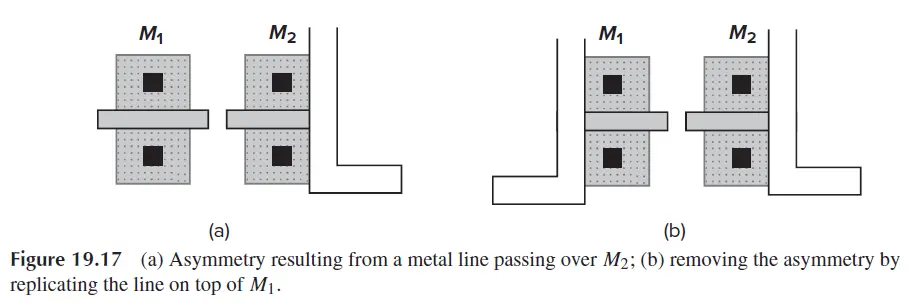
Dummy连接线[1]

此外制造过程中器件的参数可能会发生梯度偏移现象，如下图所示。

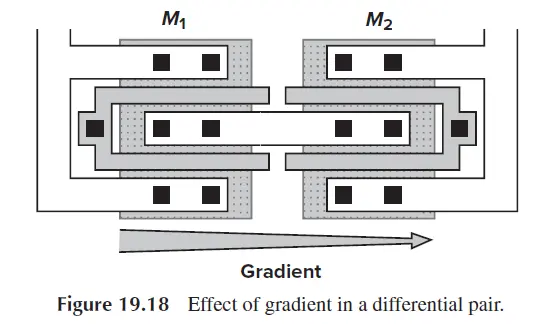
梯度效应[1]

如下图所示，工艺相关的梯度效应可以通过共质心布局缓解。在几何意义上，每个器件的质心都位于结构的中心。由于任何梯度都可以分解为水平和垂直分量，因此共质心布局克服了任何方向的线性梯度偏移影响。

共质心布局[1]

但这样摆放后，会导致后续布线困难，特别是考虑到希望匹配器件周围的环境保持一致从而避免寄生的不对称性。一个差分输入对含布线的简化版图如下图所示，考虑到差分对的栅端作为放大器的输入端是一个敏感结点，因而重点观察此版图为了保证布线对称平衡对栅端的寄生影响。此处将源端连接线跨越了栅极连线并且并排走线，从而引起源端到放大器输入端的寄生电容。考虑到这些寄生电容无法做到完全匹配，可能会将源端上的扰动经由这种不匹配在放大器输入端转化成差模干扰影响原有信号放大。所以通常来说，避免对敏感结点的寄生是更优的布局布线思路，在无法避免寄生产生的场合则应尽可能保证互连平衡。不过实际上考虑到此处放大器的栅源两端由于器件自身就已经贡献了大量栅源电容CGS，此处互连线导致的额外CGS,par影响不会那么显著(因为CGS > CGS,par，栅源不匹配主要取决于器件自身CGS的不匹配)，但如果此处到栅端的额外寄生是从其他结点耦合过来则需要仔细分析是否会造成影响。

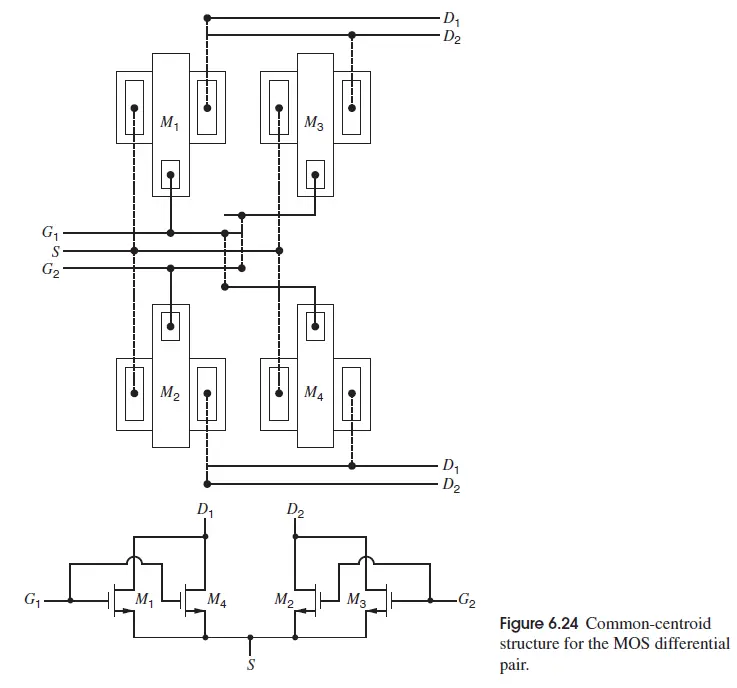
差分对共质心版图[4]

另外上述共质心版图为了连接交叉器件增大了匹配器件的距离，这在工艺梯度不是影响失配的主要因素时甚至会使得器件匹配变得更差。在版图设计时，也可以考虑采用一维交叉耦合的方式去避免线性梯度效应，其实现方式大致可以分为ABBA和ABAB，如下图所示。一般来说ABBA可以实现更好的梯度效应抑制，但B器件的周围环境明显与A器件周围的环境不同，因而ABBA中需要在两边引入dummy器件保证环境匹配。

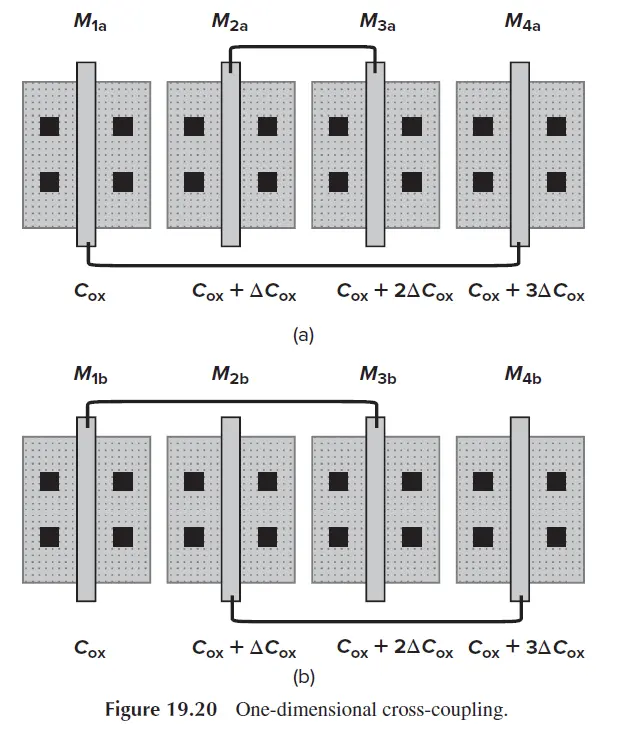
一维交叉耦合(只考虑栅极布线)[1]

以上简单介绍了改善失配最主要的通用设计原则。在此简单做一个总结：

1. 电路性能指标最好依赖于器件参数的比值而不是单个器件参数的绝对值，且比值必须基于相同类型器件参数的比值（类似栅氧电容和结电容、poly电阻和metal电阻这种不同类型的比值不可行）
2. 比值的实现应基于相同类型器件，且采用单位匹配原则（MOS管应用Multiplier而不是Fingers去调节比例）
3. 需要匹配的器件应在物理版图上尽可能的靠近，且方向的摆放也应保持一致，核心模块可以采用共质心布局。
4. 匹配器件的周围环境应尽可能保持一致（不仅是dummy器件，可能还要考虑温度，应力等实际环境的影响），尽可能减小匹配器件周围的非必要走线，避免寄生 > 平衡寄生
5. 一般来说电阻的匹配不如电容，这也是为什么高精度ADC中更多使用电容阵列而非电阻阵列的原因之一。

因笔者水平有限，如有错误还请批评指正！

更多内容可见微信公众号/知乎：WithB

欢迎关注！

觉得有帮助的话，不妨一键三连支持一波~ 

参考文献：

[1] B. Razavi, Design of Analog CMOS Integrated Circuits. 2017.

[2] P. E. Allen and D. R. Holberg, CMOS analog circuit design. Elsevier, 2011.

[3] E. Alon. "EE240: Advanced Analog Integrated Circuits." http://bwrcs.eecs.berkeley.edu/Classes/icdesign/ee240_sp10/lectures.html (accessed.

[4] P. R. Gray, P. J. Hurst, S. H. Lewis, and R. G. Meyer, Analysis and design of analog integrated circuits. John Wiley & Sons, 2009.