前言
在以前的文章中,我曾多次对二阶系统特别是RLC电路进行计算,对RLC谐振电路熟悉的电路爱好者应该都知道在谐振时系统的电流或者电压会达到最大,但是却比较少关注元件的功率,以及RLC在串联或并联以及使用电压激励或电流激励等不同情况下的区别。
在本文中,主要计算RLC电路在RLC串联正弦电压激励、RLC并联正弦电压激励和RLC并联正弦电流激励共三种情况的稳态时,各个元件的电压U、电流I、视在功率S随频率的变化。为避免重复工作,本文在计算时会参照以前文章已经得出的结论和公式。
前文导航:
[1]:RLC串联电路电流响应:https://www.bilibili.com/read/cv13226431/
[2]:二阶常系数线性微分方程解:https://www.bilibili.com/read/cv16026431/
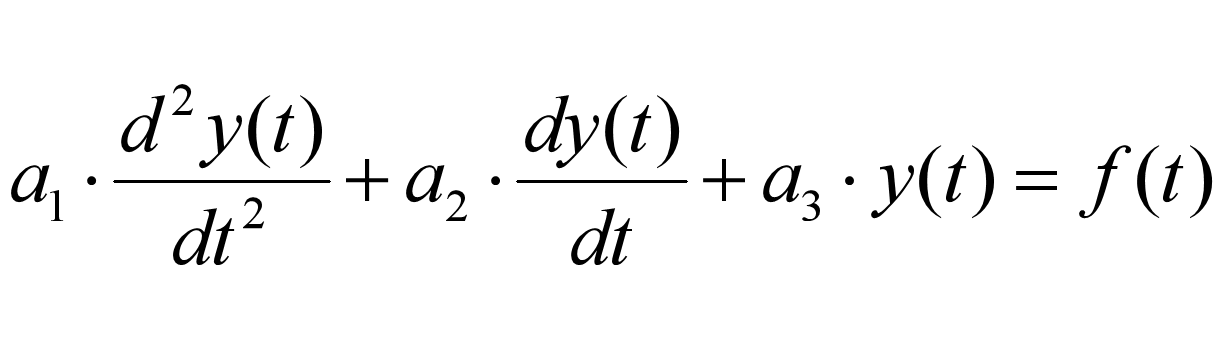

正文
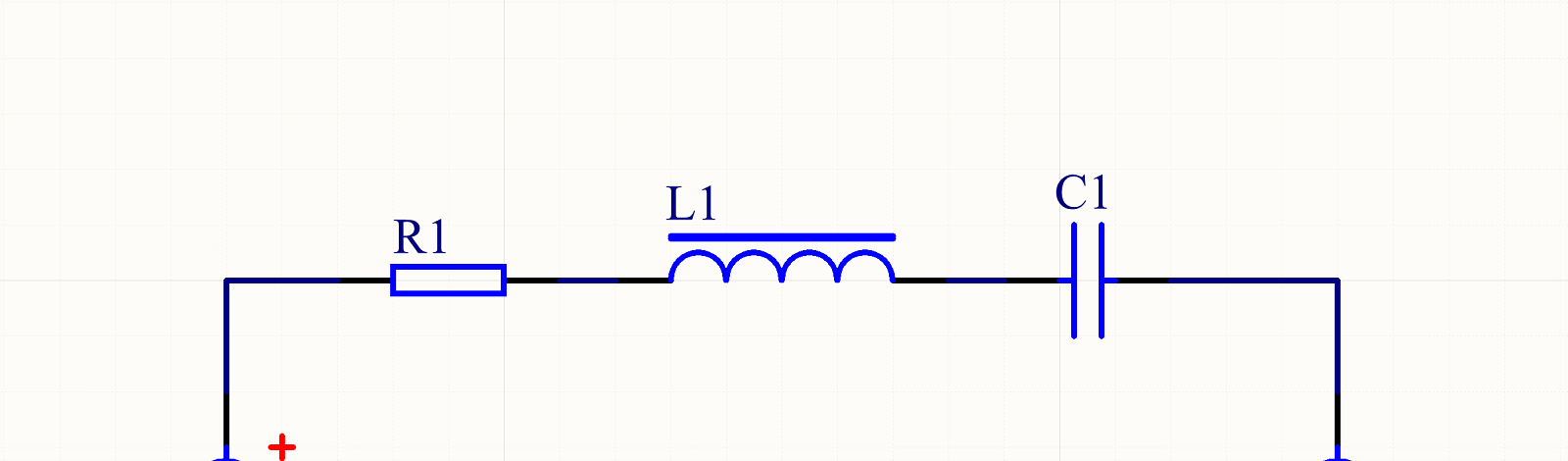
1、正弦电压源驱动的RLC串联电路
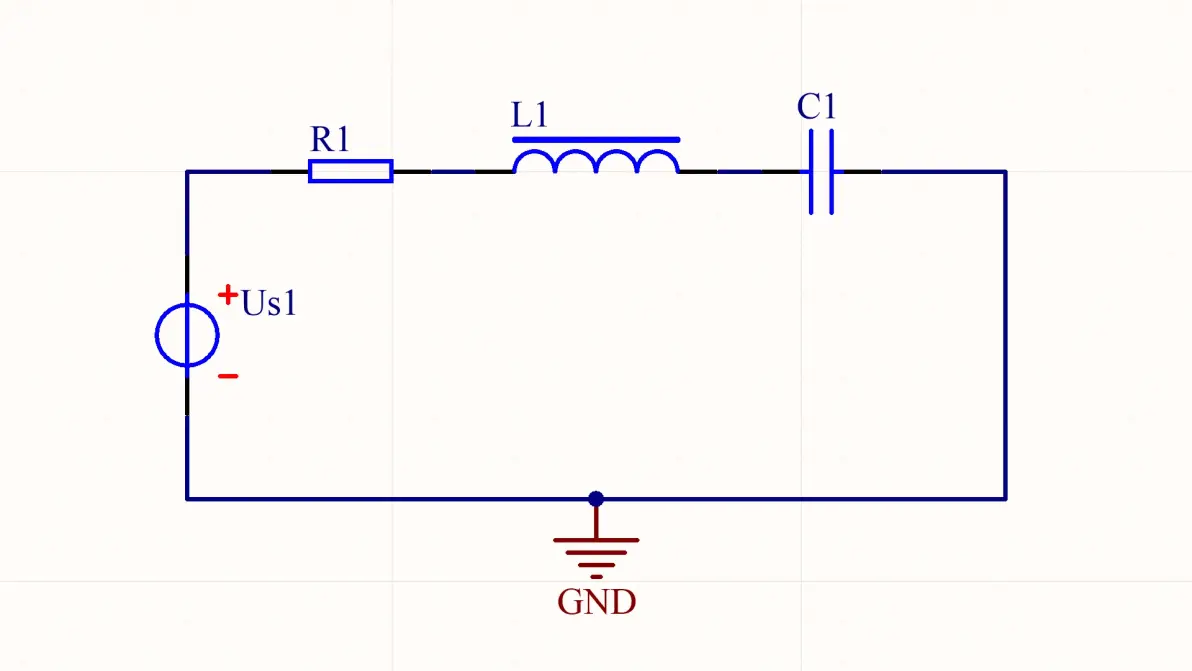
图1.1:电压源驱动的RLC串联电路
1.1 公式
为方便后续讨论,先定义以下符号,符号意义可参考以前的文章
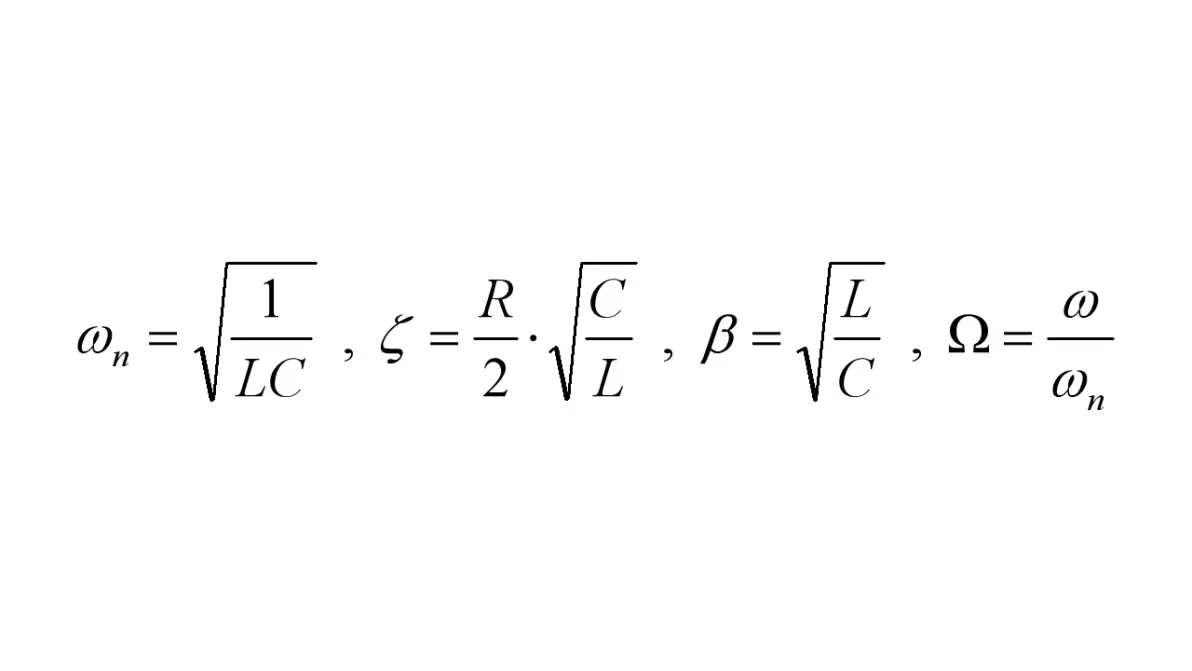
图1.2:符号定义
串联电路所有元件电流相等,因此先解算电流有效值(Irms)(元件已达到稳态)
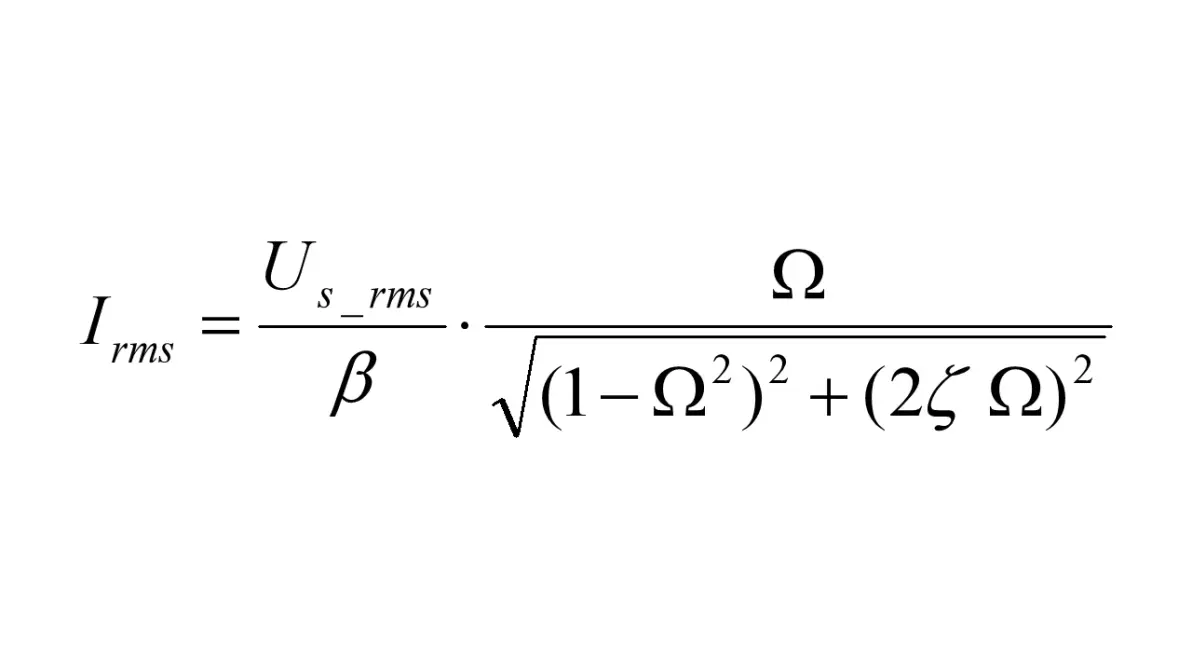
图1.3:RLC串联电路正弦电压激励元件电流
根据RLC三种元件的电压与电流的关系,可得三种元件的电压有效值(Urms)为
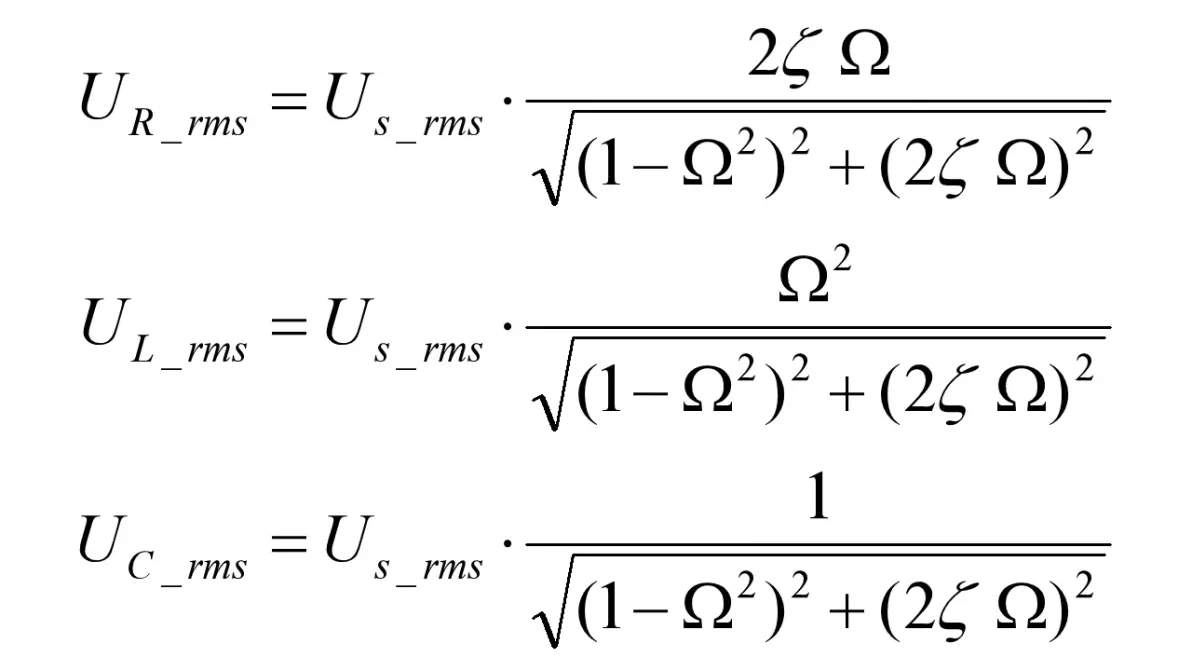
图1.4:RLC串联电路正弦电压激励元件电压
功率=电压×电流,因此RLC三种元件和激励源的视在功率(S)为
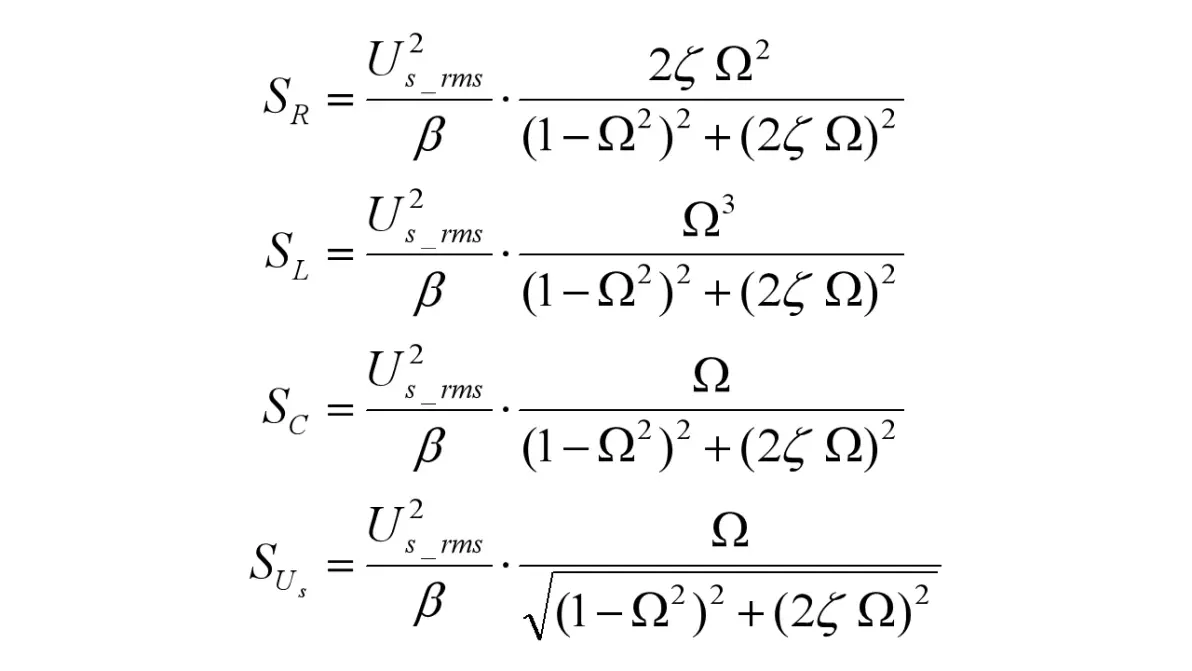
图1.5:RLC串联电路正弦电压激励元件视在功率
1.2 图像
将以上公式绘制成图像,由于ζ的不同会导致图像某些部分差异巨大,因此分别选取ζ = {0.088, 0.250, 0.500, 0.707, 1.414, 4.000}进行作图。以下为元件电流(Irms)图像
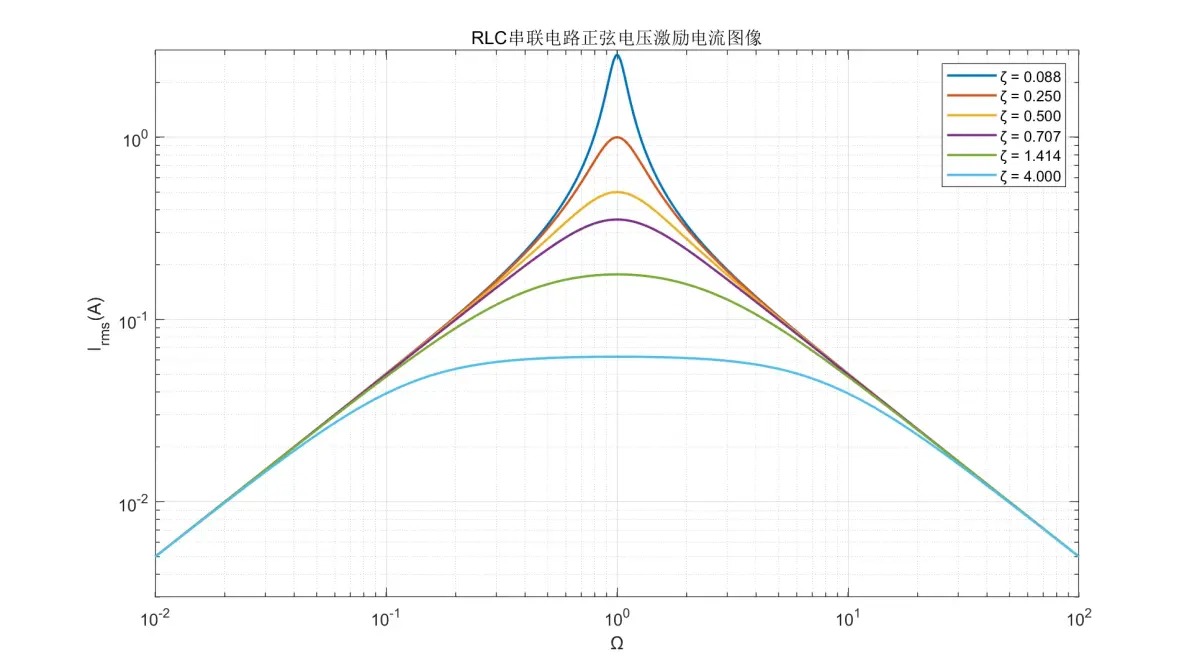
图1.6:RLC串联电路正弦电压激励元件电流图像
以下为元件电压(Urms)图像
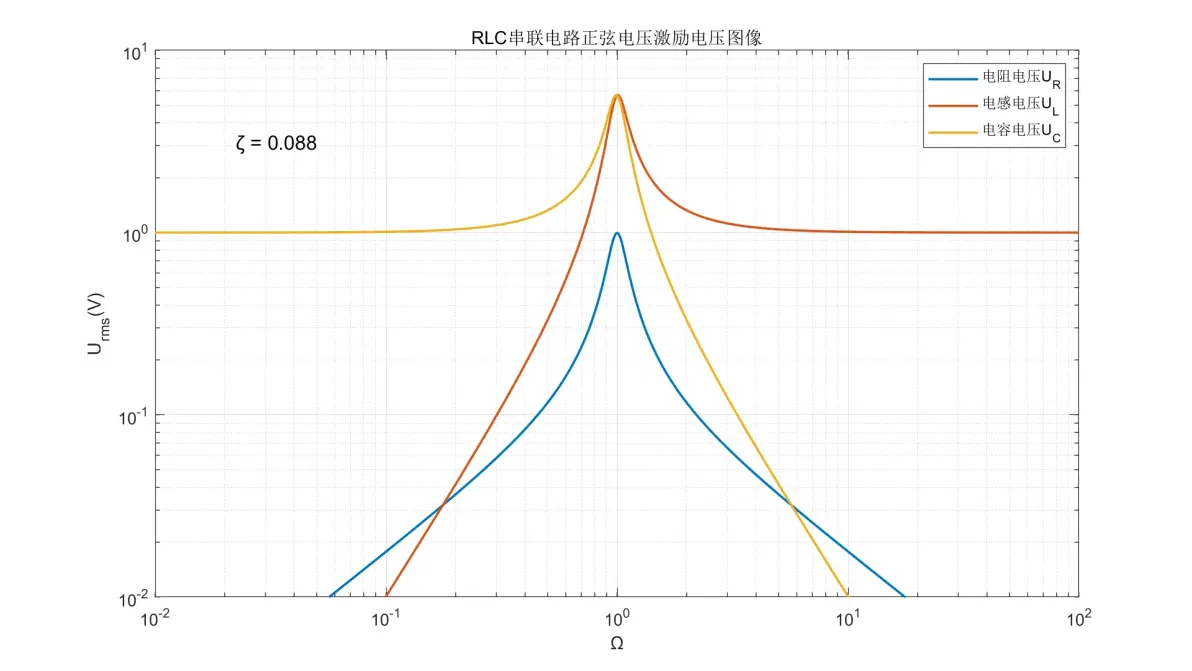
图1.7:RLC串联电路正弦电压激励元件电压图像(ζ = 0.088)
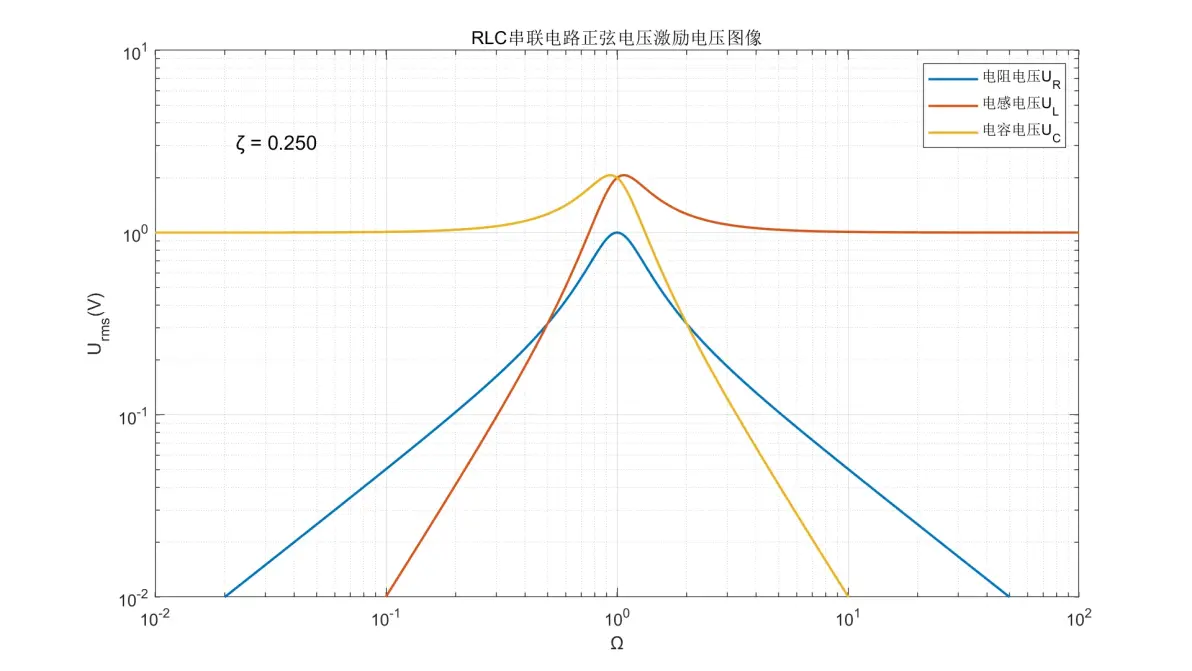
图1.8:RLC串联电路正弦电压激励元件电压图像(ζ = 0.250)
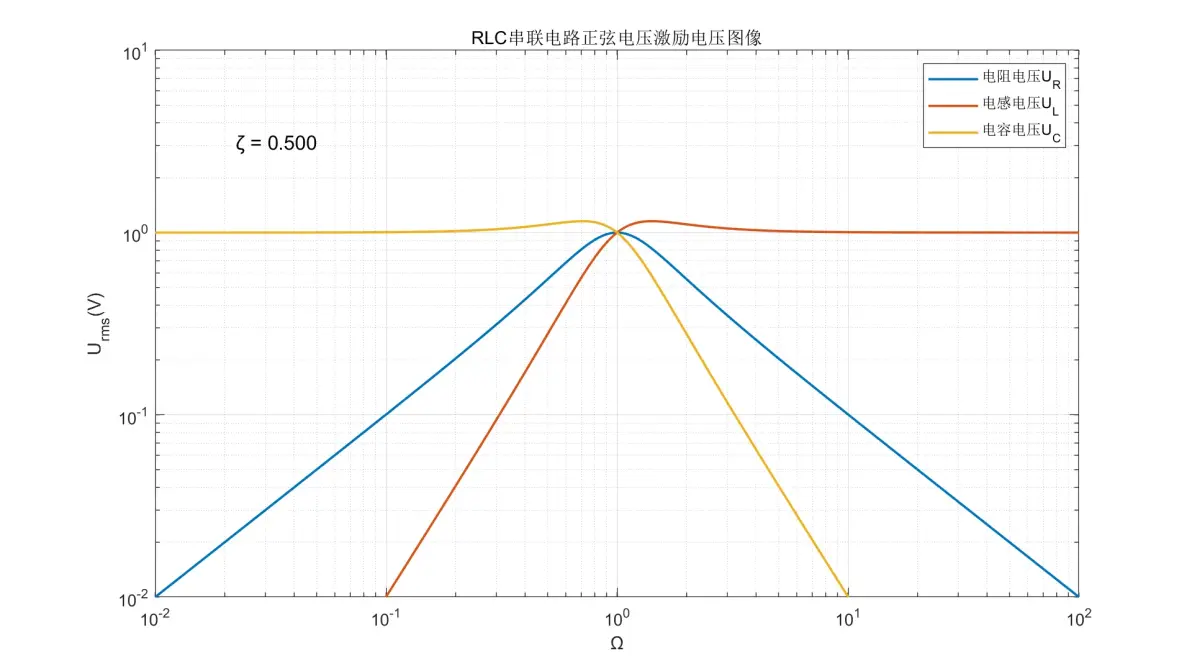
图1.9:RLC串联电路正弦电压激励元件电压图像(ζ = 0.500)
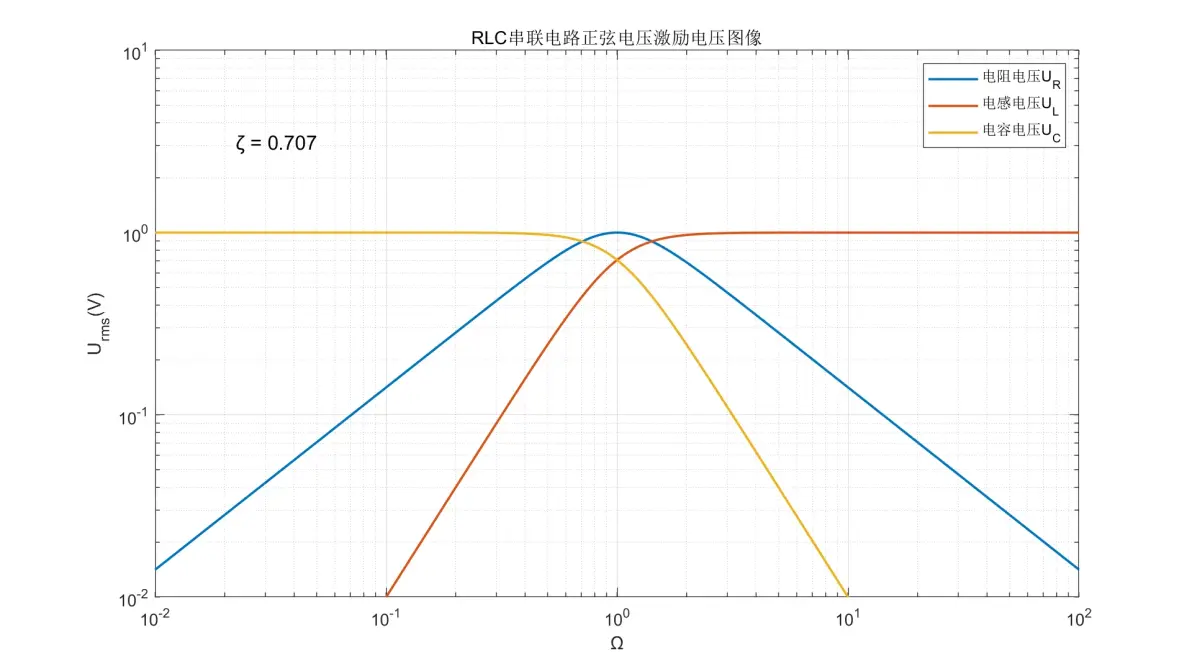
图1.10:RLC串联电路正弦电压激励元件电压图像(ζ = 0.707)
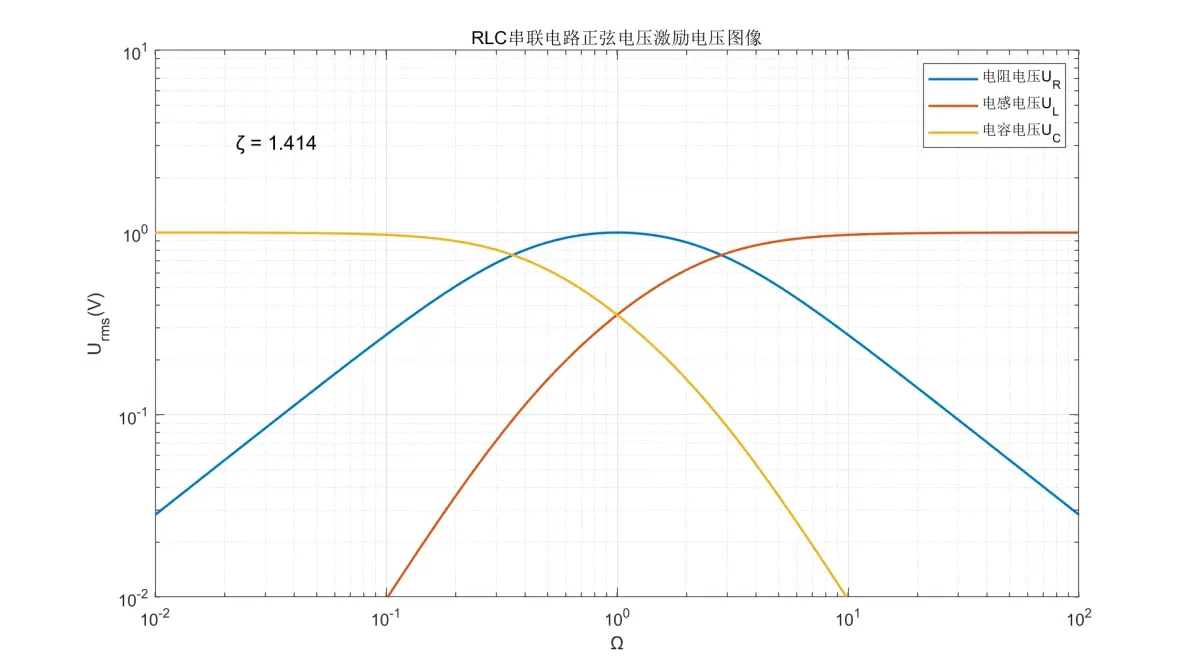
图1.11:RLC串联电路正弦电压激励元件电压图像(ζ = 1.414)
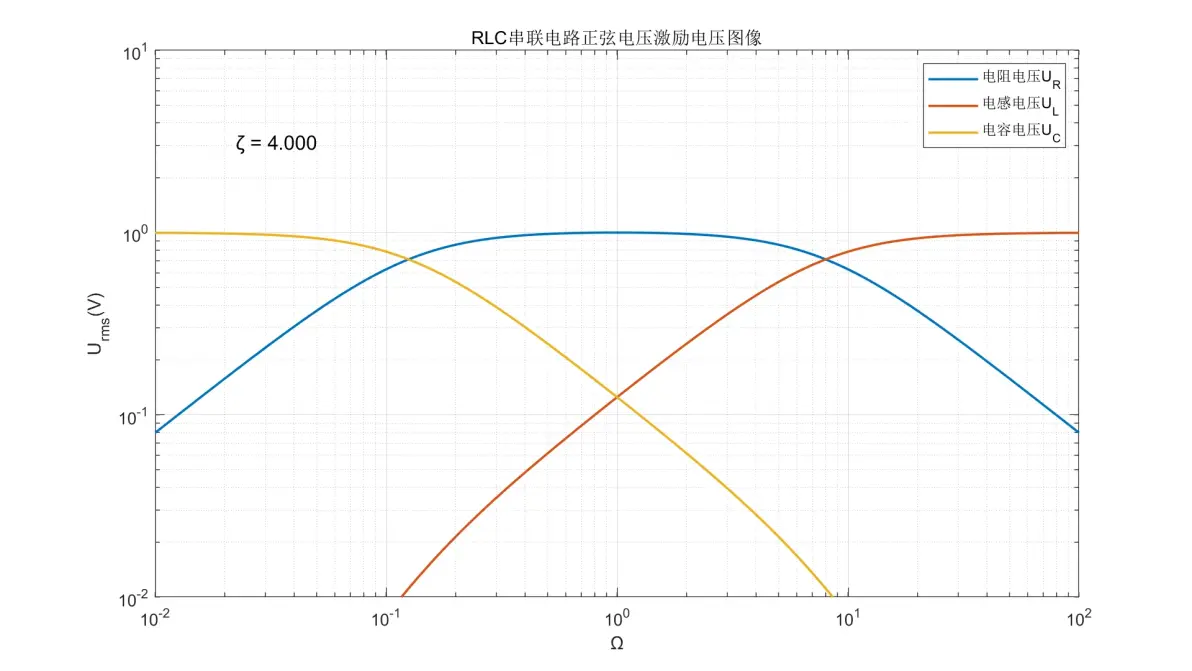
图1.12:RLC串联电路正弦电压激励元件电压图像(ζ = 4.000)
以下为元件功率(S)图像
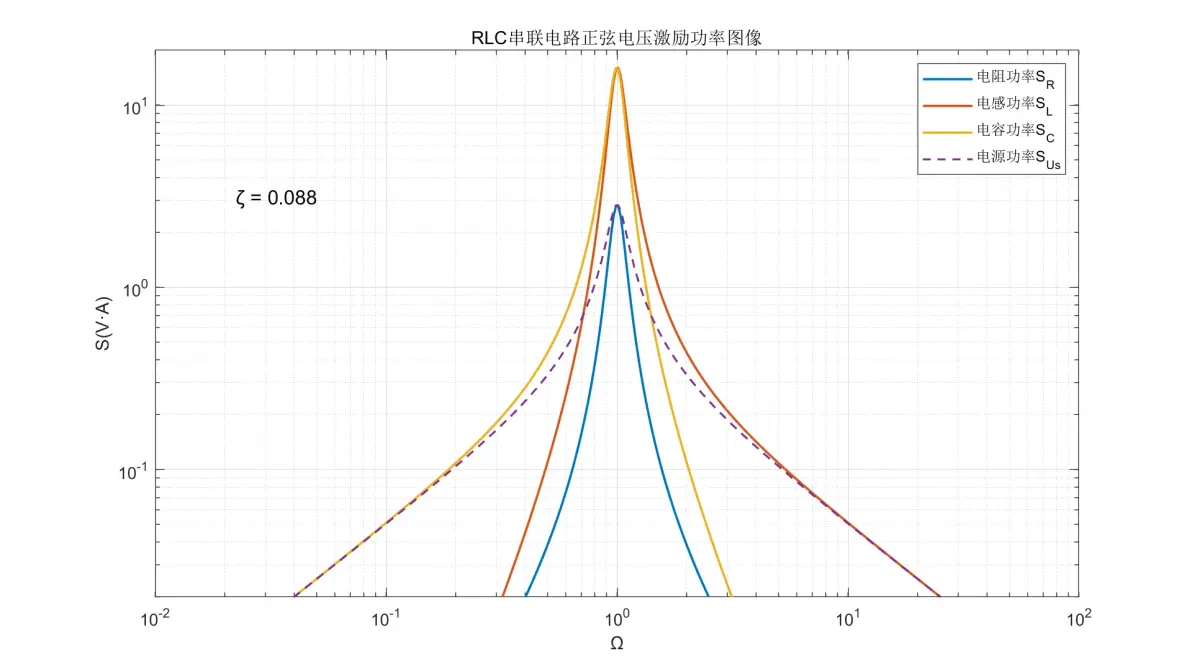
图1.13:RLC串联电路正弦电压激励元件功率图像(ζ = 0.088)
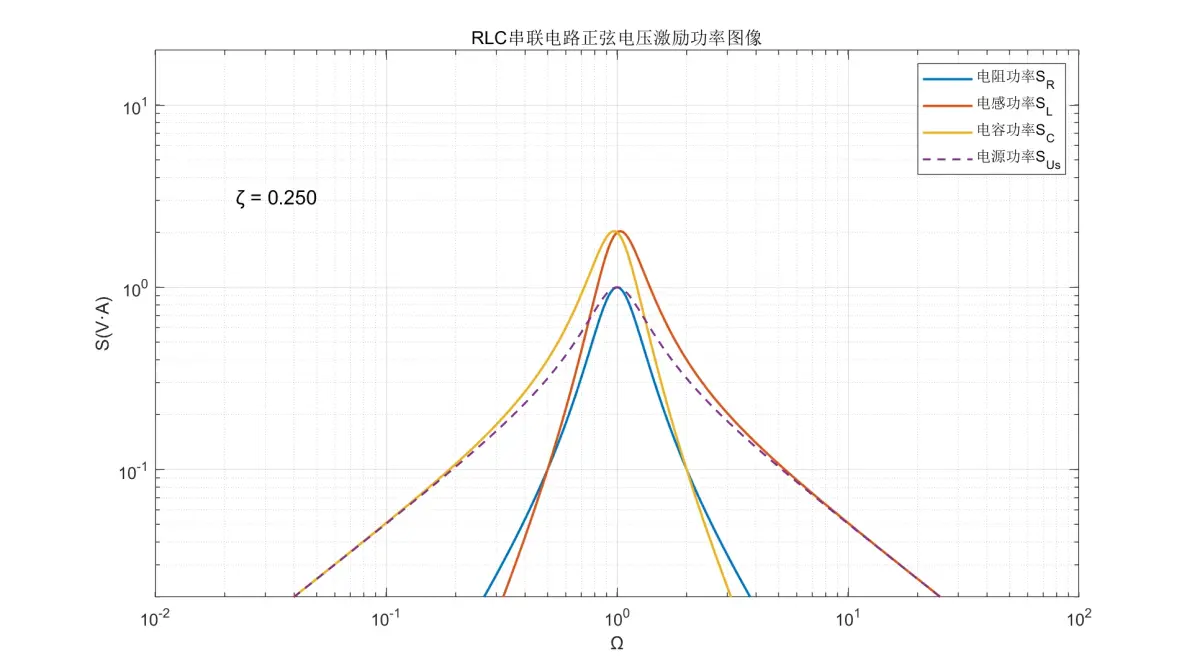
图1.14:RLC串联电路正弦电压激励元件功率图像(ζ = 0.250)
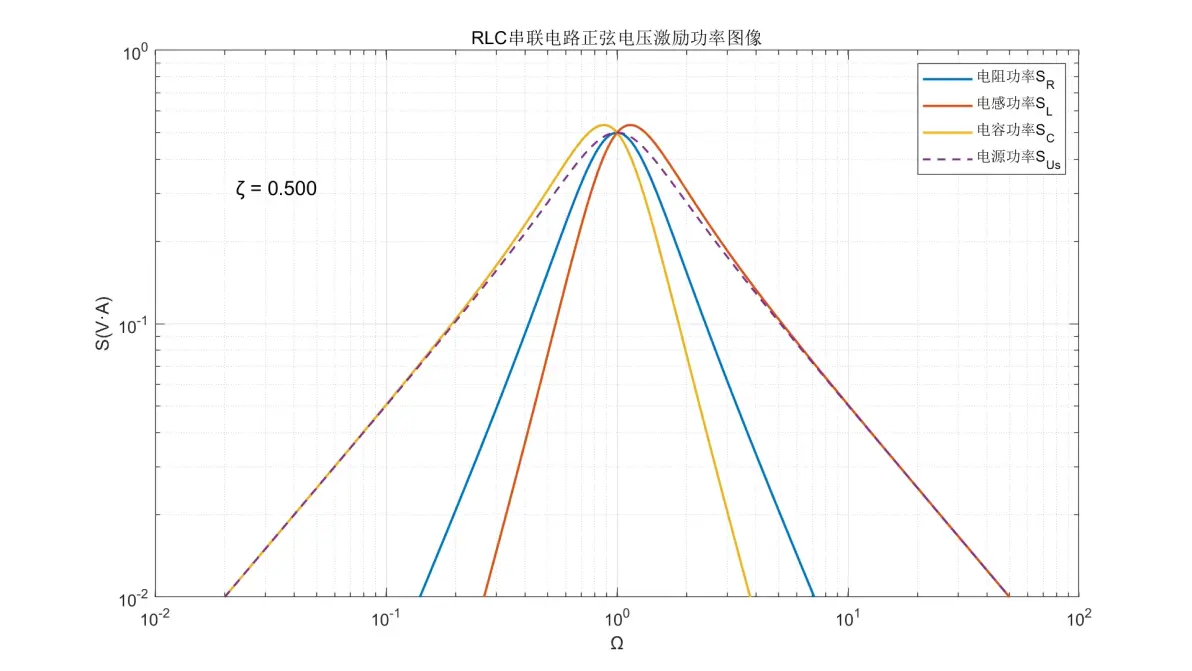
图1.15:RLC串联电路正弦电压激励元件功率图像(ζ = 0.500)

图1.16:RLC串联电路正弦电压激励元件功率图像(ζ = 0.707)
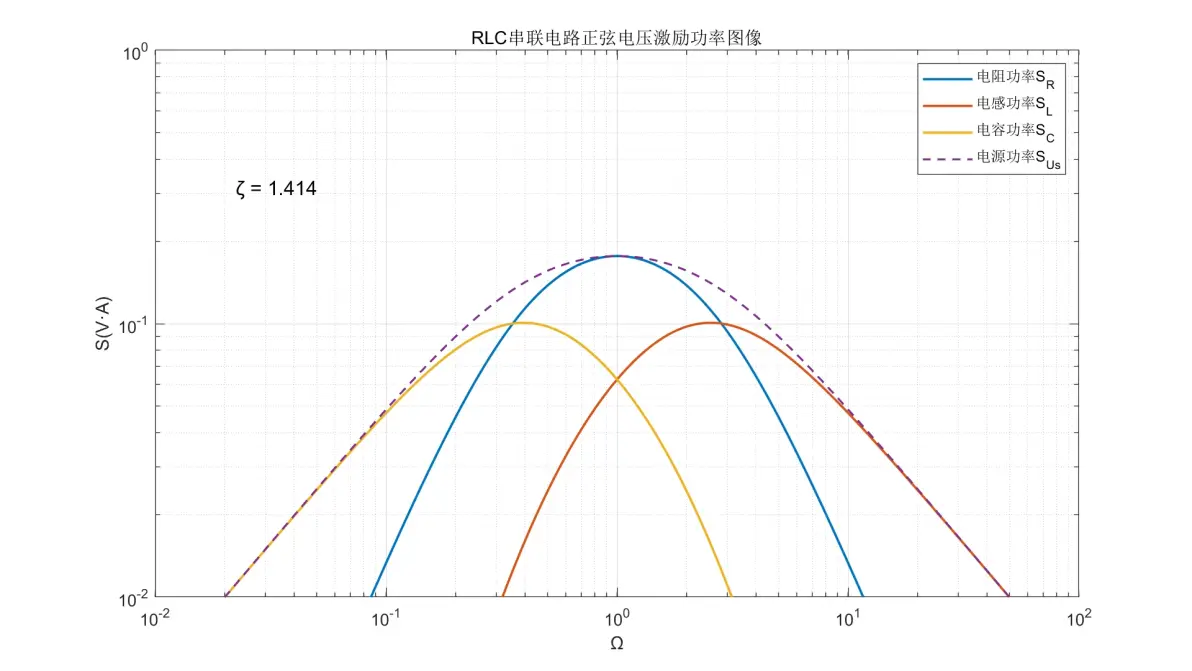
图1.17:RLC串联电路正弦电压激励元件功率图像(ζ = 1.414)
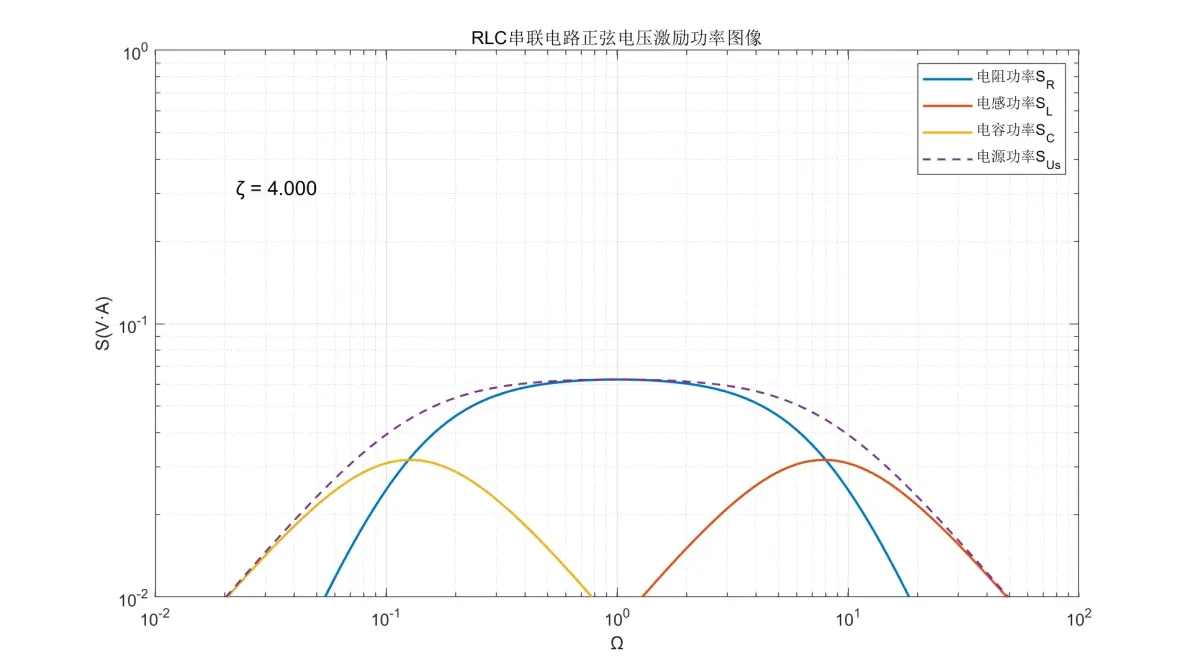
图1.18:RLC串联电路正弦电压激励元件功率图像(ζ = 4.000)
1.3 规律总结
(1) 电阻、电感、电容三个元件的电流变化规律一致。在Ω < 1时电流以+20dB/dec的速率增加;并在Ω = 1时达到最大值;Ω > 1时则以-20dB/dec的速率减弱。
(2) 电阻的电压变化规律与电流一致。
(3) 电感的电压变化规律会在电流基础上+20dB。Ω < 1时,电压以+40dB/dec增加;Ω > 1则变成±0dB/dec保持稳定;Ω = 1附近会随ζ的不同有不同行为。
(4) 电容的电压变化规律会在电流基础上-20dB。Ω < 1时,电压保持±0dB/dec;Ω > 1则以-40dB/dec减少;Ω = 1附近会随ζ的不同有不同行为。
(5) 电阻的功率在Ω < 1时以+40dB/dec增加;Ω > 1时以-40dB/dec减弱;Ω = 1时达到最大。
(6) 电感的功率在Ω < 1时以+60dB/dec增加;Ω > 1时以-20dB/dec减弱;Ω = 1时取决于ζ。
(7) 电容的功率在Ω < 1时以+20dB/dec增加;Ω > 1时以-60dB/dec减弱;Ω = 1时取决于ζ。
(8) 电源的功率在Ω < 1时以+20dB/dec增加;Ω > 1时以-20dB/dec减弱;Ω = 1时达到最大。
(9) 电源的电压和功率在Ω < 1时几乎由电容全部承受,此时Us = UC >> UR >> UL,Ss = SC >> SR >> SL;Ω = 1时由电阻全部承受;Ω > 1时几乎由电感全部承受,此时Us = UL >> UR >> UC,Ss = SL >> SR >> SC。
(10) ζ的值会大幅影响Ω = 1附近各元件的行为。当ζ ≥ 0.707时系统不会发生谐振,此时UL和UC均≤ Us,SL和SC均≤ Ss;当ζ < 0.5时,系统谐振强度变高,全频率内UL和UC均> UR并且≥Us,SL和SC均> SR并且≥ Ss。
将以上部分规律总结为表格

图1.19:RLC串联电路正弦电压激励部分规律
2、正弦电压源驱动的RLC并联电路
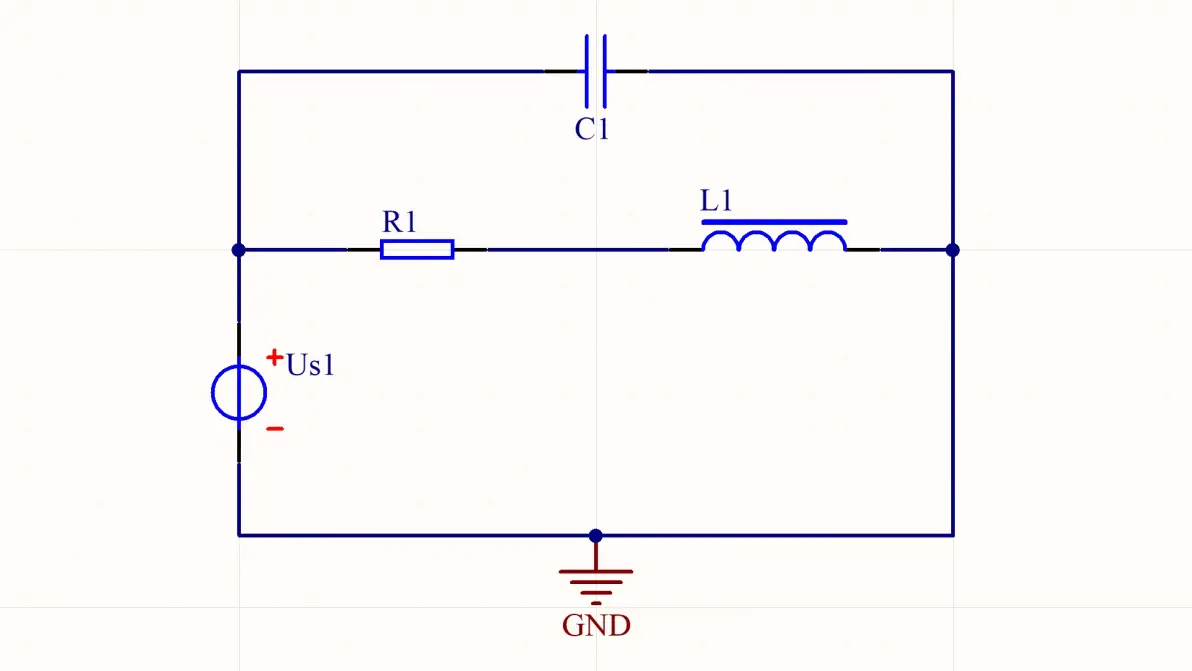
图2.1:电压源驱动的RLC并联电路
2.1 公式
符号定义同前章
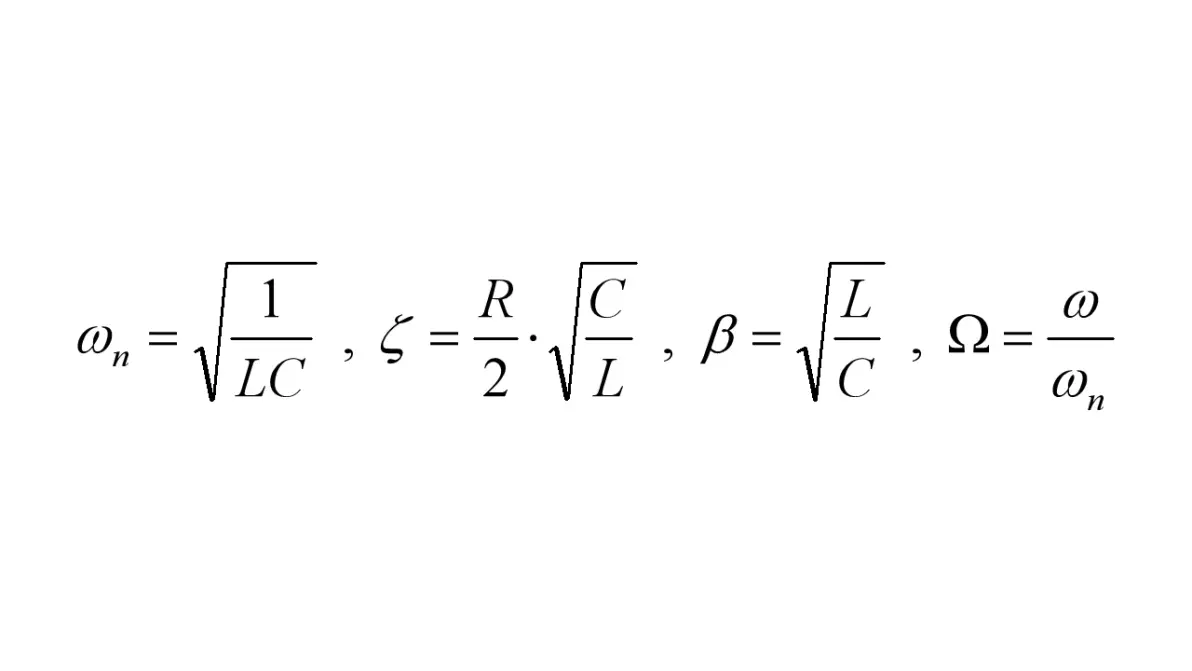
图2.2:符号定义
该电路拥有两个节点和两个支路,共拥有三个拓扑约束:uS = uC = uR+uL,iR = iL,ius = iL+iC,经计算得各元件电流有效值(Irms)(元件已达到稳态)
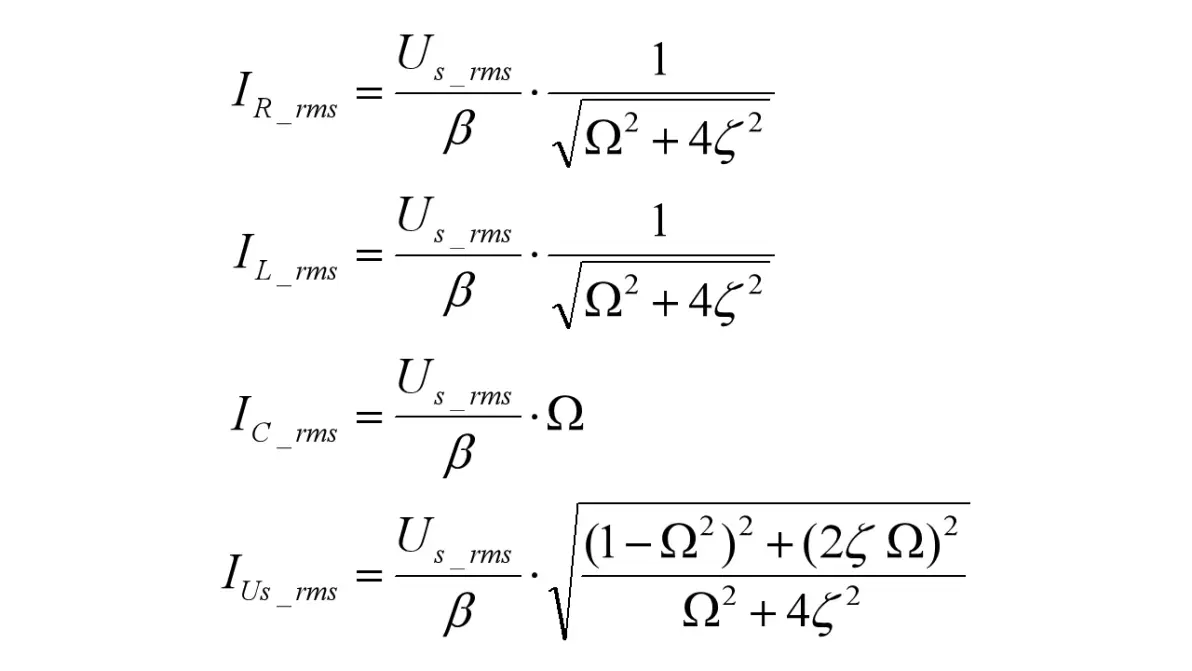
图2.3:RLC并联电路正弦电压激励元件电流
三种元件的电压有效值(Urms)为
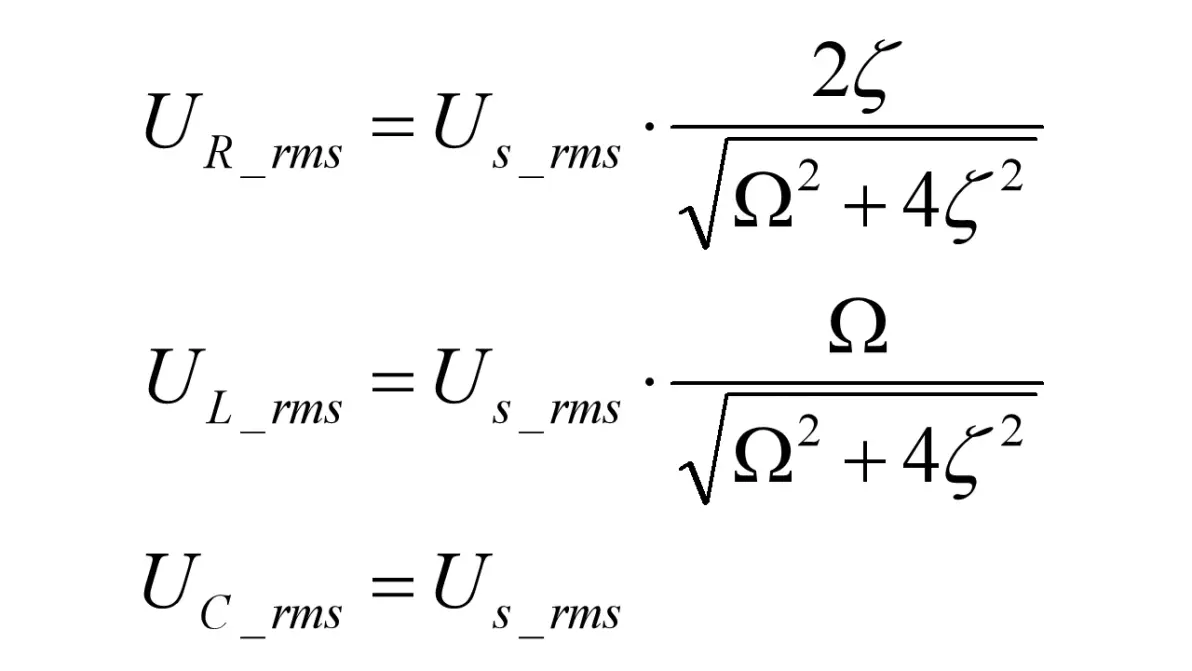
图2.4:RLC并联电路正弦电压激励元件电压
最终RLC三种元件和激励源的视在功率(S)为

图2.5:RLC并联电路正弦电压激励元件视在功率
2.2 图像
将以上公式绘制成图像,由于ζ的不同会导致图像某些部分差异巨大,因此分别选取ζ = {0.088, 0.250, 0.500, 0.707, 1.414, 4.000}进行作图。以下为元件电流(Irms)图像
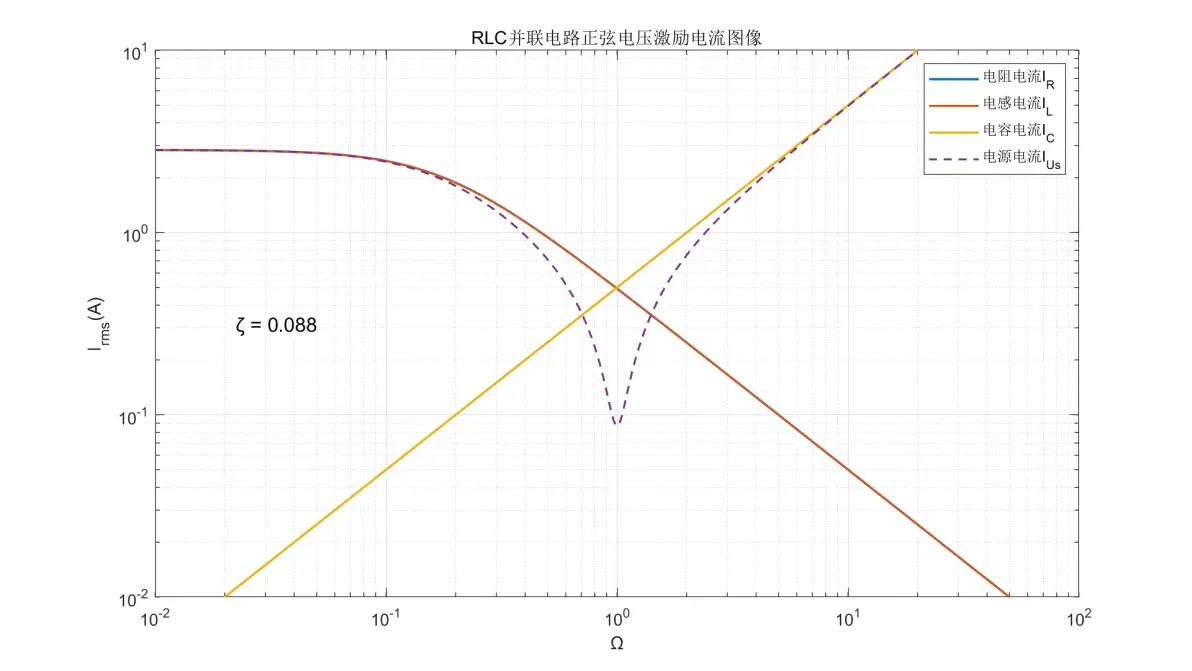
图2.6:RLC并联电路正弦电压激励元件电流图像(ζ = 0.088)
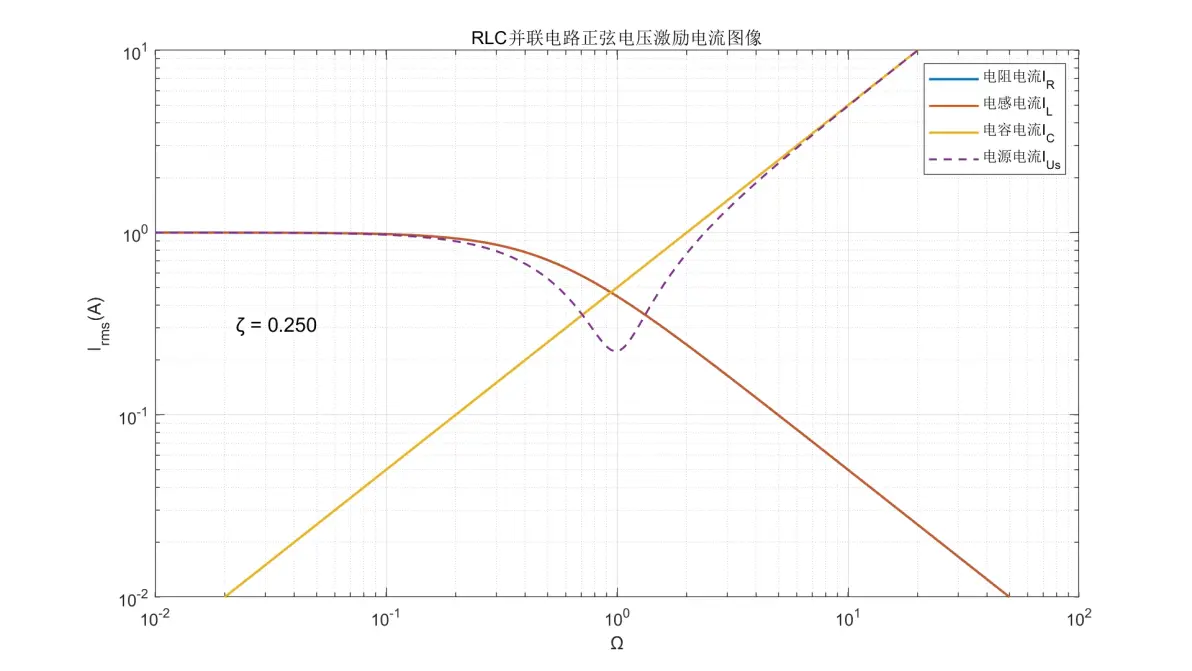
图2.7:RLC并联电路正弦电压激励元件电流图像(ζ = 0.250)
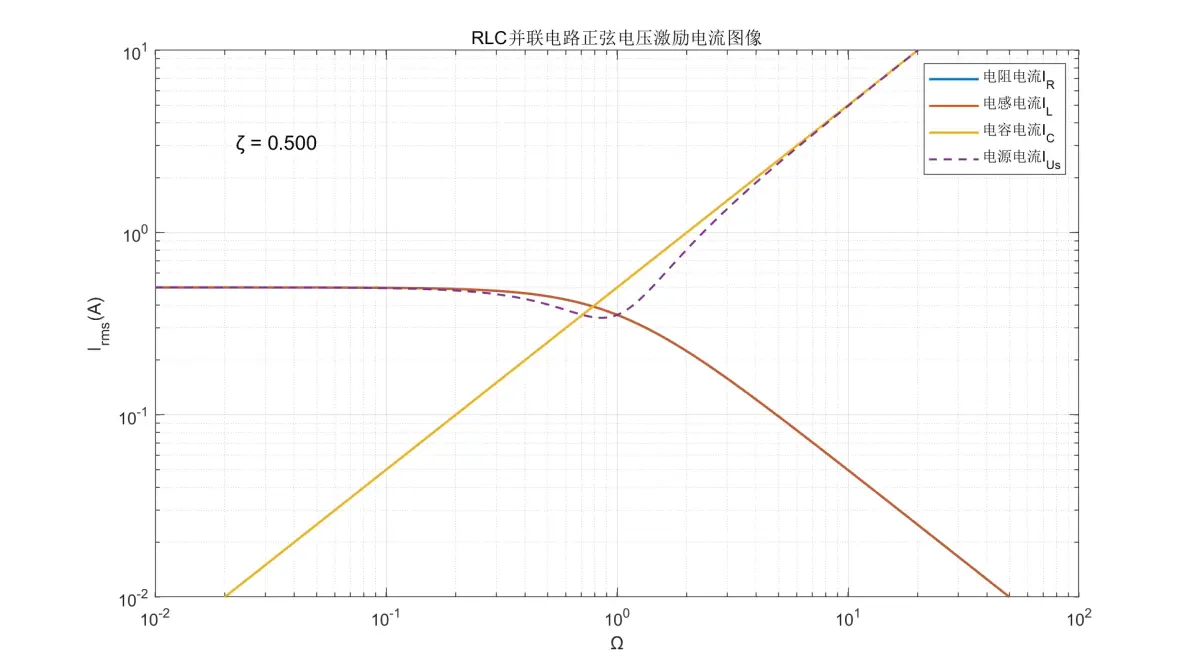
图2.8:RLC并联电路正弦电压激励元件电流图像(ζ = 0.500)

图2.9:RLC并联电路正弦电压激励元件电流图像(ζ = 0.707)

图2.10:RLC并联电路正弦电压激励元件电流图像(ζ = 1.414)
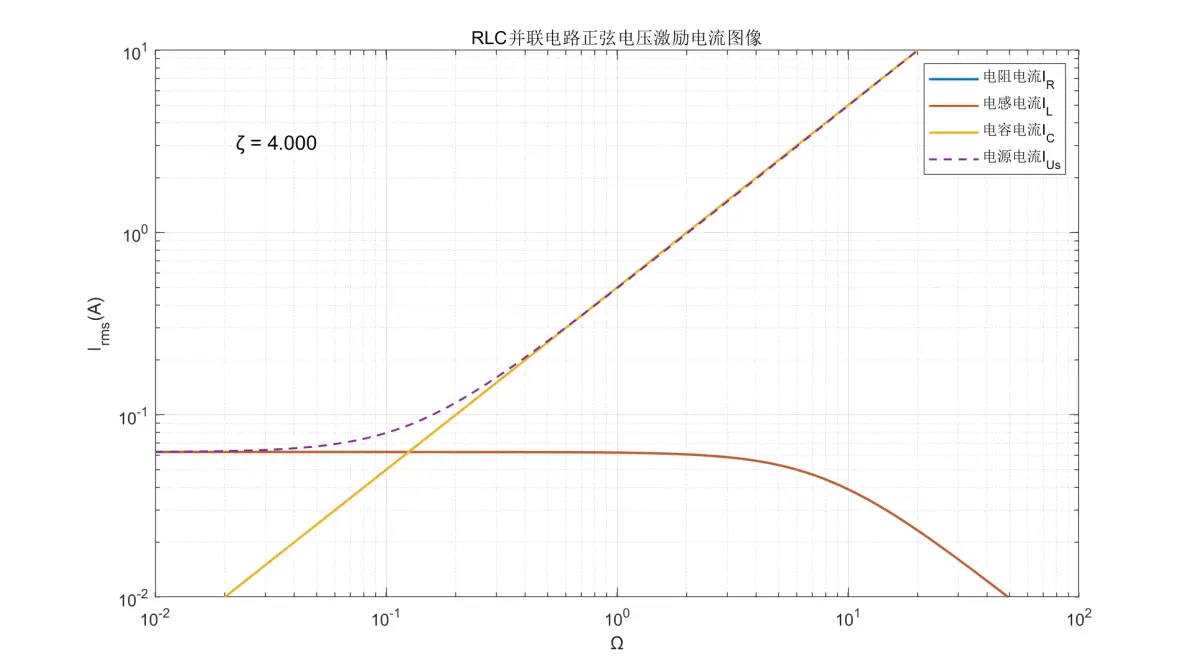
图2.11:RLC并联电路正弦电压激励元件电流图像(ζ = 4.000)
以下为元件电压(Urms)图像
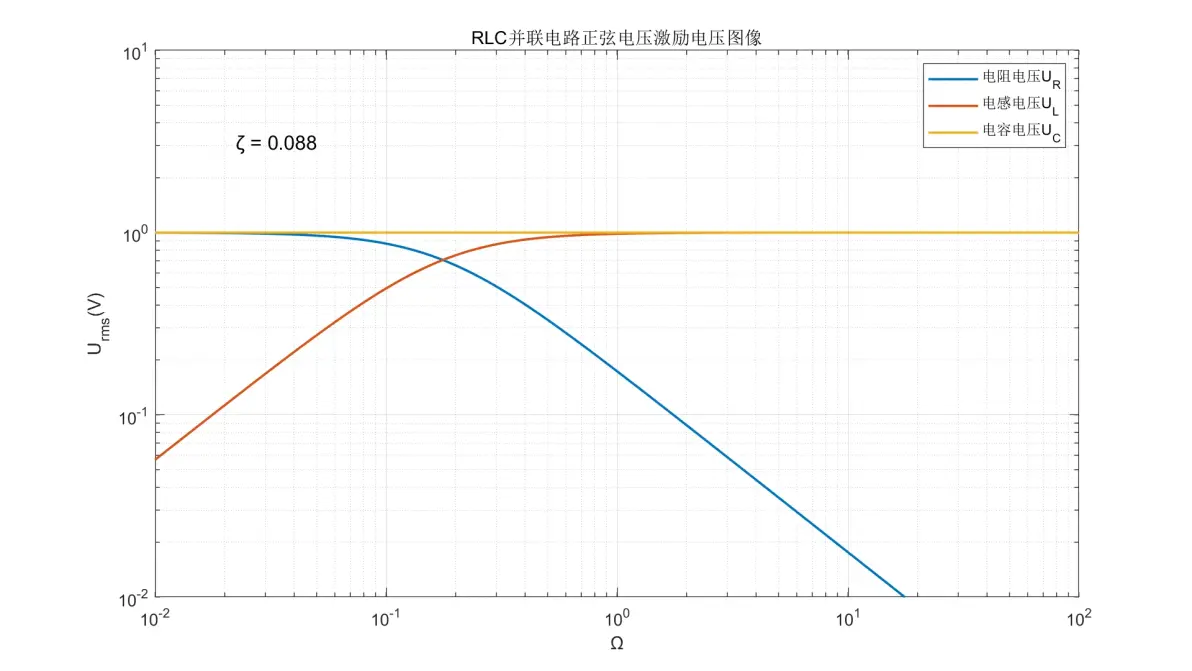
图2.12:RLC并联电路正弦电压激励元件电压图像(ζ = 0.088)
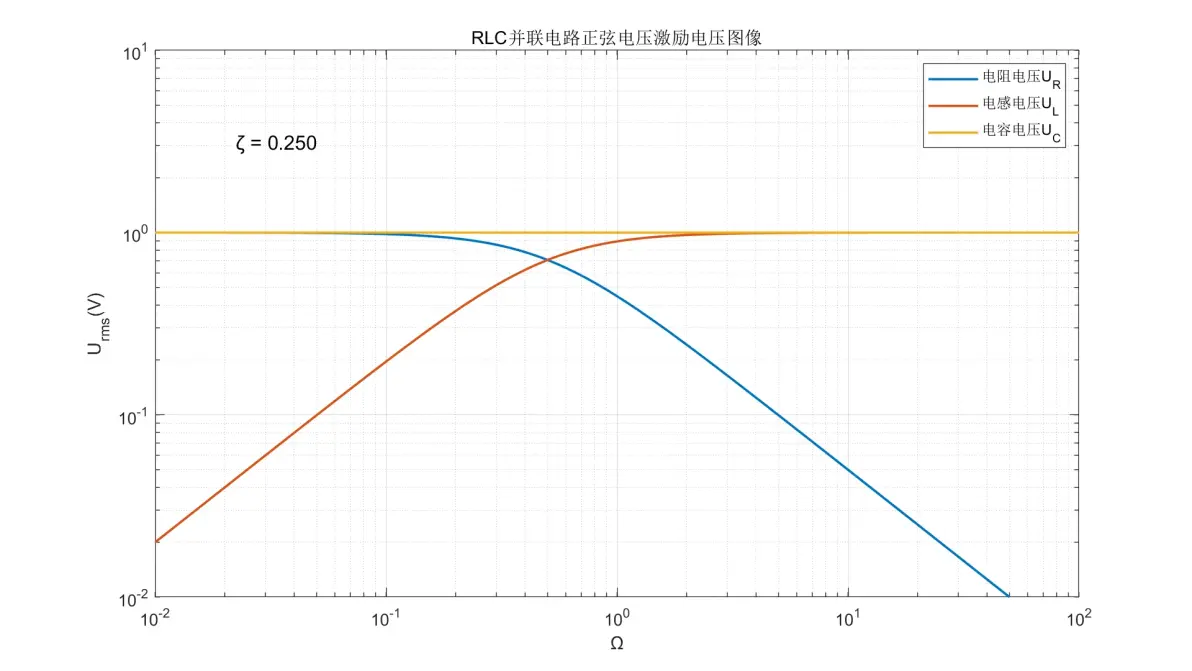
图2.13:RLC并联电路正弦电压激励元件电压图像(ζ = 0.250)
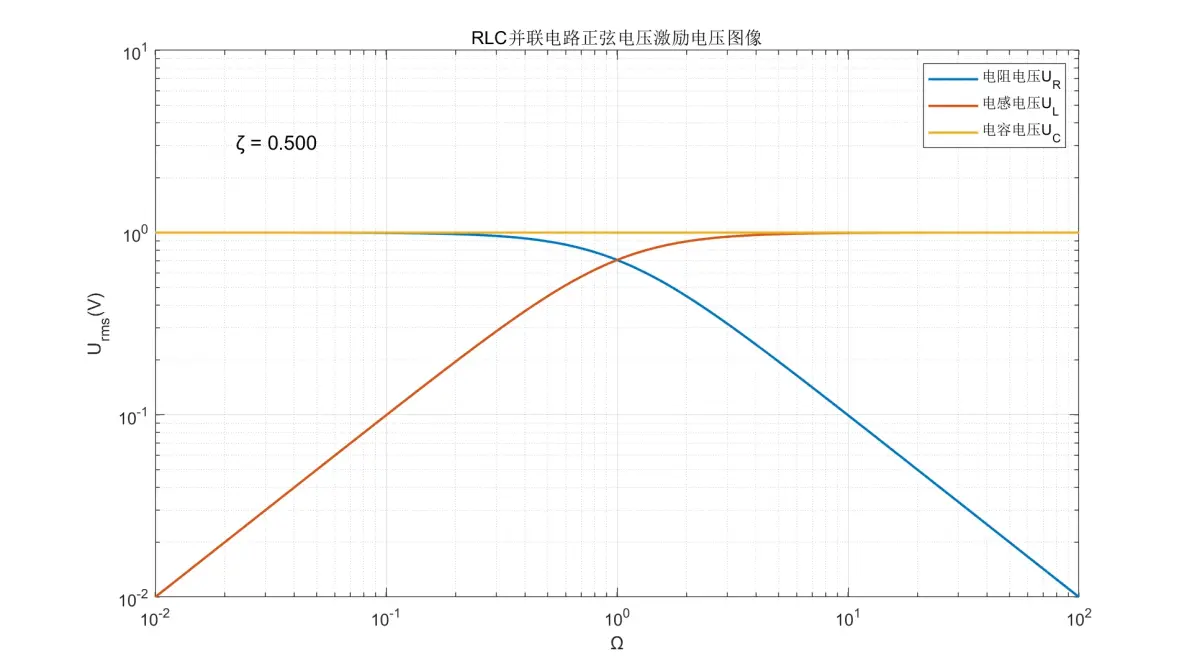
图2.14:RLC并联电路正弦电压激励元件电压图像(ζ = 0.500)
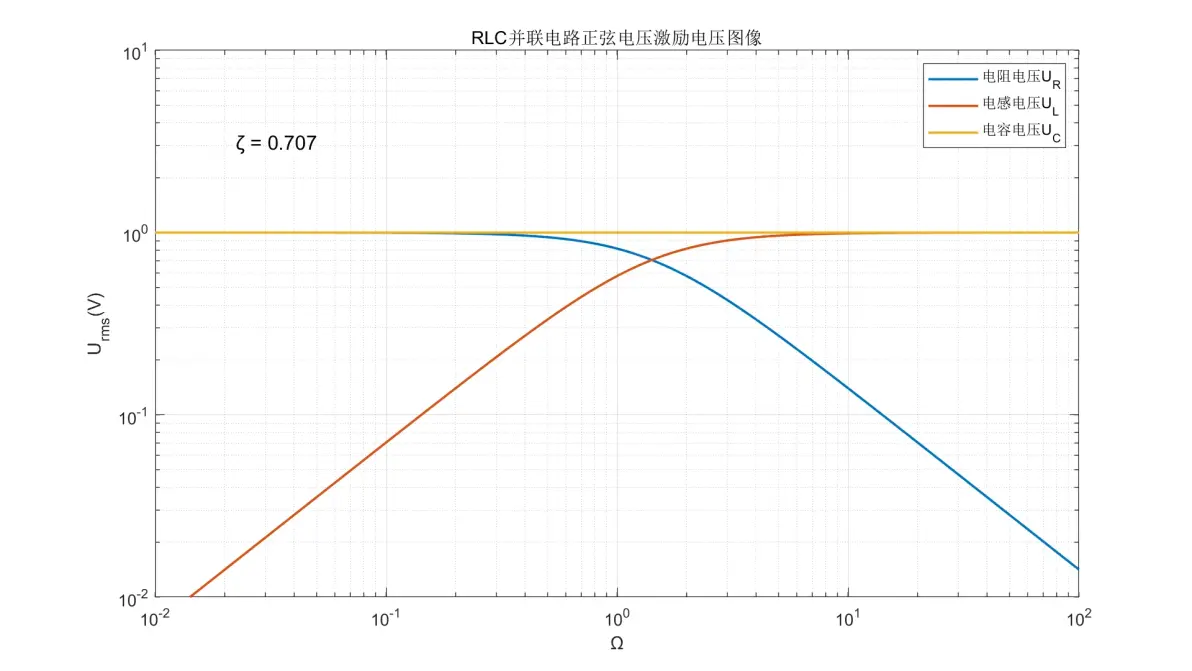
图2.15:RLC并联电路正弦电压激励元件电压图像(ζ = 0.707)
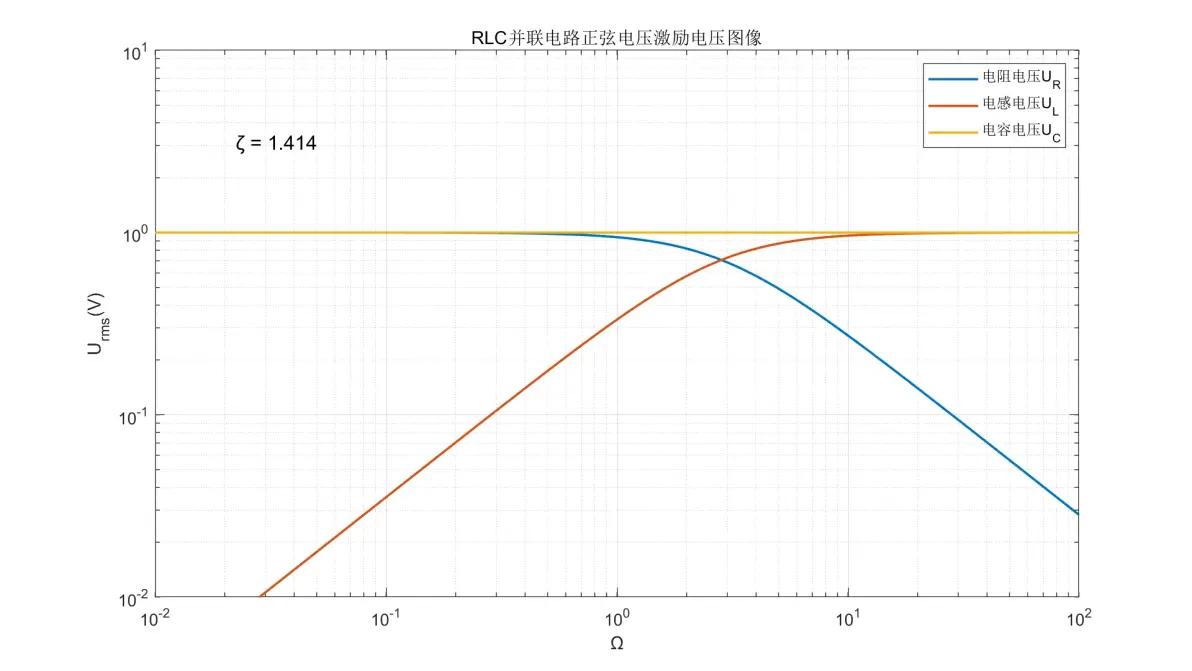
图2.16:RLC并联电路正弦电压激励元件电压图像(ζ = 1.414)
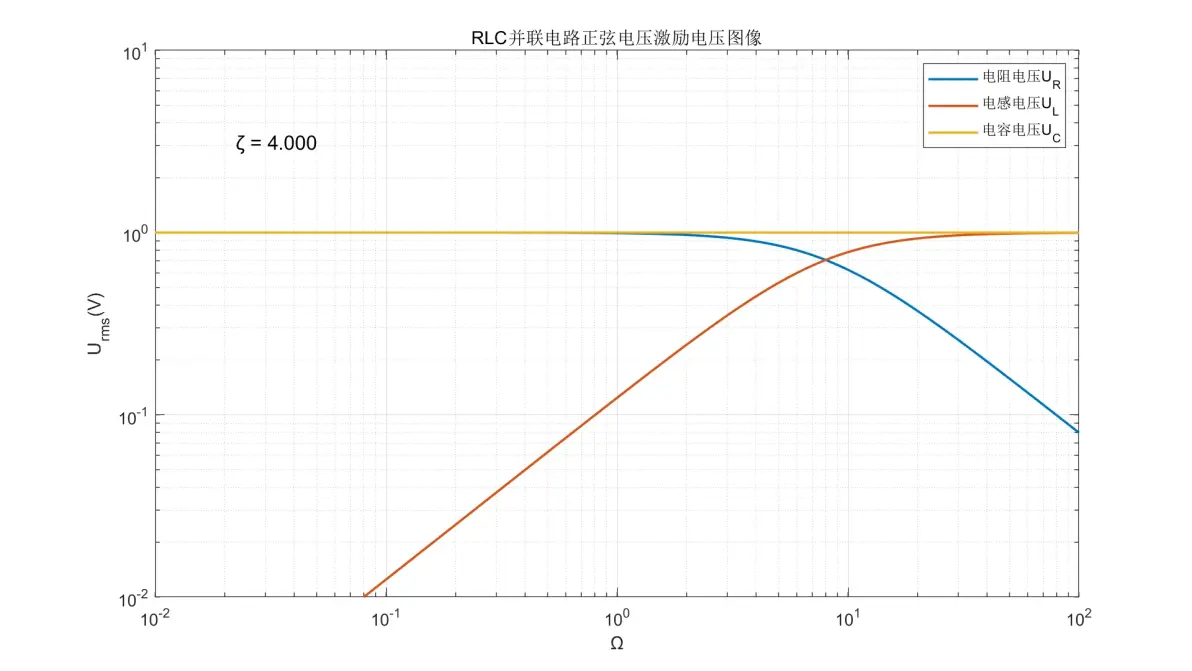
图2.17:RLC并联电路正弦电压激励元件电压图像(ζ = 4.000)
以下为元件功率(S)图像
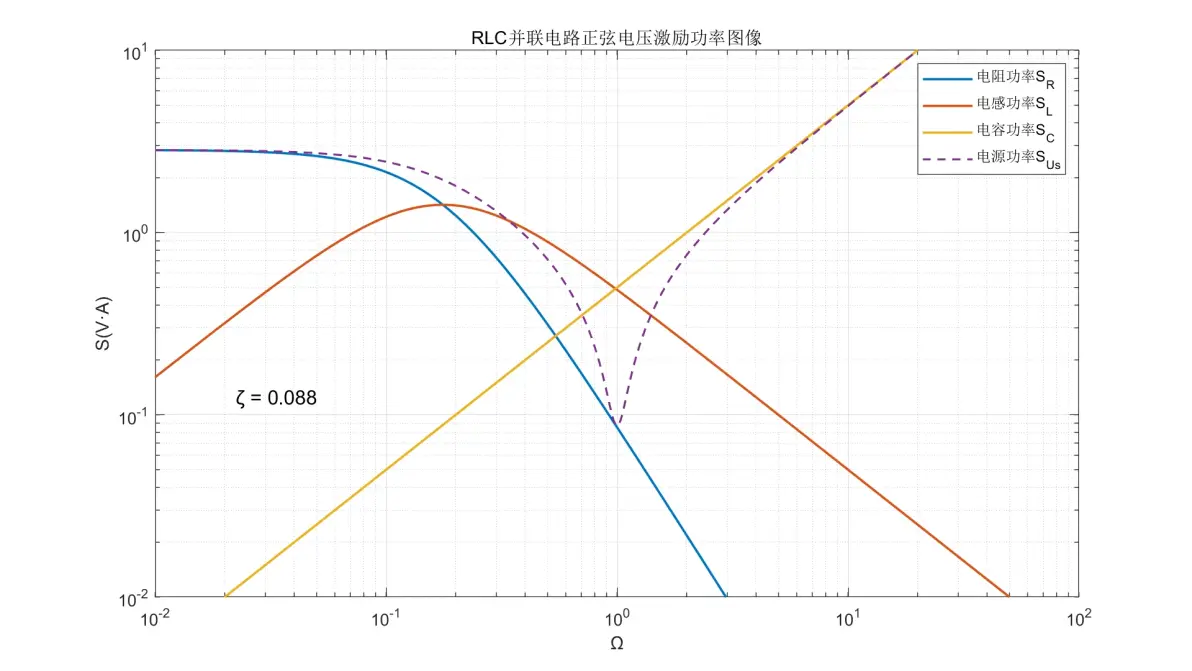
图2.18:RLC并联电路正弦电压激励元件功率图像(ζ = 0.088)
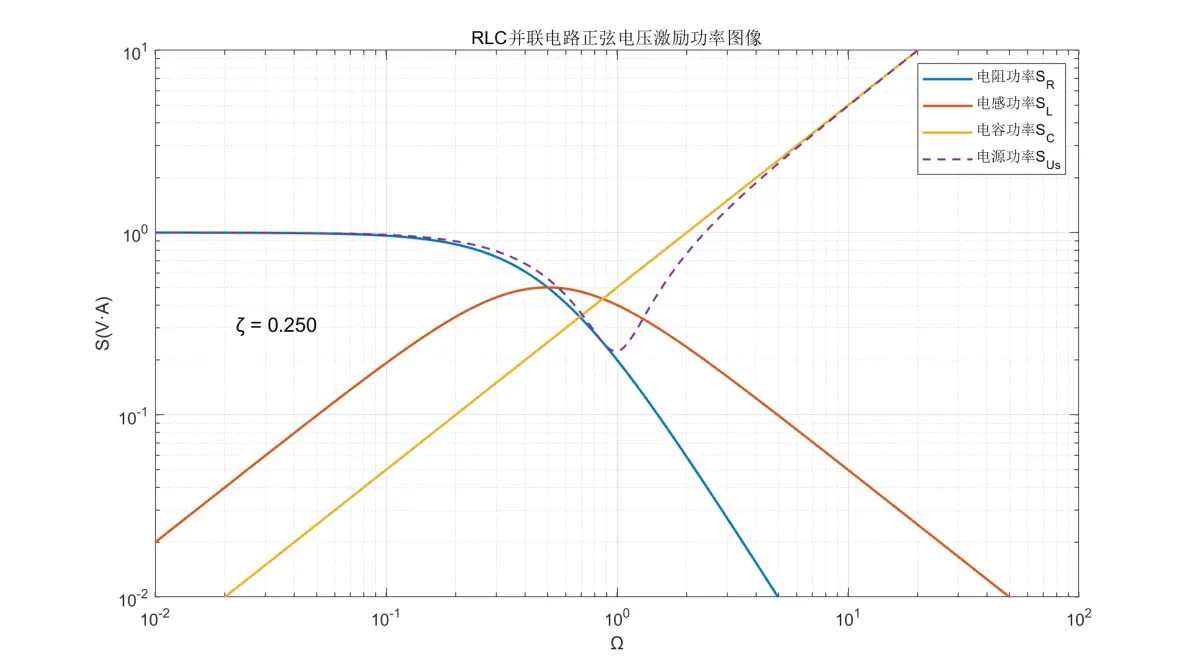
图2.19:RLC并联电路正弦电压激励元件功率图像(ζ = 0.250)
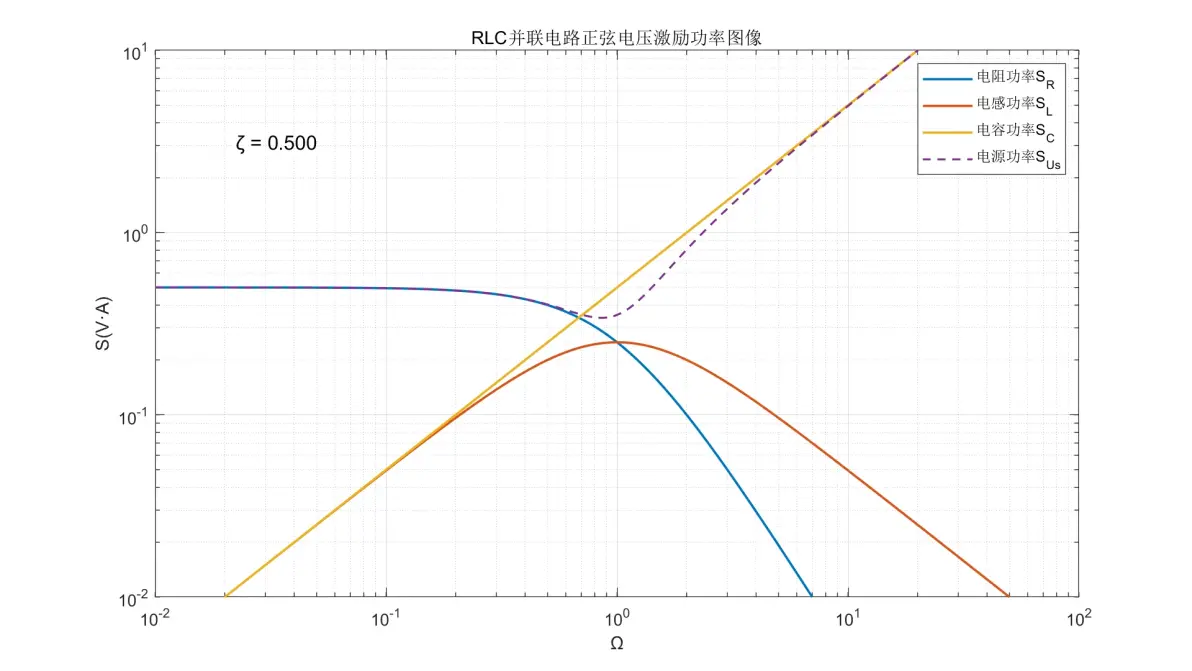
图2.20:RLC并联电路正弦电压激励元件功率图像(ζ = 0.500)
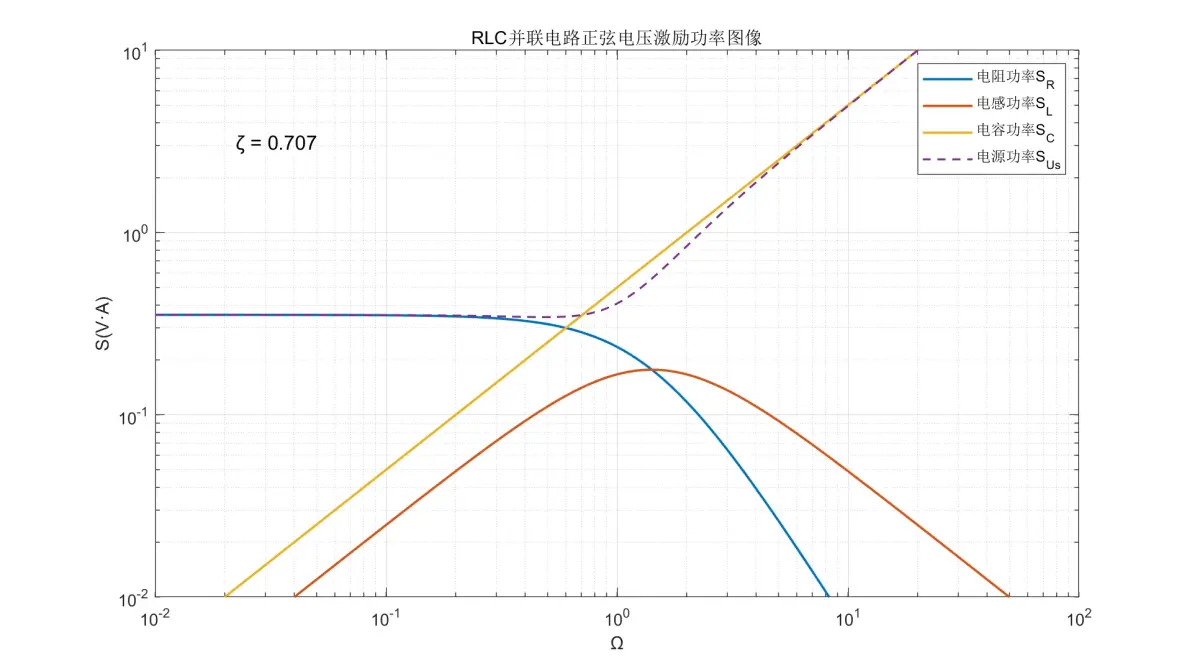
图2.21:RLC并联电路正弦电压激励元件功率图像(ζ = 0.707)
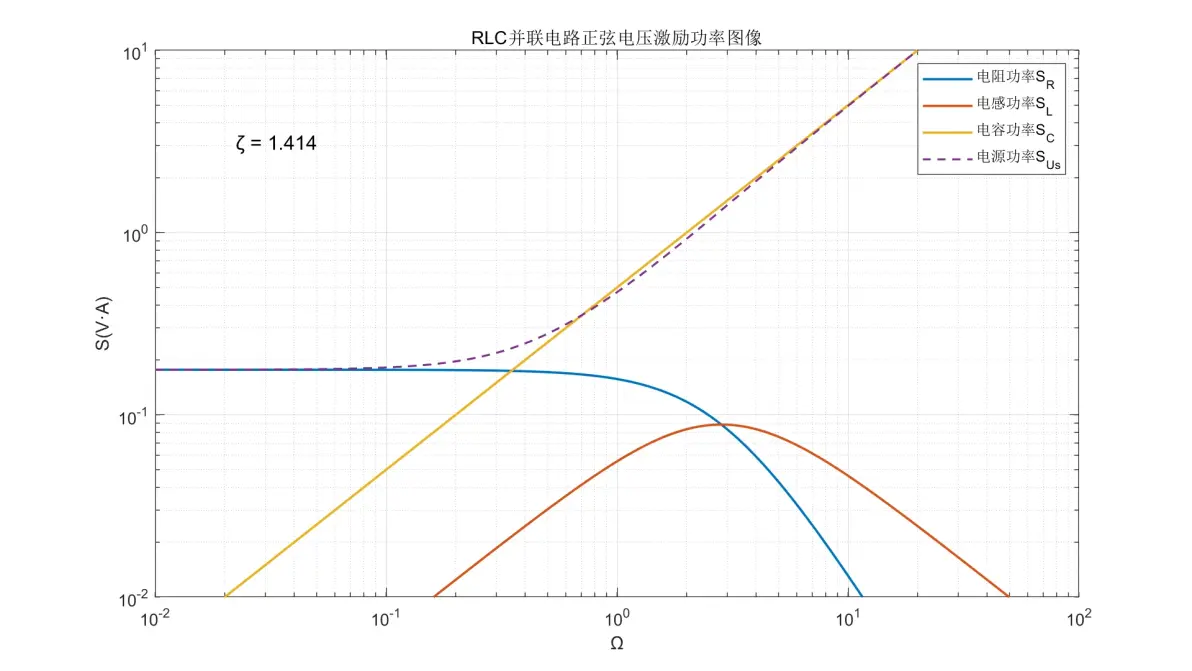
图2.22:RLC并联电路正弦电压激励元件功率图像(ζ = 1.414)
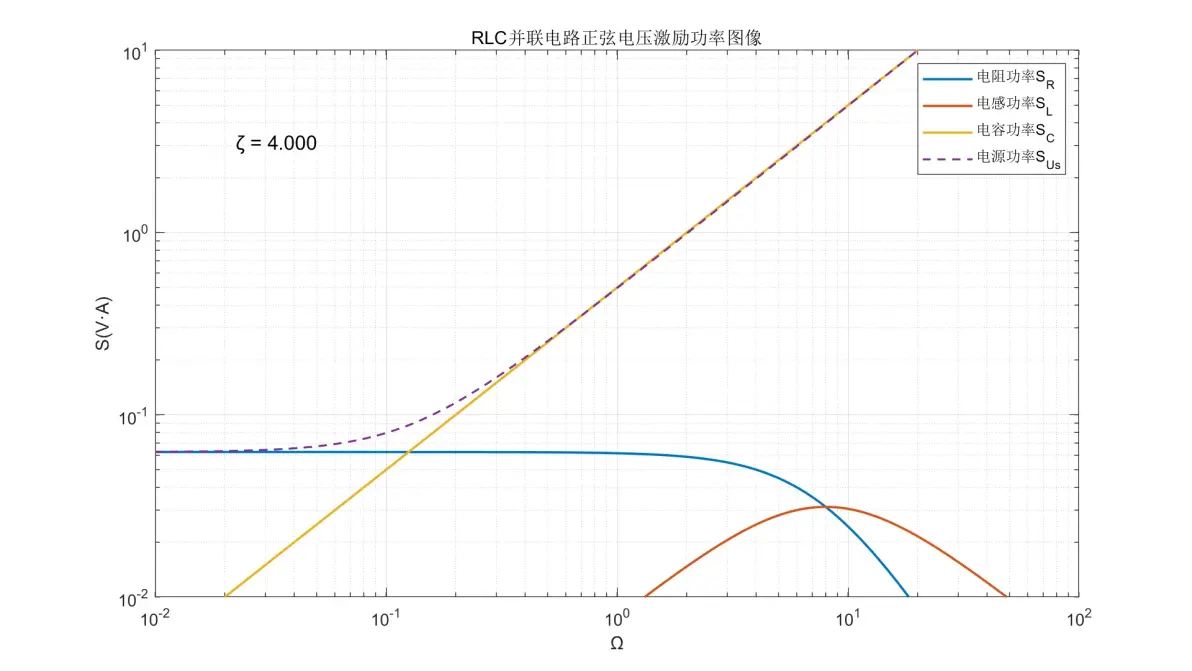
图2.23:RLC并联电路正弦电压激励元件功率图像(ζ = 4.000)
2.3 规律总结
(1) 电阻和电感的电流是同一个,其转折频率与R/L值有关。在Ω < 2ζ时电流为±0dB/dec;Ω > 2ζ时则以-20dB/dec的速率减弱。
(2) 电容的电流在全频率内均为+20dB/dec。
(3) 电源的电流为IR和IL与IC两者中的最大值;但在Ω = 1且ζ < 0.5时,电流会同时低于三者。
(4) 电阻的电压变化规律与IR一致。
(5) 电感的电压变化规律与UR正好相反。
(6) 电容的电压在全频率内均等于Us。
(7) 电阻的功率在Ω < 2ζ时为±0dB/dec保持;Ω > 2ζ时以-40dB/dec减少。
(8) 电感的功率在Ω < 2ζ时以+20dB/dec增加;Ω > 2ζ时以-20dB/dec减弱。
(9) 电容的功率在全频率内均为+20dB/dec。
(10) 电源的功率为SR、SL与SC三者中的最大值;但在Ω = 1且ζ < 0.5时,功率明显低于SL和SC并且几乎与SR相等。
(11) ζ主要对转折频率以下的IR、SR和SL产生较大的影响;重点影响Is和Ss在Ω = 1附近的行为。
(12) 由于并联电路电压相等,因此使用电压源驱动RLC并联电路,元件响应仅为一阶;该电路的二阶响应主要在Is和Ss上体现。该电路大部分的应用为降低电源的电流以及视在功。
将以上部分规律总结为表格
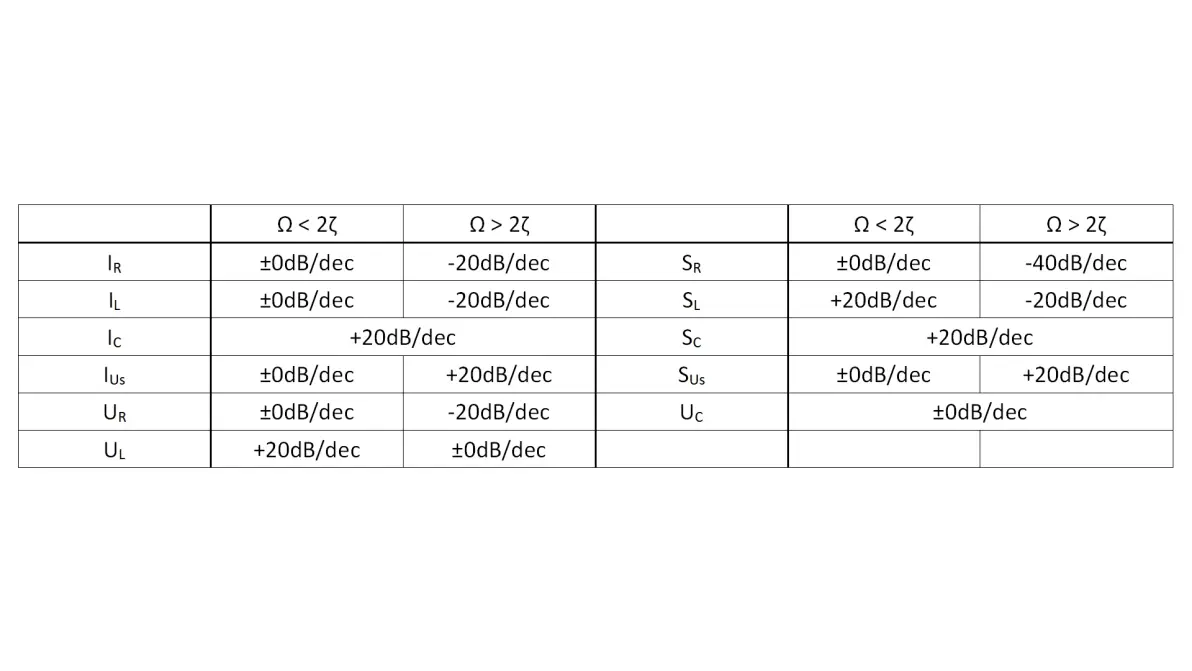
图2.24:RLC并联电路正弦电压激励部分规律
3、正弦电流源驱动的RLC并联电路
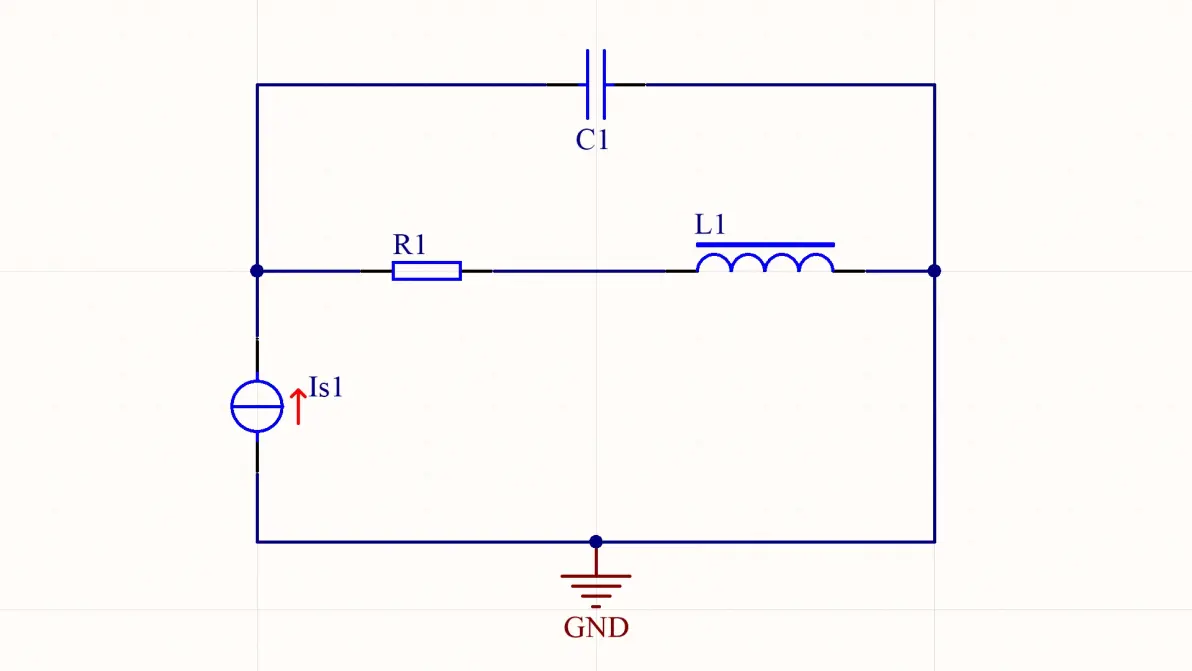
图3.1:电流源驱动的RLC并联电路
3.1 公式
符号定义同第1章
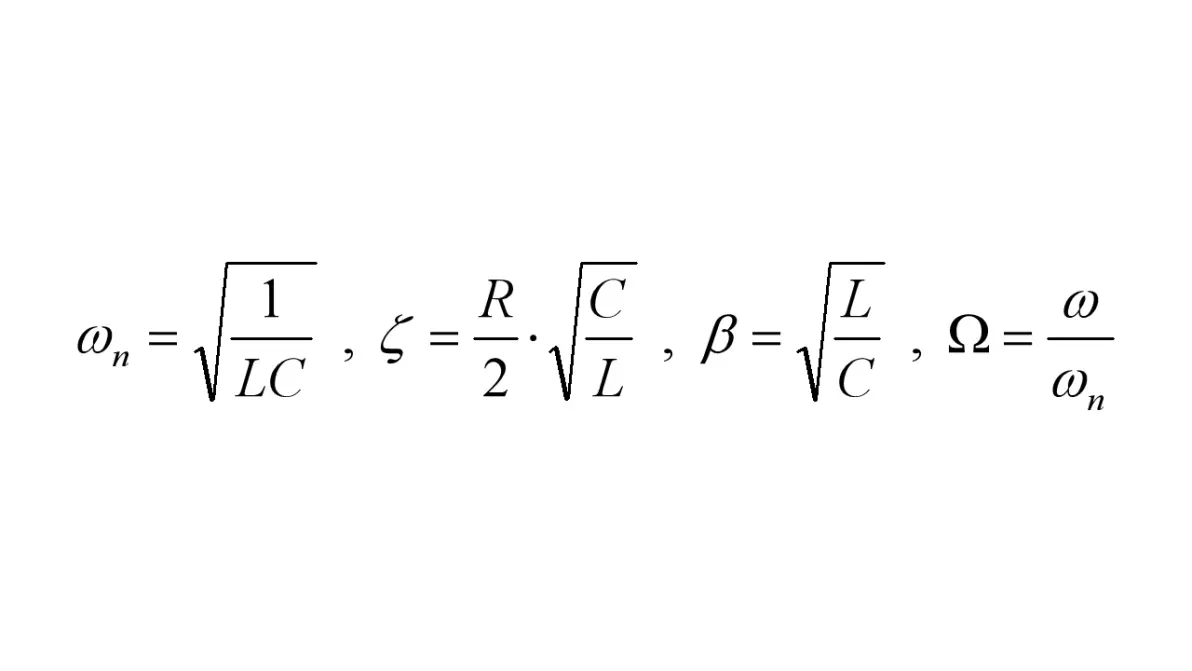
图3.2:符号定义
该电路拥有两个节点和两个支路,拥有三个拓扑约束:uC = uR+uL,iR = iL,iIs = iL+iC,相互解算得出各元件的电流和电压,先给出各元件电流有效值(Irms)(元件已达到稳态)
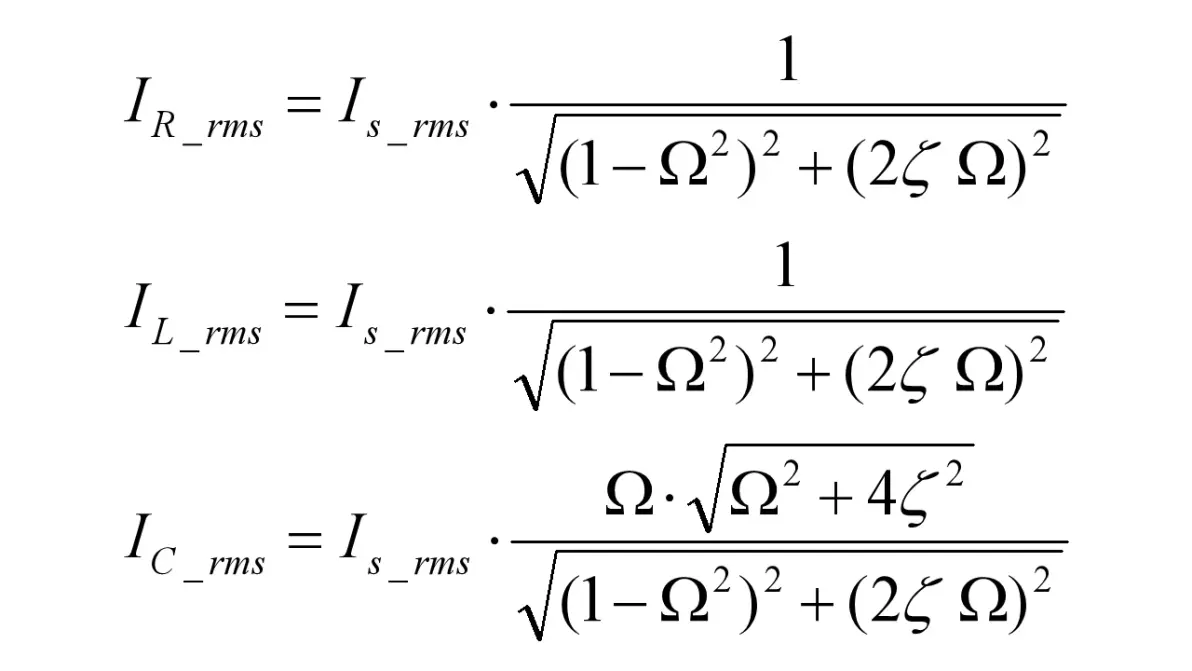
图3.3:RLC并联电路正弦电流激励元件电流
元件的电压有效值(Urms)为
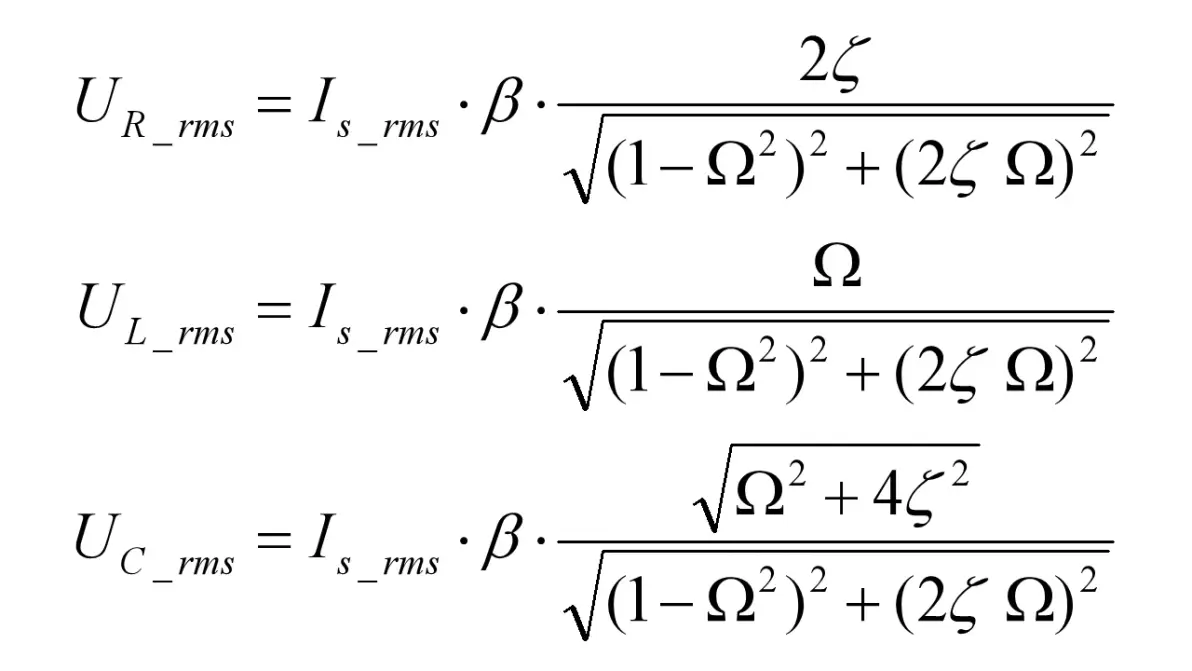
图3.4:RLC并联电路正弦电流激励元件电压
RLC三种元件和激励源的视在功率(S)为
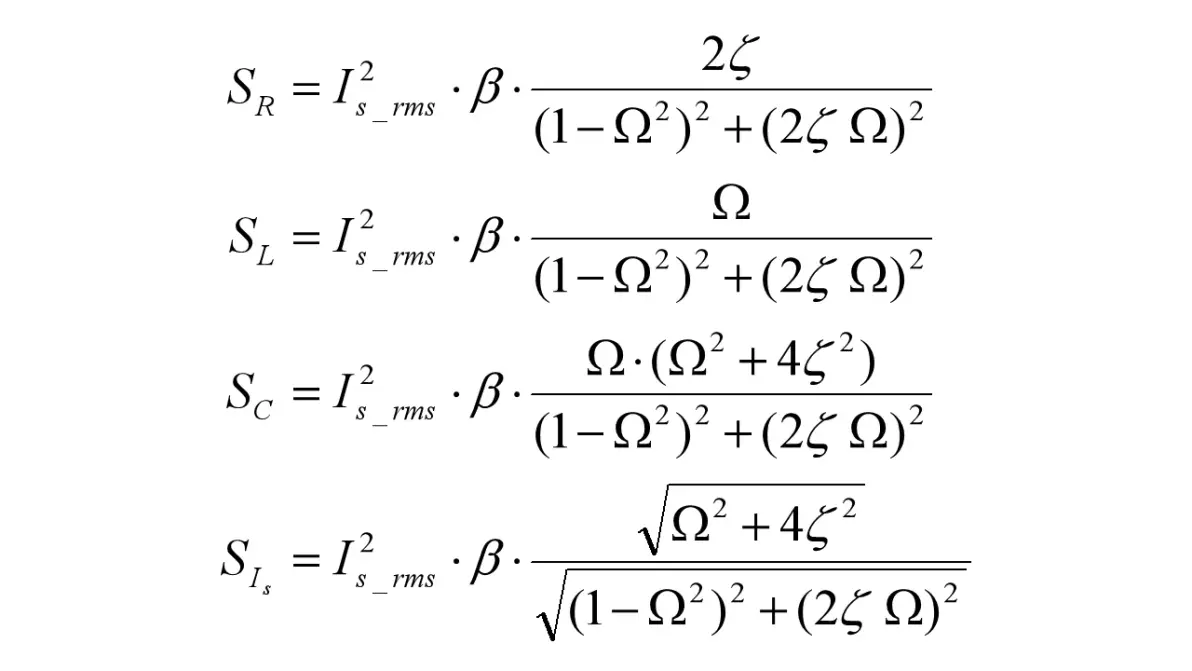
图3.5:RLC并联电路正弦电流激励元件视在功率
3.2 图像
将以上公式绘制成图像,由于ζ的不同会导致图像某些部分差异巨大,因此分别选取ζ = {0.088, 0.250, 0.500, 0.707, 1.414, 4.000}进行作图。以下为元件电流(Irms)图像
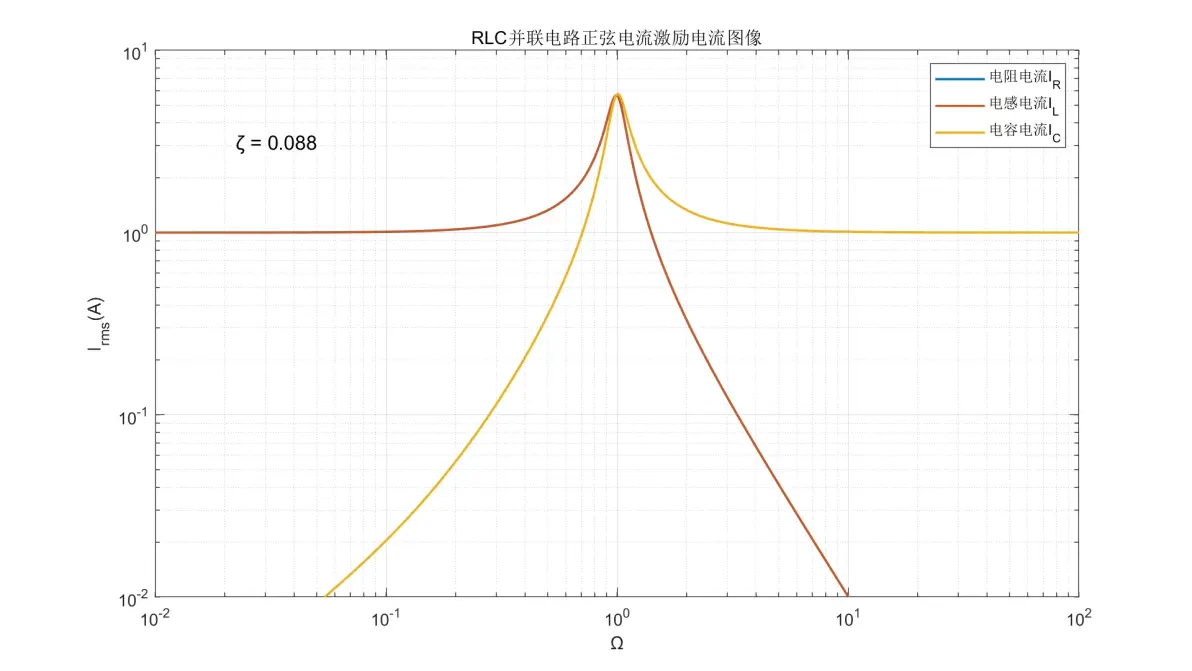
图3.6:RLC并联电路正弦电流激励元件电流图像(ζ = 0.088)
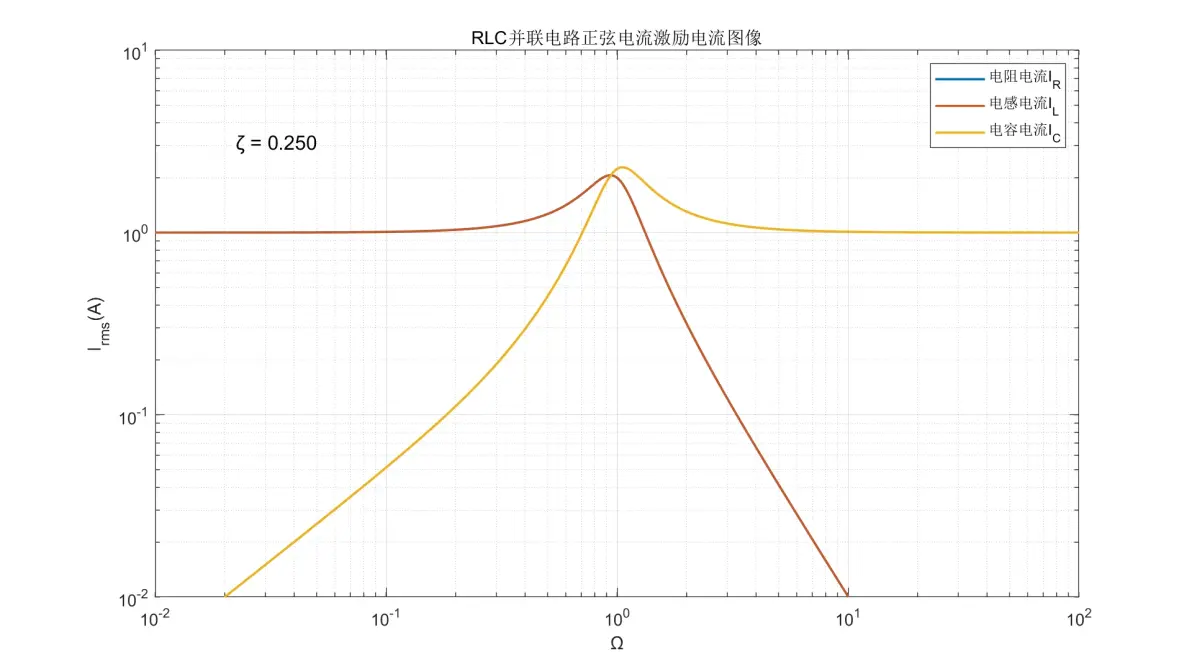
图3.7:RLC并联电路正弦电流激励元件电流图像(ζ = 0.250)
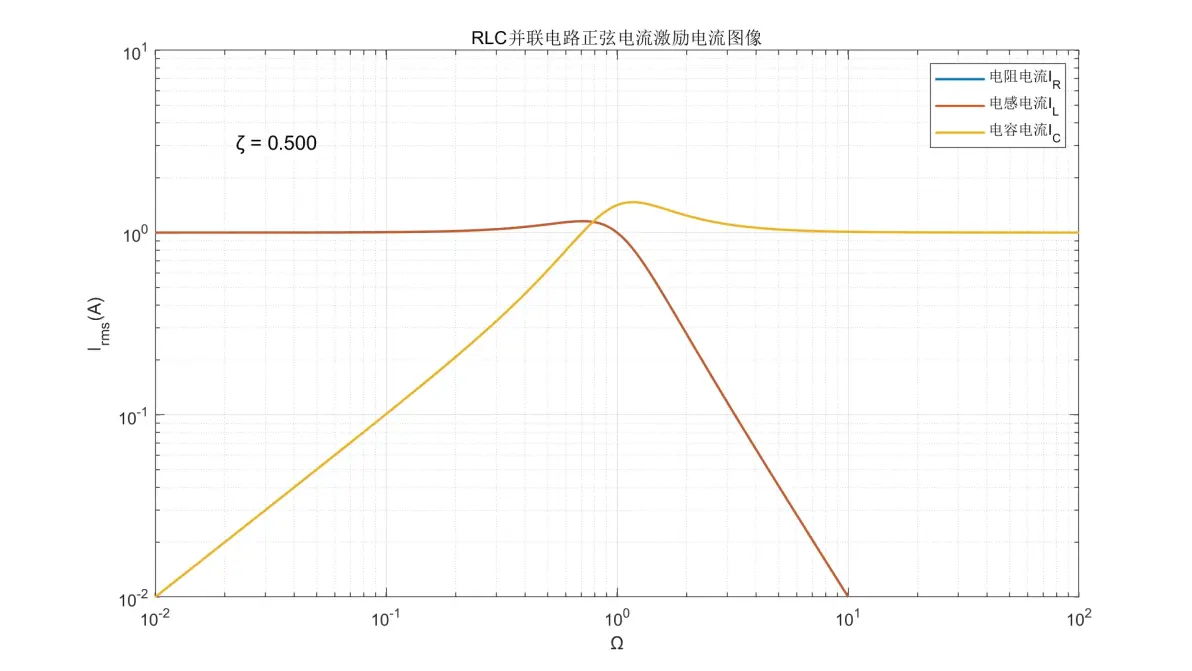
图3.8:RLC并联电路正弦电流激励元件电流图像(ζ = 0.500)
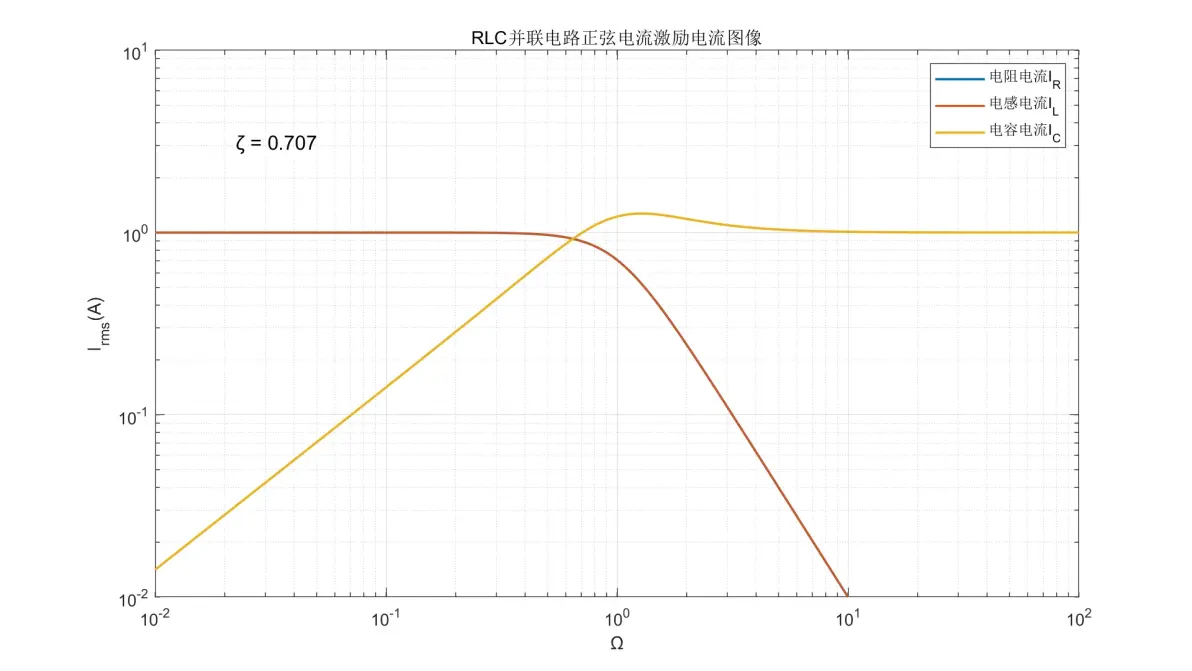
图3.9:RLC并联电路正弦电流激励元件电流图像(ζ = 0.707)
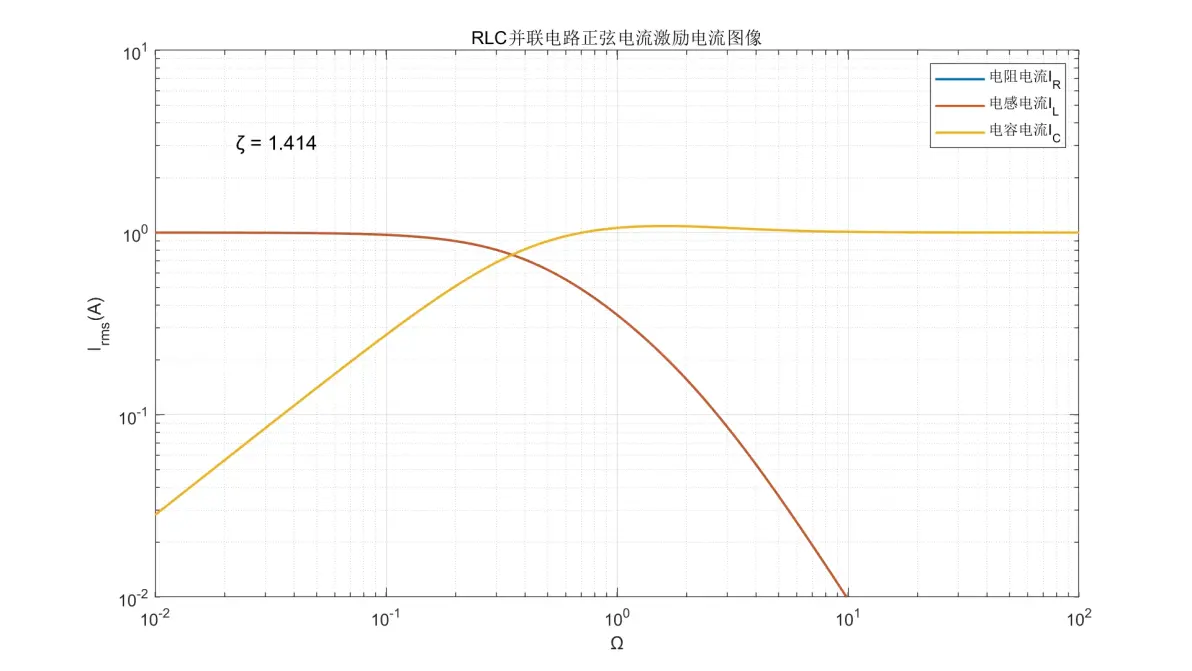
图3.10:RLC并联电路正弦电流激励元件电流图像(ζ = 1.414)
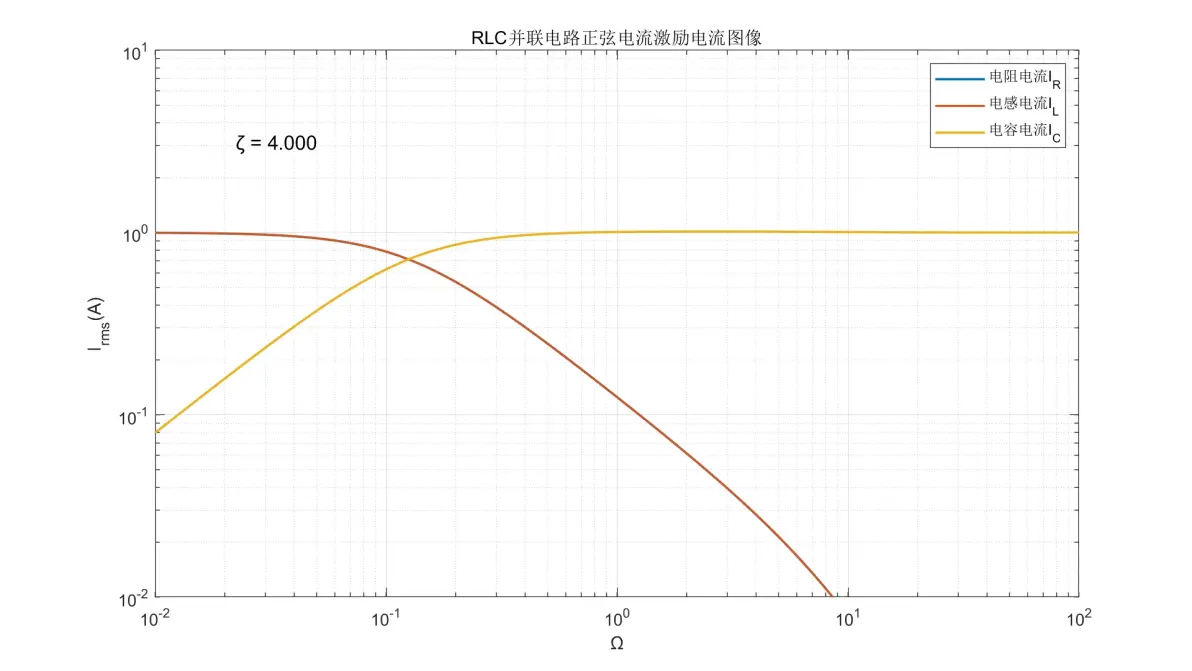
图3.11:RLC并联电路正弦电流激励元件电流图像(ζ = 4.000)
以下为元件电压(Urms)图像
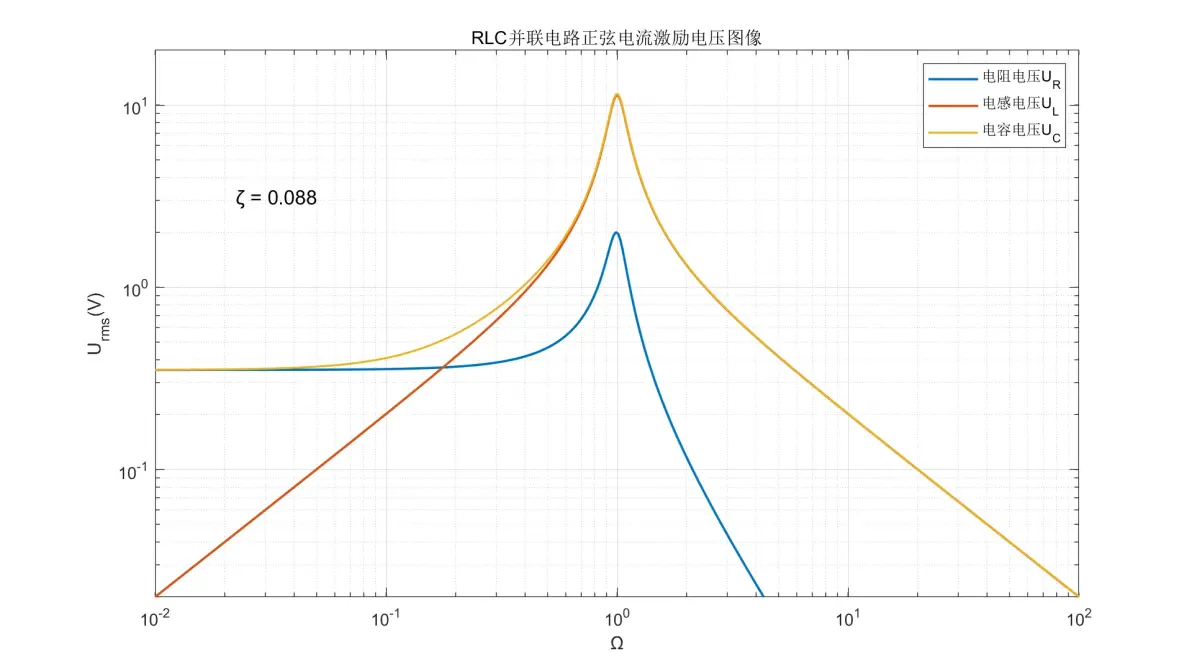
图3.12:RLC并联电路正弦电流激励元件电压图像(ζ = 0.088)
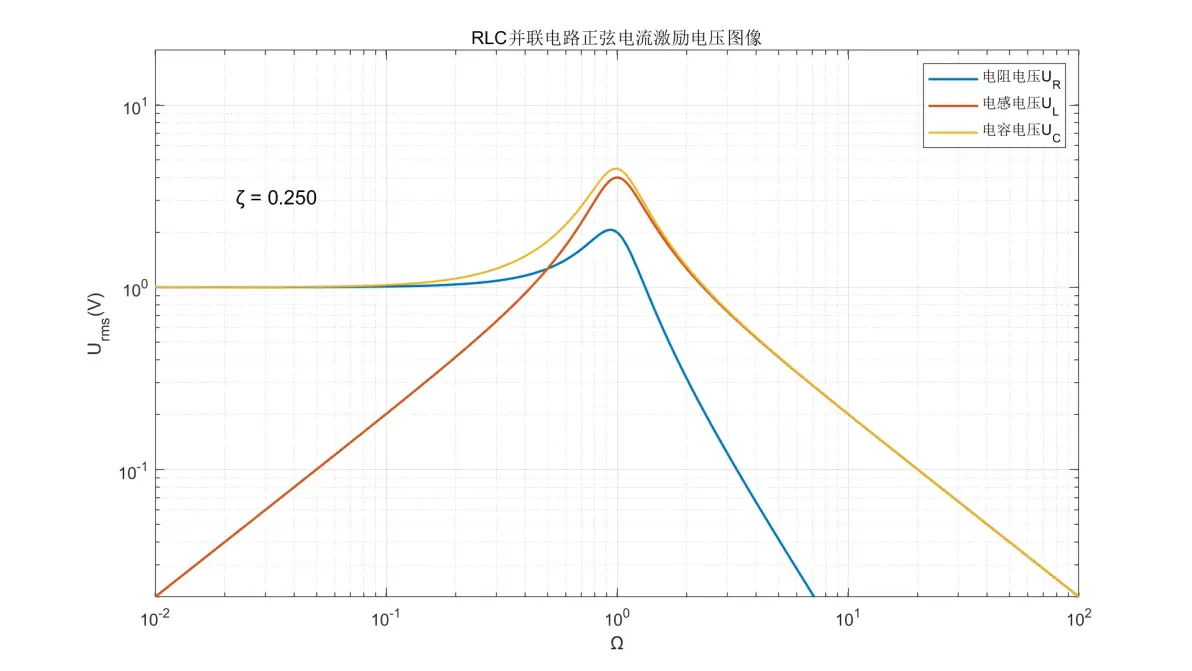
图3.13:RLC并联电路正弦电流激励元件电压图像(ζ = 0.250)
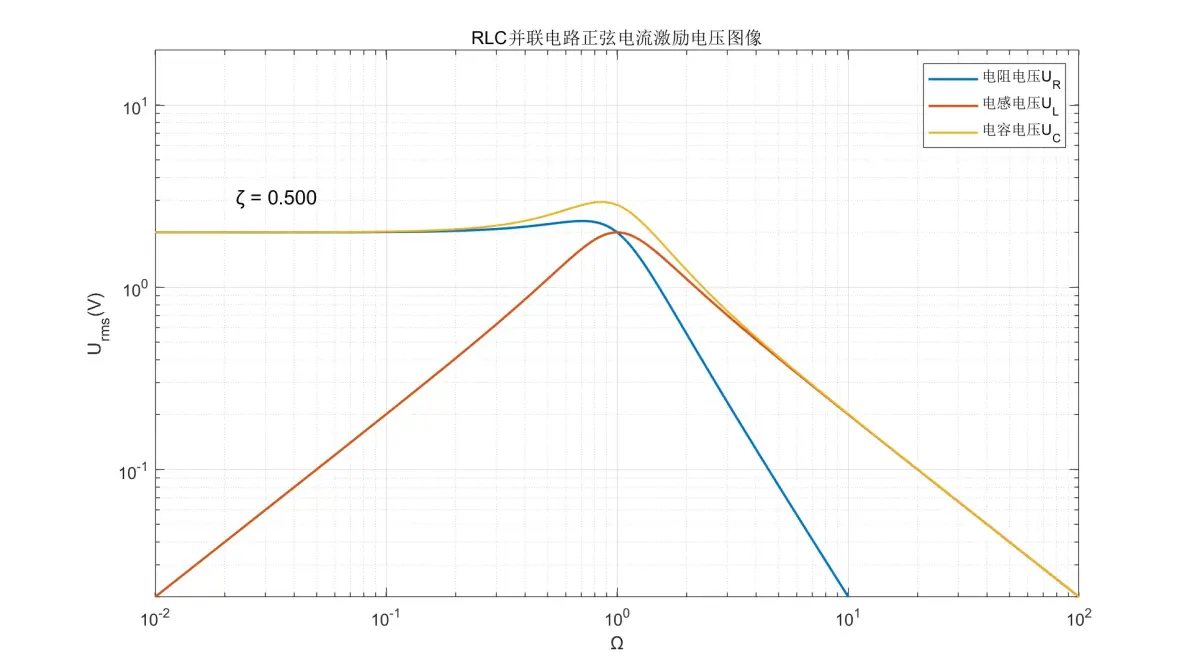
图3.14:RLC并联电路正弦电流激励元件电压图像(ζ = 0.500)
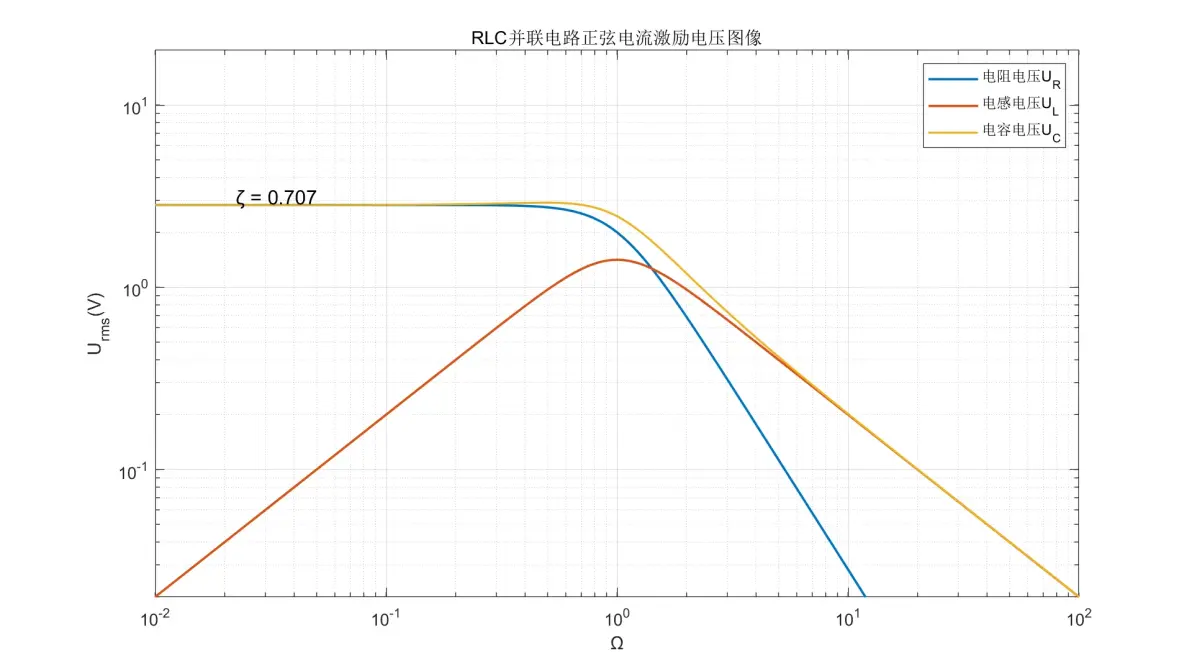
图3.15:RLC并联电路正弦电流激励元件电压图像(ζ = 0.707)
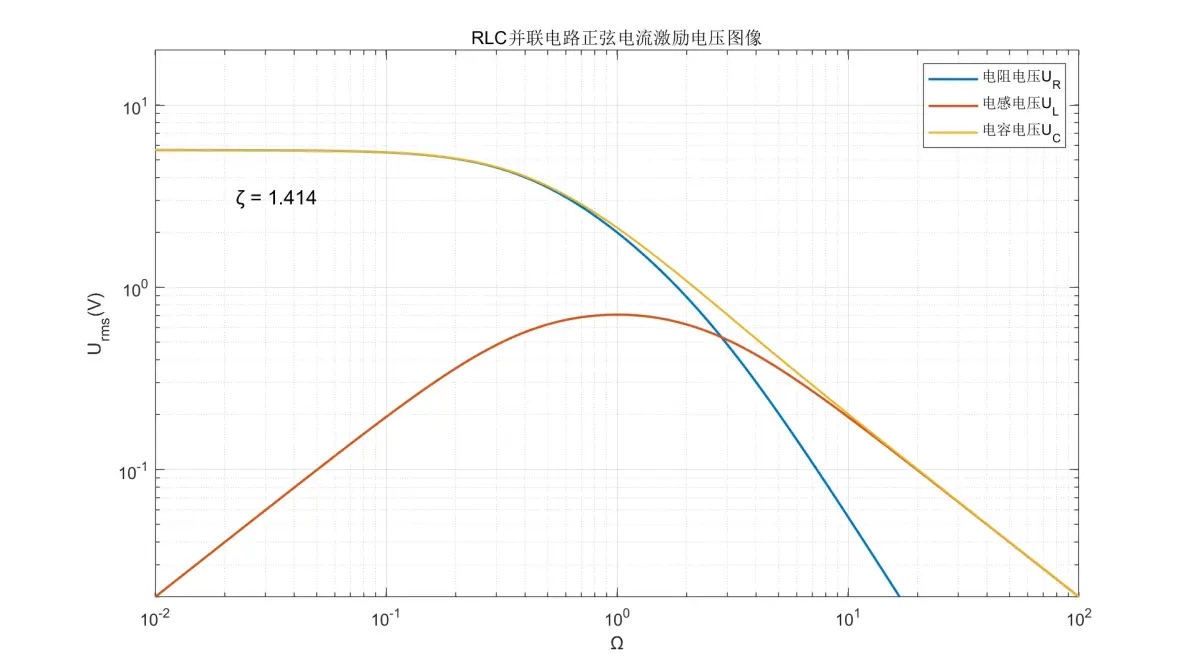
图3.16:RLC并联电路正弦电流激励元件电压图像(ζ = 1.414)
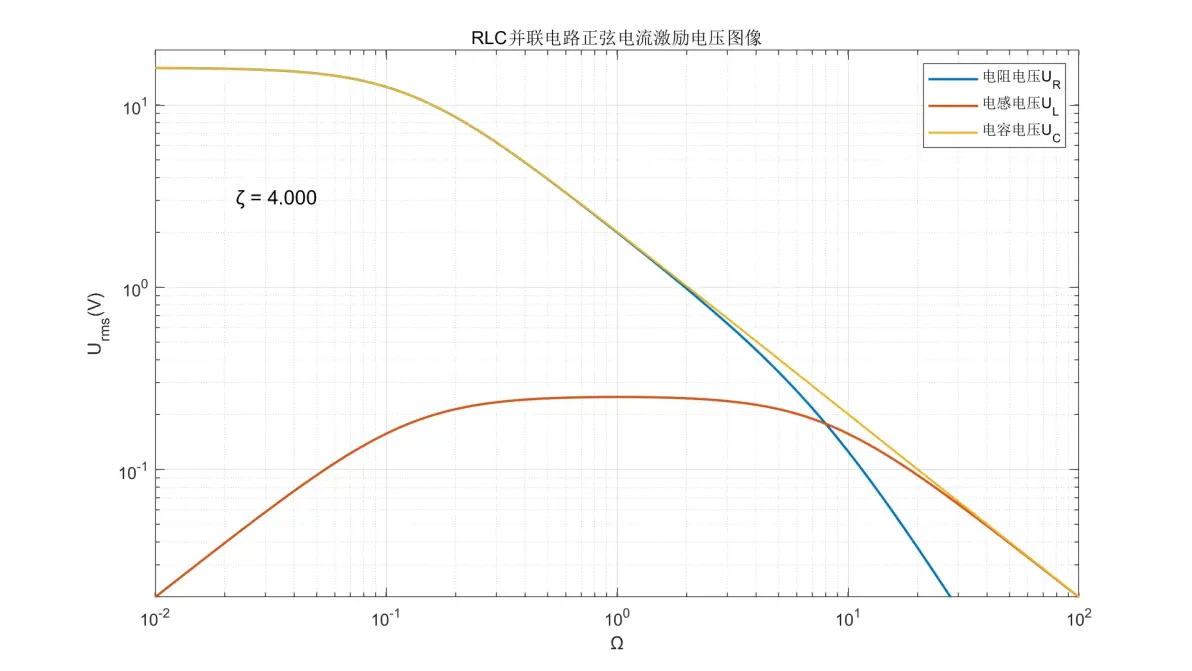
图3.17:RLC并联电路正弦电流激励元件电压图像(ζ = 4.000)
以下为元件功率(S)图像
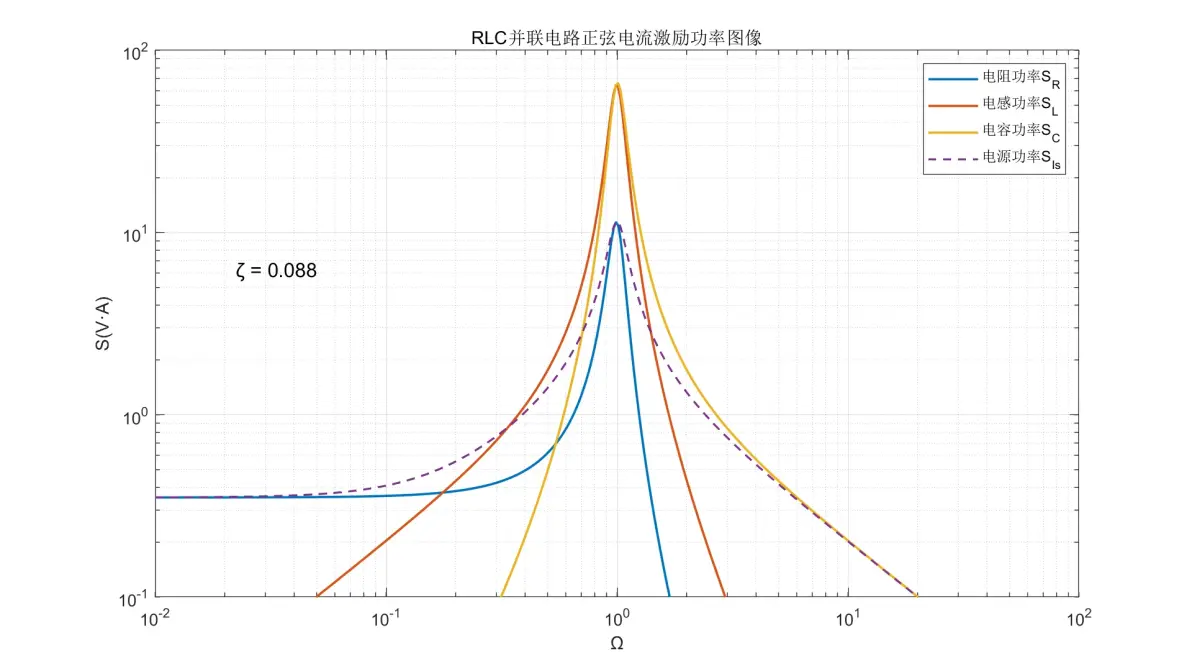
图3.18:RLC并联电路正弦电流激励元件功率图像(ζ = 0.088)
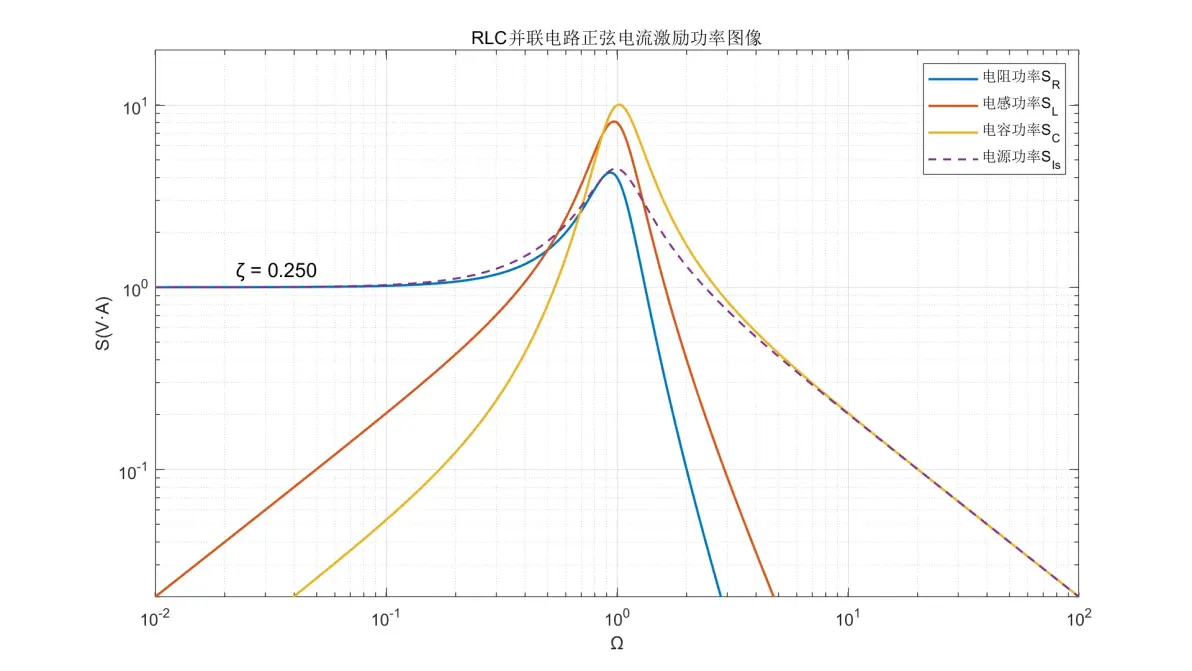
图3.19:RLC并联电路正弦电流激励元件功率图像(ζ = 0.250)
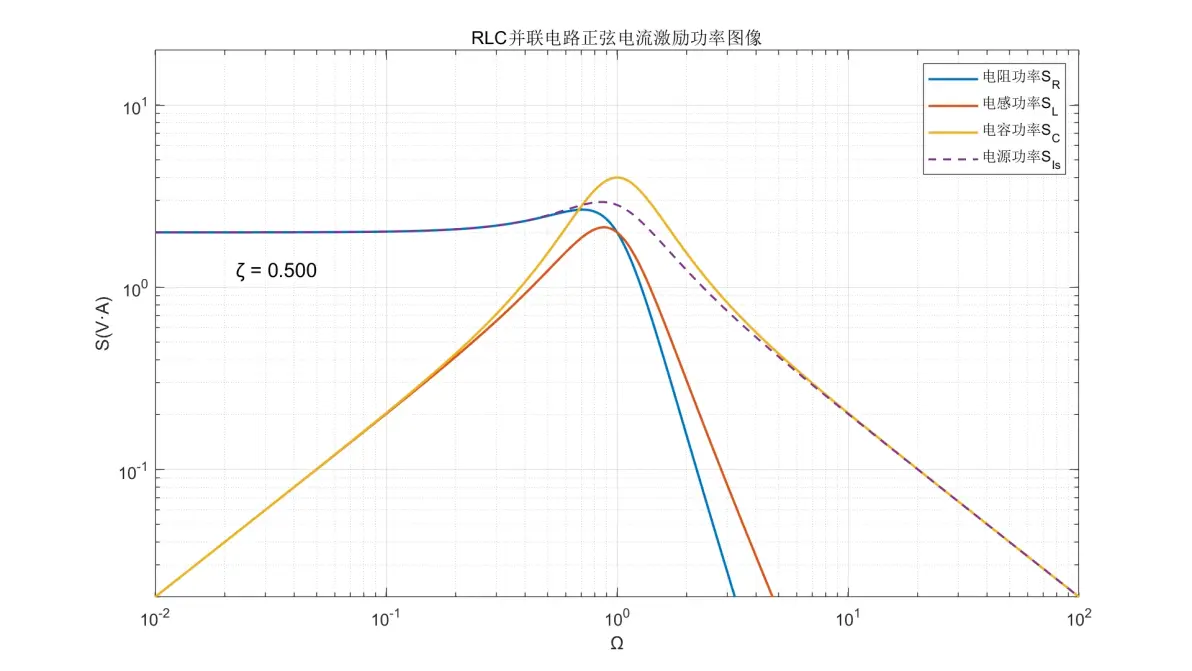
图3.20:RLC并联电路正弦电流激励元件功率图像(ζ = 0.500)
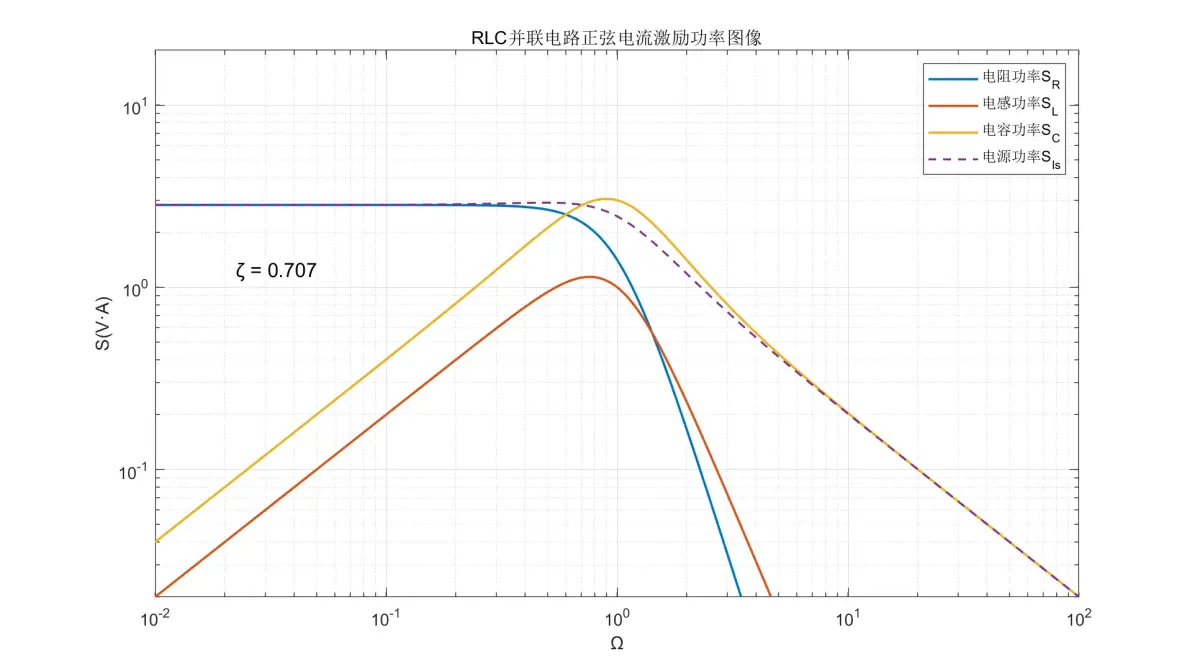
图3.21:RLC并联电路正弦电流激励元件功率图像(ζ = 0.707)

图3.22:RLC并联电路正弦电流激励元件功率图像(ζ = 1.414)
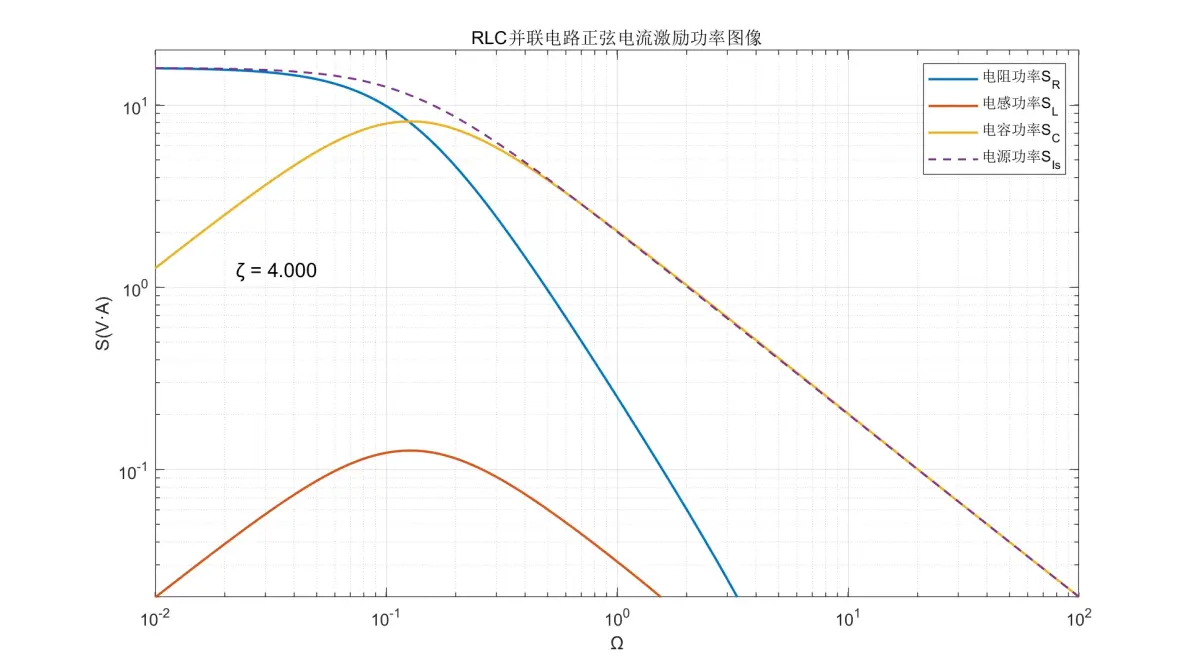
图3.23:RLC并联电路正弦电流激励元件功率图像(ζ = 4.000)
3.3 规律总结
(1) 电阻和电感的电流是同一个,在Ω < 1时为±0dB/dec;Ω > 1时则以-40dB/dec的速率减弱;Ω = 1附近的行为取决于ζ。
(2) 电容的电流在Ω < 1流为+20dB/dec;Ω > 1时则变为±0dB/dec;Ω = 1附近的行为取决于ζ。注意IC与IR、IL的行为并不完全对称。
(3) 电阻的电压变化规律与IR一致。
(4) 电感的电压在Ω < 1时为+20dB/dec;Ω > 1时为-20dB/dec;Ω = 1附近的行为取决于ζ。
(5) 电容的电压在低频时为±0dB/dec;高频时为-20dB/dec。
(6) 电阻的功率在低频时为±0dB/dec;高频时为-80dB/dec。
(7) 电感的功率在低频时为+20dB/dec;高频时为-60dB/dec。
(8) 电容的功率在低频时为+20dB/dec;高频时为-20dB/dec。
(9) 电源的功率在低频时为±0dB/dec;高频时为-20dB/dec。
(10) 由于使用电流源激励,ζ的增大均会增加UR和SR,其同时增加低频区域的UC和SC,对UL和SL的影响主要在Ω = 1附近的行为。
(11) RLC并联电路正弦电流激励,与RLC串联电路正弦电压激励相互对偶,因此电压与电流角色互换,因此规律也接近互换。但由于R和L是串联关系(现实中这种情况更为常见),电路并不是完全对偶,所以在低频区特性并不完全等于RLC串联电路。
将以上部分规律总结为表格
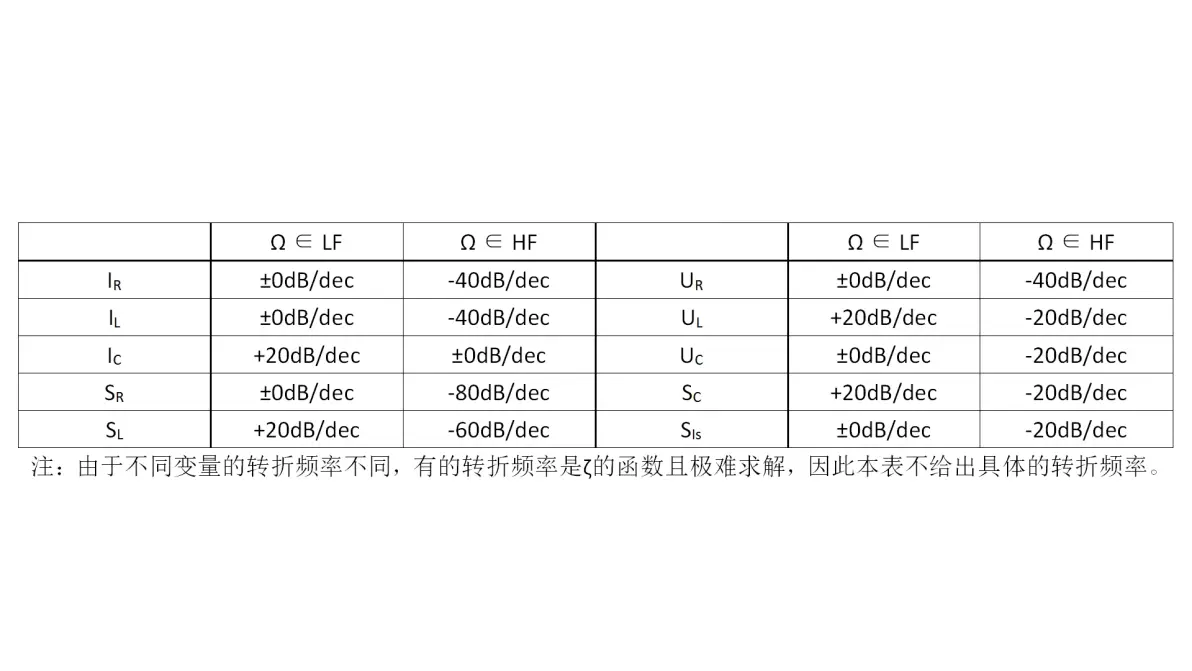
图3.24:RLC并联电路正弦电流激励部分规律

后记
公式全部亲自推导并使用MATLAB仿真以验证其正确性。
使用Altium Designer绘制电路图,MATLAB绘制函数图。
by HD-nuke8800
2023/10/14