写在前面
唔,这是我在学习数模过程中的一些感触,在国赛三天时间内接触一个全新的领域,并解答出一个社会问题,如果真的想理解每个公式每个定理的含义,这好像。。比三天学完一本药理学还难啊,所以老师上课时候提到一个观点,在某些时候“不求甚解”,比赛期间只要知道这样做能得到什么结果,并且这个结果是用来干什么的,能够证明什么,就好啦。所以这篇文章前半段讲得到什么结果以及作用,在其中穿插用五一数模第五题作为实例来介绍,文末附全部代码,同时,我也会在日后补上视频介绍。
而在论文里面,那种定理的证明与公式部分,网上,CSDN上面很多很多,所以阅卷老师也不会很认真地去看,只要整体卷面比较整洁就好啦。
我本身能力属实有限,写这个文章也只是记录一下学习过程,如果有讲得不好的地方请大家海涵,希望我们都能够在九月份的数模国赛中拿到一个比较好的奖项,我们一起努力!
时间序列分析与预测
时间序列分析首先要确定是时间序列,可以理解为横坐标为时间,纵坐标为随着时间变化某个值也随之变化的数据序列
时间序列分析主要分为:
平稳性检验
一个数列所有的统计性质都不会随着时间的推移而发生变化的时候,就是说明数据是平稳的,例如某段时间某物产量图:

呈现上升趋势,不平稳,而只有在数据是平稳的条件下,对数据的预测与后续处理才是可靠的,不然大家想,时间变化的同时,数据也在变化,那预测不了,只有时间变化的时候,呈现平稳,才是可预测的。
所以需要使用单位根检验方法,其中最为常用的就是ADF检验,例如五一数模Q5让我们预测后八周的数据,我首先对前几周的数据进行ADF检验,判断是否平稳。(通过使用matlab中的adftest函数来进行检验,返回1,序列平稳,范返回0,序列不平稳)

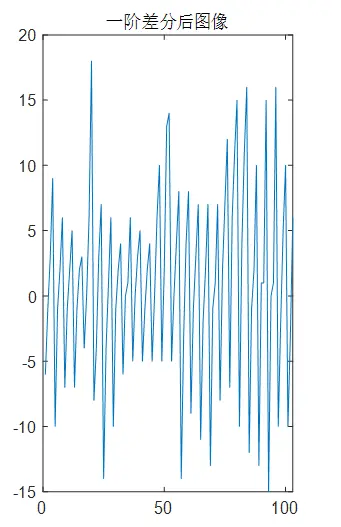
刚开始序列不平稳,返回了0,我看这个图像,整体呈现上升的趋势,如果有趋势,通过阶分消除趋势,如果存在周期,例如一天中的温度变化,那就使用步差分消除周期,我在使用一阶差分之后得到一个平稳的序列
白噪声检验
我把它理解判断是不是“没用数据”,因为如果数据是有用的,前后是要有联系的,如果没有联系,没有信息传递,那这段数据是没用的。
噪声有什么特点?就是“随机的,嘈杂的”,如果数据都是“随机的”,那这段数据对我们的数据预测还有什么用呢。
判断其LB统计量,如果想知道原理可以去网上查一下,这个我没学过,我只会用,看其P值,如果P值小于0.05,那为非白噪声序列。

我对这些数据进行分析之后发现,P值都接近0,因此均为非白噪声序列(实际上肯定不是0,只是因为太接近0了,低于matlab的最低精度)
模型识别
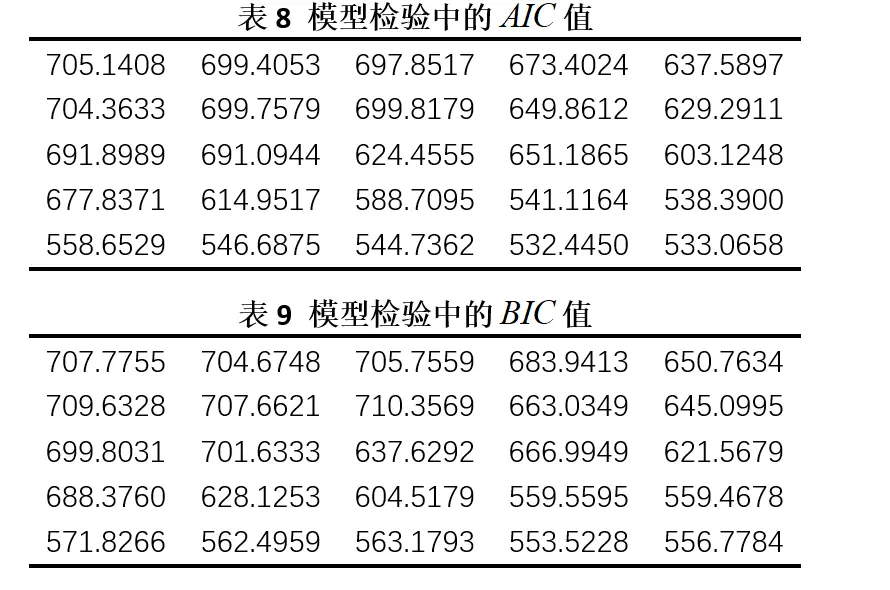
我当时学的时候,其实整体没听懂,连公式都看不懂,就是抓住两个重点,一个是似然函数值越大越好,另一个是未知参数越少越好,根据代码得到的结果,找出AIC值最小的左边,注意是从0开始,例如常规认为的(1,1)需要输入(2,2),也即是p=2,q=2。
例如五一数模中的Q5,我当时得到这两个表,然后AIC最小值是532.4450,坐标为(4,3)
进而可以得到该模型数据信息为:

模型检验
为了检验模型对整体序列的信息提取是否完全,通过检验残差,我理解为“检验不在模型中的数据为没用的数据”,大家想,如果不在模型中的数据都已经确定是没用的“噪声序列”,而在模型识别中已经把数列中的数据尽可能放入模型中了,因此从正反两个方面都说明了模型很适合最后额结果。

第五题代码
function Q5_time()
%Q5_PWXJY 对第1周到第104周的数据进行平稳性检验
% 时间序列预测 step 1
% 发现数据不是平稳的,就要通过差分的方法将数据变为平稳
% 阶差分消除趋势,步差分消除周期
clc;
clear;
%% 数据的输入与预定义
temp_data = xlsread('data_5', 1, 'A1 : H13');
data = zeros(1, 104);
for i = 1 : 13
temp = temp_data(i, :);
data(:, (8 * (i - 1) + 1 : 8 * i)) = temp;
end
%% 进行平稳性检验
t_1 = (1 : 104)';
subplot(1, 2, 1);
plot(t_1, data);
title('原始数据时序图');
disp(adftest(data));
%% 利用一阶差分消除趋势
t_2 = (1 : 103)';
x1 = diff(data);
subplot(1, 2, 2);
plot(t_2, x1);
title('一阶差分后图像')
disp(adftest(x1));
%% 白噪声检验
yanchi = [6, 12, 18];
[~, pValue, Qstat, ~] = lbqtest(x1, 'lags', yanchi);
%按表格形式打印相应统计量
fprintf('%15s%15s%15s','延迟阶数','卡方统计量','p值');
fprintf('\n');
for i=1:length(yanchi)
fprintf('%18f%19f%19f',yanchi(i),Qstat(i),pValue(i));
fprintf('\n');
end
%% temp
s = 12;
m1=length(x1);
for i=s+1:m1
y(i-s)=data(i)-data(i-s);
end
%% 模型识别
n = 8; % 令对象数量限制在8个里面
m2=length(x1);
x1=x1';
LOGL = zeros(5,5);% Initialize
PQ = zeros(5,5);
for p = 0:4
for q = 0:4
model=arima(p,0,q);%指定模型的结构
[~,~,logL] =estimate(model,x1); %拟合参数
LOGL(p+1,q+1) = logL;
PQ(p+1,q+1) = p+q;%计算拟合参数的个数
end
end
LOGL = reshape(LOGL,numel(LOGL),1);
PQ = reshape(PQ,numel(PQ),1);
[aic,bic] = aicbic(LOGL,PQ+1,m2);
fprintf('AIC为:\n'); %显示计算结果
reshape(aic,5,5) %储存25个模型AIC的值
fprintf('BIC为:\n');
reshape(bic,5,5) %储存25个模型BIC的值
%% 模型估计
p=input('输入阶数p=');q=input('输入阶数q=');
model=arima(p,0,q); %指定模型的结构
m=estimate(model,x1) %拟合参数
%% 模型残差检验
z=iddata(x1);
ml1=armax(z,[p,q]);
e = resid(ml1,z);%拟合做残差分析
[H,pValue,Qstat,CriticalValue]=lbqtest(e.OutputData)
%% 模型预测
[yf,ymse]=forecast(m,n,'Y0',x1);%yf为x1预测值
yhat=y(end)+cumsum(yf)%求y的预报值
for j=1:n
x(m1+j)=yhat(j)+data(m1+j-s);%求x的预测值
end
xhat=x(m1+1:end)%截取n个预报值
end