【NOTE: 本代码不涉及题目求解方法,仅作为MATLAB三维图形可视化的一次探索】
本次国赛虽然没参赛,但作为一个老数模玩家(A题限定)为了好玩写了个2021年FAST反射面可视化程序。虽然里面还不含动画、求解问题的算法,但就仅仅为了探索MATLAB的三维可视化效率,大家看个乐。
所以本文的重点仅仅是总结MATLAB的一些使用技巧了(题目模型和求解有缘再来做,个人觉得本题核心还是求解和程序困难,模型部分比较简单)。先上个效果图,
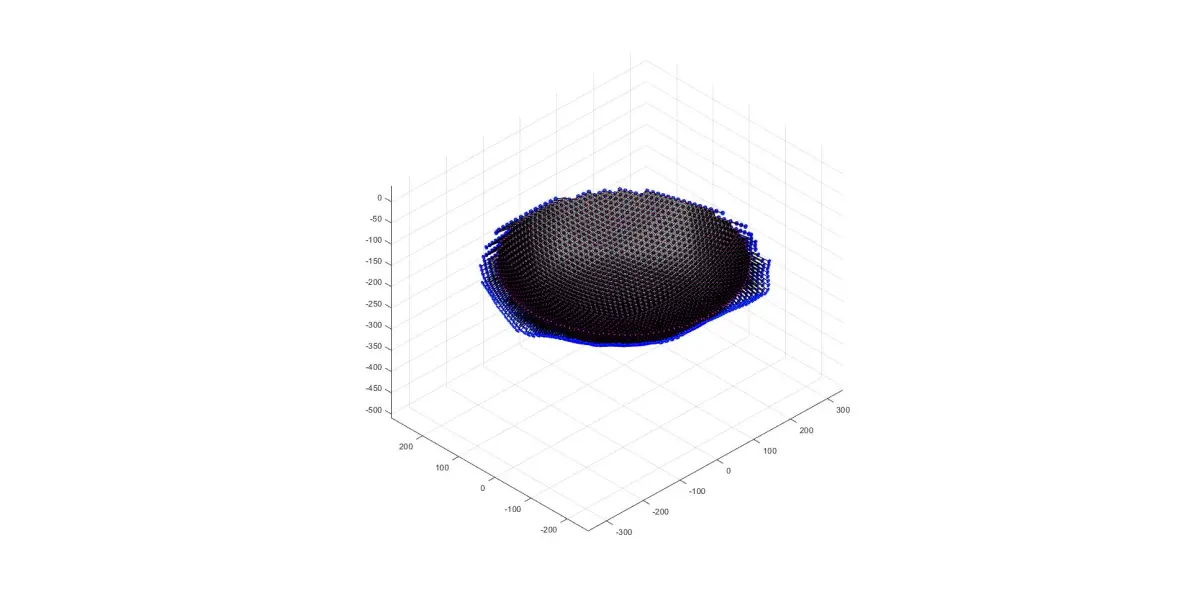
整体图(正面)
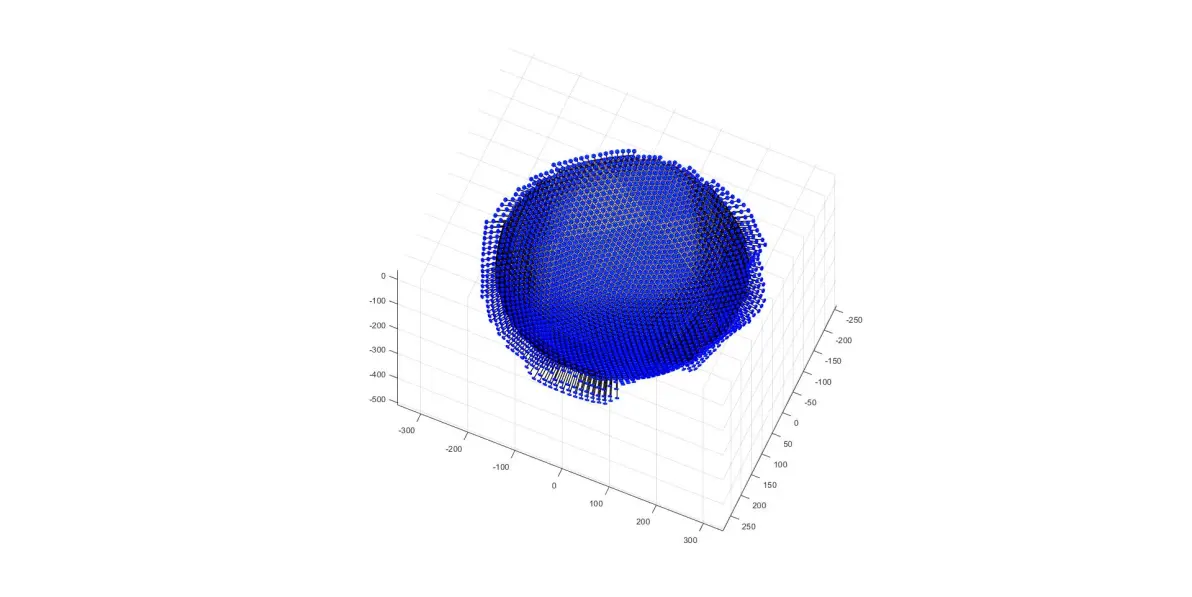
整体图(反面)
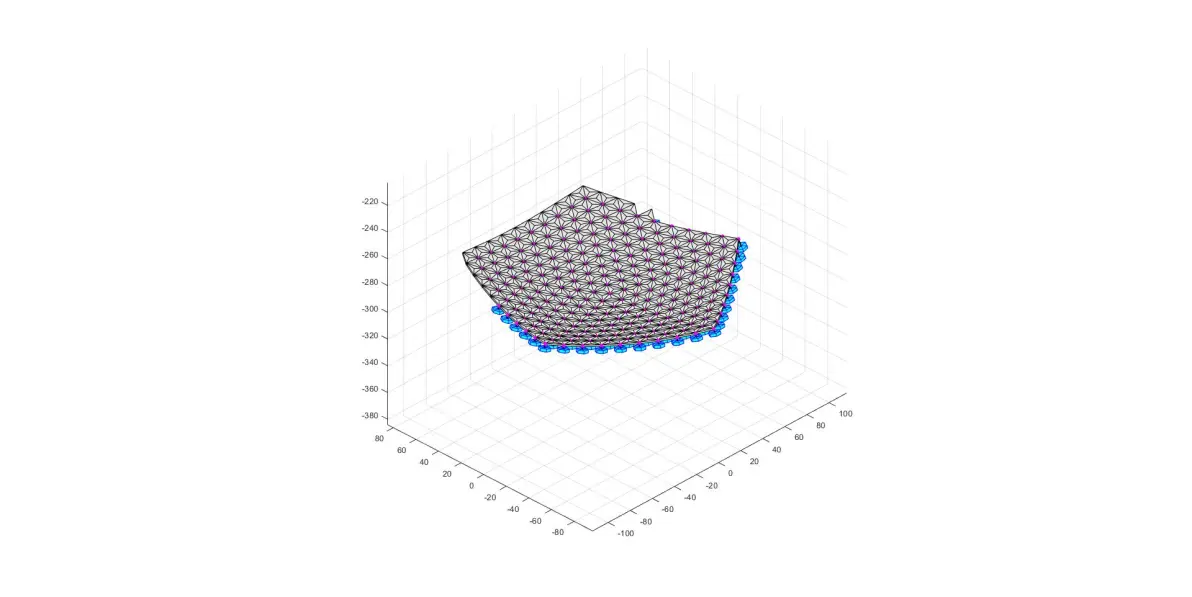
局部图(正面)

局部图(反面)
核心代码下载:https://pan.baidu.com/s/1Mj4_3uj0x4m5-UWGh7zjpw
提取码:dinn

Q1:surf()/mesh()函数原理?
A1:输入的X,Y,Z矩阵每行用线连接,行和行之间取依次取3*2个点画面(且不会自动循环)。因此,如果你要画一个封闭的正三棱柱,可能要输入6+3个点(补充循环以保证封闭),和在首行和尾行补充一个上下底面中的点(比如中点),才能保证5个面的封闭性,如在MyNormTriPrismModel.m里,我的做法是,
X = [ones(1, 4)*this.Center(1) + 0.5*this.Height.*this.Orientation(1);
[this.Parameters(1:3, 1)', this.Parameters(1, 1)] + 0.5*this.Height.*this.Orientation(1);
[this.Parameters(1:3, 1)', this.Parameters(1, 1) ]- 0.5*this.Height.*this.Orientation(1);
ones(1, 4)*this.Center(1) - 0.5*this.Height.*this.Orientation(1)];
Y = [ones(1, 4)*this.Center(2) + 0.5*this.Height.*this.Orientation(2)
[this.Parameters(1:3, 2)', this.Parameters(1, 2)] + 0.5*this.Height.*this.Orientation(2);
[this.Parameters(1:3, 2)', this.Parameters(1, 2)] - 0.5*this.Height.*this.Orientation(2);
ones(1, 4)*this.Center(2) - 0.5*this.Height.*this.Orientation(2)];
Z = [ones(1, 4)*this.Center(3) + 0.5*this.Height.*this.Orientation(3)
[this.Parameters(1:3, 3)', this.Parameters(1, 3)] + 0.5*this.Height.*this.Orientation(3);
[this.Parameters(1:3, 3)', this.Parameters(1, 3)] - 0.5*this.Height.*this.Orientation(3);
ones(1, 4)*this.Center(3) - 0.5*this.Height.*this.Orientation(3)];一个例子是,
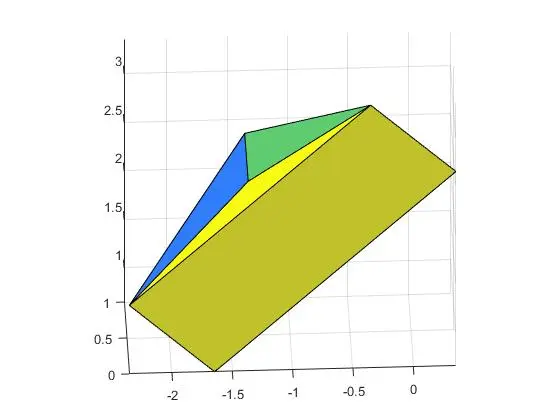
这种方法不需要进行坐标变换,当然这也是图形的特殊性导致的。相比用我魔改的官方文件CylinderModel.m的MyCylinderModel.m,就不得不使用坐标变化来实现任意圆柱的绘制了。
Q2:MATLAB绘制大量(三维)图形为什么这么慢,如何尽可能优化?
A2:经过我的测试,MATLAB图形绘制最费时的部分是对图形句柄的创建上(如此例中的surf图形对象)。所以一种优化方法是,使用cell预先存储大量的surf对象待用(如先存在.mat中),当需要使用时直接分配这些surf对象的X,Y,ZData和Parent句柄即可。通过这样的方法,我把上述有1W多个对象的图像句柄图像,在2s左右就能显示出来(当然运行前load对象用了了将近1分钟,但这是值得的,因为我们只需要载入一次对象,就能在接下来的渲染中不断复用了),在本代码当中,是这么做的,
保存句柄(ShowProcess参见上一篇专栏):
clc
clear
N = 10000;
sh = ShowProcess(N, 1);
PLS = cell(N, 1);
for i = 1 : N
sh.tic(i);
PLS{i} = surf([], [], []);
hold on;
sh.toc(i);
end
% save("PreLoadSurf.mat", "PLS");加载句柄:
clc
clear var -except PLS
close all
global PLS
if isempty(PLS)
load("PreLoadSurf.mat");
end
FastModel = FAST(PLS);当然,如果你直接保存这些句柄,那么大概率你会在再次使用这些句柄时遇到类似“对象无效或已删除。”的报错。为此,请查看下一个问题。
Q3:如何在关闭Figure后避免Figure上的对象自动删除?
A3:MATLAB设定当Figure关闭后,以上所有Children都自动删除。为了避免这点,我们需要先把这些对象的Parent指向别处(如[]),最方便的做法是在Figure的DeleteFcn回调函数里写,
function fig_exit(obj, h, event)
N = length(obj.PlotHandleBuffer);
for i = 1 : N
obj.PlotHandleBuffer{i}.Parent = [];
end
end(注以上代码是在类函数,obj是指本类,h和event是本来回调函数里对应的handle和event对象,如果你在非类里面写,可能需要通过global等方式把你存储的那一堆图像句柄读进来分别改变它们的Parent属性。)
Q4:如何实现坐标变换?
A4:简单的线性代数知识告诉我们,对于同一个向量在两组基矩阵B1,B2的坐标C1,C2满足,
于是,你只需要对对应的基矩阵取逆即可。求得基矩阵的方法是,在同一坐标系下表示出B1,B2基下的单位方向向量,按列向量填入B1或B2矩阵即可。设B1为标准正交基矩阵,且在三维情况下就是,
由于上述仅代表了线性变化,如果增加了原点的平移,即仿射变换,上面的关系式就可以表达成,

暂时先写这么多。总得来说,虽然通过预缓存极大提高了MATLAB的绘图效率,但通过MATLAB拖拽互动的效率仍十分卡顿。毕竟MATLAB作为科学计算软件还是有极限的。。。所以是不是应该学点其他的专业引擎做模型可视化了(