MATLAB求解线性规划模型：投资收益与风险案例分析

关注公众号：数学建模BOOM，回复“线性规划”，领取matlab代码文件；

例题：投资收益与风险

题目出自《数学建模算法与应用（第2版）》第6页；

• 市场上有n种资产𝑠_𝑖 (𝑖 = 1,2,…,n)，用数额为M的资金作一个时期的投资；
• 这n种资产在这一时期内购买𝑠_𝑖的平均收益率为𝑟_𝑖，风险损失率为𝑞_𝑖；
• 投资越分散总的风险越少，总体风险用投资的𝑠_𝑖中最大的风险来度量；
• 购买𝑠_𝑖时要付交易费，费率为𝑝_𝑖；
• 当购买额不超过给定值𝑢_𝑖时,交易费按购买𝑢_𝑖计算；
• 同期银行存款利率是𝑟_0=5%"且无交易费无风险，n=4时相关数据如下表：

问题：给该公司设计一种投资组合方案，用给定的资金M，有选择地购买若干种资产或存银行生息，使净收益尽可能大，总体风险尽可能小。

符号规定与基本假设

• 设投资风险度𝑎，总收益𝑄，投资项目𝑠_𝑖的资金为𝑥_𝑖
• 由于投资数额M相当大，而题目设定的定额𝑢_𝑖相对M很小， 𝑝_𝑖 𝑢_𝑖更小，
• 因此假设每一笔交易额𝑥_𝑖都大于对应的定额𝑢_𝑖
• 其他符号规定与假设见参考书P6

模型的建立

决策变量：𝑥_𝑖 (𝑖=0,1,2,3,4)

目标函数：净收益尽可能大(max)、总风险尽可能小(min)

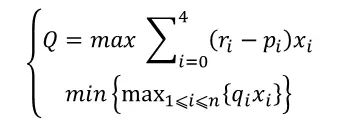
约束条件：投资总额为M、每一笔投资非负数

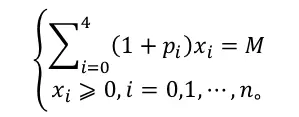
模型的简化

• 现实中，不同人所能承受的风险不同
• 设某一类投资者，能接受的最大投资风险率为定值𝑎
• 只要风险率小于等于该定值𝑎，可视为对该类投资者满足“总风险尽可能小”
• 即风险率（风险率=投资额*损失率/总资产）满足：

• 有些投资人愿意接受高风险，那么𝑎设置的大一些；反之就把𝑎设置小一些
• 总之 𝑎的大小，是我们在解题时分情况讨论的
• 基于该简化，将目标函数：𝑚𝑖𝑛{max_(1⩽𝑖⩽𝑛) {𝑞_𝑖 𝑥_𝑖 }}（总体风险尽可能小）
• 转化为了约束条件：(𝑞_𝑖 𝑥_𝑖)/𝑀⩽𝑎（总体风险小于某个常数即可）

线性规划模型

• 决策变量：" 𝑥_𝑖 (𝑖=0,1,2,3,4)，第𝑖种资产的投资额
• 目标函数和约束条件：

• 注意，除了𝑥_𝑖（5个变量），其他都是常数
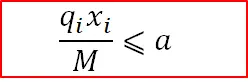
• 显然，所有变量都是线性的，因此这是一个单目标线性规划模型

其他思路

• 本题也可以不简化模型，直接建立多目标规划模型求解；
• 本题简化模型不仅仅有固定风险、极大化收益这一种方法，也可固定收益、极小化风险；也可分别赋予风险和收益相应的权重、权衡二者做出取舍；
• 总之，数学建模题目没有标准答案，各种模型只要解释合理即可。

MATLAB求解

• Matlab本身有自带函数，只需要调用就能求解问题，不需要自己写代码；
• 求解线性规划的linprog函数：[𝑥, fval ]= linprog (𝑓,𝐴,𝑏,𝐴𝑒𝑞, beq ,𝑙𝑏,𝑢𝑏)；
• Matlab中的变量，一般以矩阵的形式运算；
• 等号左边的x返回最优解的变量取值，fval返回目标函数的最优值。

注意：想用matlab自带函数求解，需要把模型化为matlab标准型

标准型：目标函数是求最小值、约束条件小于等于号或等号。

但例如本题，我们求的是最大值怎么办？约束条件有大于等于怎么办？

通过加负号解决。求y的最大值，等价于求-y的最小值；

同理，约束条件x>1，等价于-x<-1；

其中风险率a，先设定为5%；可以在求解时讨论不同的a可得到不同的结果；

a越大，代表投资者能接受更高的风险。

根据题目给的数据，可求出每一项中的常数数值（如图右侧所示）；整个模型只有5个x和y是变量。

MATLAB代码

关注公众号：数学建模BOOM，回复“线性规划”，领取代码文件；

% clc是清除命令行窗口，clear是清除存储空间的变量
% 在代码最开头写这俩是清除上一次运行的结果
clc,clear;
% a矩阵的元素是不同风险率，从0到0.05等差取值，相邻两个数相差0.001
% 因此该行代码构造出的矩阵a是包括0，0.001，0.002，……，0.05总共51个元素的行向量
% 每一个值代表一个风险率值，就可求出不同风险率下的线性规划模型的解
a = (0:0.001:0.05);
f = [-0.05,-0.27,-0.19,-0.185,-0.185];      % 目标函数的系数列向量
% A是不等式约束条件的变量系数构成的矩阵
% 由模型中不等式约束条件可以看出，模型中不等式形式的约束里，对x_0无约束，对x_1到x_4有约束且每个约束里只对一个变量有约束
% 则用zeros(4,1)先构造4行一列的全是0的矩阵，也就是对x_0无约束；
% 再构造对角矩阵diag([0.025,0.015,0.055,0.026])，数值对角线上元素为约束条件的变量系数
% 两者组合成矩阵A
% 官方资料：https://ww2.mathworks.cn/help/matlab/ref/diag.html
A = [zeros(4,1),diag([0.025,0.015,0.055,0.026])];
Aeq = [1,1.01,1.02,1.045,1.065];        % 等式约束的系数矩阵，也就是所有资产投资
beq =1;
LB = zeros(5,1);
Q = zeros(1,length(a));

% 分别求出不同风险率a情况下模型的解；从a=0开始，每次增加0.001
% lenth是求出矩阵或向量长度；a是1x51的行向量，因此length(a)是51
% 写for循环时，我们要依次用到a中每一个元素，所以要for i = 1:length(a)
% 第一次去a(1)也就是a中第一个元素值，第二次取a(2)，直到最后取到a(51),运算后循环结束
for i = 1:length(a)
    % b就是模型中约束条件的常数项矩阵
    % 本模型中每个常数项都相同，所以直接用某个常数乘以ones(4,1)
    % 代表构造4行1列的矩阵b，其中每个元素值都是常数a(i)
    b = a(i)*ones(4,1);
    % 调用linprog函数，x是对应的取值，y是最优解也就是最大的收益
    % 注意本题最开始设置总资产M=1,现实中可能是一个亿，那就把y乘以一个亿即可
    [x,y] = linprog(f,A,b,Aeq,beq,LB);
    % 利用矩阵Q存储风险率a(i)下最大的收益；for循环中i在变化，a(i)在变化，对应的Q也在变，都存下来
    % 之所以加符号，是因为本题实际是求收益最大值，
    % 而linprog函数标准型允许求最小值，在前面给目标函数等号两边加了负号转换为求最小值，、
    % 所以现在求解的结果再加符号，负负得正，就是所需求的最大值了
    Q(i) = -y;
end
plot(a,Q,'*r')      % 以风险率为横轴，收益为纵轴，绘制不同风险率下的最优收益
xlabel('风险率');        % x和y轴分别附上标签
ylabel('最大收益');

结果分析

求解图像：

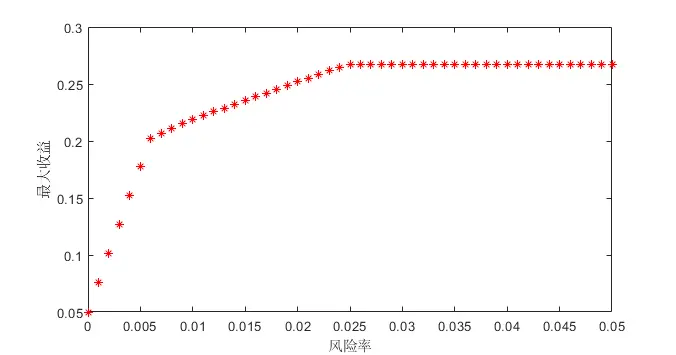
从结果可见：

• 在风险率不超过2.5%时，风险越大，收益也大。
• 在a = 0.006附近有一个转折点，在这一点左边，风险增加很少时，利润增长很快，在这一点右边，风险增加很大时，利润增长很缓慢。
• 所以对于风险和收益没有特殊偏好，或追求较低风险率的投资者来说，应该选择曲线的转折点作为最优投资组合，大约是a =0.6% ,Q =20% 。
• 该点所对应的投资方案为：风险度a=0.6%,收益Q=0.2019, x_0= 0, x_1=0.24,，x_2=0.4，x_3= 0.1091 , x_4=0.2212。
• 在a = 0.025处也有一个转折点，该点左边收益随着风险率增加而增加，该点右边则收益不变。说明整体风险率高于2.5%后没有为追求高收益而继续增大风险的必要了。

注意，本题中总投资额设置的M=1，假如现实中是一个亿，那么把代码求的收益Q乘以一个亿就是最终结果了。