MATLAB信号分析：傅里叶级数谐波分析

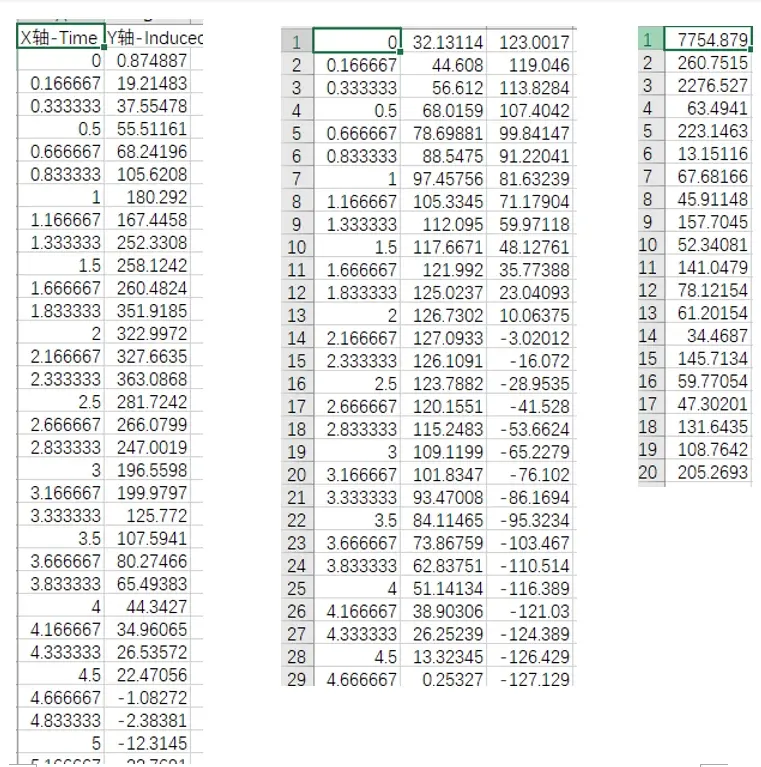
MATLAB辅导~傅里叶级数谐波波形分析需求说明如下所示：

1、根据已给的数据生成待分解的波形，然后将波形分解成不同阶次的谐波，待分解的波形和分解后的不同阶次谐波波形显示在一张图中。

2、提取不同阶次谐波的幅值，然后将不同阶次谐波幅值占基波幅值的百分比绘制成柱状图。

3、将谐波阶次设置成变量，后续根据需要就可以分解成不同阶次的谐波了。

4、将代码做成模板，之后导入不同的数据就可以一键分解不同阶次的波形和统计不同阶次谐波幅值占基波幅值的百分比。

5、将生成的不同阶次的谐波图形的数据导出，后续可以根据导出的不同阶次谐波的数据在第三方软件中重新绘图。同时，不同阶次谐波的幅值数据也需要导出。

#MATLAB仿真实验分析

#全国院校信号与系统考研辅导

#MATLAB信号与系统仿真分析

傅里叶级数仿真实验分析

傅里叶级数仿真实验是一种重要的数学和工程实验，它基于傅里叶级数理论，通过计算和分析信号的频谱成分，使我们能够理解和模拟各种周期性信号和波形。本文将详细介绍傅里叶级数仿真实验的原理和实验分析过程。

实验分析过程：

1----信号生成： 首先，我们需要生成一个周期性信号。这可以是一个正弦波、方波、三角波等。选择不同类型的信号将有助于理解傅里叶级数的应用范围。

2----采样与离散化： 对信号进行采样，将连续信号转化为离散信号。通常，我们使用模拟信号采集卡或计算机来进行离散化。采样频率需要足够高，以避免混叠现象。

3----计算系数： 通过计算信号的傅里叶级数系数，即可以使用傅里叶级数的公式进行计算。这些系数表示了信号的频谱成分。

4----频谱分析： 分析信号的频谱，查看各个频率分量的振幅和相位。这可以使用傅里叶变换或快速傅里叶变换（FFT）来实现。这有助于了解信号的频域特性。

5----频谱合成： 使用计算得到的傅里叶系数，合成信号的频谱。通过将正弦和余弦波分量相加，可以重新构建原始信号。这是验证傅里叶级数原理的关键步骤。

6----频谱绘图： 制作频谱图，显示信号的频谱成分。频谱图通常以频率为横坐标，振幅或幅度为纵坐标。这有助于可视化频域信息。

7----谐波分析： 根据傅里叶系数，确定信号中各阶谐波的幅值和相位。这对于工程应用中的滤波、信号合成和频域分析非常有用。

8----实验应用： 最后，通过实验分析，我们可以理解傅里叶级数在信号处理、通信、音频处理、图像处理等领域的广泛应用。这也有助于解决实际问题。

傅里叶级数仿真实验是数字信号处理和通信工程中的基础实验之一。通过这个实验，学生和工程师可以更好地理解周期性信号的频谱特性和傅里叶级数的应用。这对于设计和分析各种信号处理系统非常重要，包括音频处理、通信系统和图像处理。了解傅里叶级数的原理和实验过程，可以为工程和科学领域的问题提供强大的工具和洞察力。

下面针对波形的谐波分析需求进行仿真分析：

1----根据提供的csv数据绘制波形图代码如下所示：

2----根据csv数据绘制的波形进行傅里叶变换，根据输入的阶次生成对应的阶次谐波：

3----提取不同阶次谐波的幅值，然后将不同阶次谐波幅值占基波幅值的百分比绘制成柱状图。          

4----导出谐波波形的数据

5----导出谐波波形幅值的数据