MATLAB信号处理：fft函数详解‌

1.基本功能

FFT是离散傅立叶变换的快速算法，可以将一个信号变换到频域。通过FFT变换可以对信号进行频谱分析，其对应的数学表达式如下:

在MATLAB对信号的频谱分析中，模拟信号X(t)经过采样后得到含有N个采样点的数字信号X(n)，取N点进行FFT变换后，可以得到对应数量的FFT结果。

2.函数调用

Y = fft(X,n,dim)

其中，X为输入离散信号的序列，参数n（可省略）表示采样点数量，参数dim（可省略）影响X中向量的取法，fft函数将返回快速傅里叶变换结果Y。

输入的离散信号X可取向量、矩阵、多维数组，其在MATLAB中的具体取法如下。

• 当X为向量时，fft(X)将返回该向量的傅里叶变换。
• 当X为矩阵时，fft(X)将在指定的dim维上进行傅里叶变换，其中dim=1表示按列，dim =2表示按行。省略dim的情况下，fft(X)将把x的各列视为向量，并返回每列的傅里叶变换。
• 当X为一个多维数组时，fft(X)将把大小不等于1的第一个数组维度的值视为向量，并返回每个向量的傅里叶变换。

参数n为进行FFT变换的点数，与X的信号长度关系如下。

• 当X的长度小于n时，则为 X 补上尾零以达到长度 n。
• 当X的长度大于n时，则对 X 进行截断以达到长度 n。

3.参数n对频谱分析的影响

1. 幅值：根据采样定理，fft能分辨的最高频率为采样频率的一半（即Nyquist频率），函数fft返回值Y以Nyqusit频率为轴对称的，Y的前一半与后一半是复数共轭关系。将进行FFT变换的点数取做n，FFT后得到为n个复数，每一个点就对应着一个频率点，只有在有频率分量处才能在频谱图中画出对应的线；该复数的模值不等于信号的幅值，n值越大，FFT结果的模值越大，二者间数量关系将在下一部分介绍；不同模值间的比例代表了不同频率含量的比例，与FFT数量n无关。
2. 频率分辨率：当采样个数超过FFT变换的个数时，FFT会自动切断数据，此时n值越大，频率分辨率越高，如果采样数据比较少或n取值较小，则FFT变换后不能很准确的分辨出其中的频率成分；当采样个数低于FFT变换的个数时，信号在时间域内加零，致使振幅谱中出现很多其他成分，其振幅将因此减小。添加零可增加进行FFT的数量，谱的密度增高了，但仍不能分辨其中的频率成分，还会导致振幅波动，谱的分辨率没有提高。

4.编程实现

以信号x(n)为例，通过编程可得到该信号的频谱图。完整代码见文末，此处对求频谱过程的代码进行一些说明。

% 采样点数取1200 FFT变换个数取240 信号周期取(1/50) (1/150)
window=0.2*fs;
kn=2/window*fft(s1(1:window));  % FFT模值与信号幅值关系
z=fftshift(kn);				% fftshift
am=abs(z);
phase=angle(z);

• FFT模值与信号幅值关系：

FFT幅值与信号幅值关系：假设原始信号的幅值为A，窗长取N，FFT输出的模值为Y，则除了第一个点外的点，信号幅值与FFT模值有如下对应关系：A=2/N*Y，第一个点为直流分量，它的模值就是直流分量的N倍。

原因: FFT结果除以N得到双边谱，再乘以2得到单边谱。零频在双边谱中本没有被一分为二，故只需要除N即可。

•  fftshift：

对于FFT得到的频谱，横轴显示顺序为：由0开始的由小到大的正频率、0、绝对值由大到小的负频率。故要得到正确的结果，需要以0hz为中心，将右半边的负频率平移至左半边。通过函数fftshift可以实现上述变化。

即：为得到与横坐标轴对应的频谱，需要将fft后的结果通过函数fftshift进行处理。

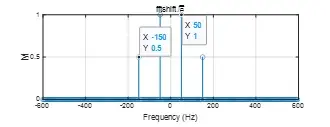
fftshift后的fft结果

5.fft相位问题

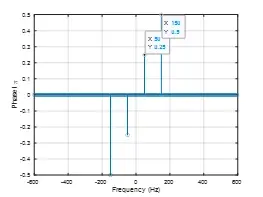
1.噪声信号过滤

为了避免输入信号s(n)经matlab求取FFT后，引入的一些幅值极小但对相位有影响的计算量，需要在相位分析前引入如下代码，实现对FFT结果的过滤。滤除前后对比图如下。

tol = 1e-6;
z(abs(z) < tol) = 0;
theta = angle(z);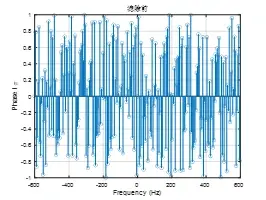

滤波前

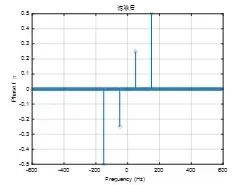
滤波后

2.初相位设置

中n的取值从1开始时，50Hz信号的初相位为,相位结果如下图：

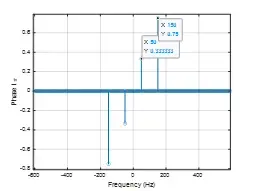
n取值从0开始时，50Hz信号的初相位才是，即：