MATLAB函数应用：解方程的多种方法

参考文献：《数学实验与数学建模》 云南大学出版社

注意事项：本专栏不是入门教程，看懂需要对matlab有一定了解。

1solve函数

1-1 符号解

代码

%本代码解决solve的用法

clc,clear

syms x a b c

jieguo=solve(a*x^2+b*x+c==0,x)

结果

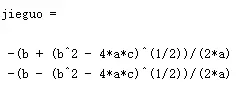
1-2数值解

求解：x^3-2*x^2==x-1

代码

%本代码解决solve的数值解

clc,clear

syms x 

s=solve(x^3-2*x^2==x-1);%获得符号解

s1=double(s);%把符号解变成双精度变量

s2=vpa(s,10);%展示某个数到10位小数

s,s1,s2

结果

1-3数值解无穷多只能给出一个的情况

解方程tan(x)-sin(x)==0

clc,clear

syms x 

jieguo=solve(tan(x)-sin(x)==0)

结果

1-4解方程组

x^2*y^2==0

x-y/2-b==0

代码

clc,clear

syms x y b

[x y]=solve(x^2*y^2==0,x-y/2-b==0);

jieguo=[x y]

结果

2 roots函数(主要用来求解多项式）

求解 x^3-2x-1==0

代码

%本代码解决roots的数值解

clc,clear

%x^3-2x-1==0

p=[1 0 -2 -1];%多项式之前的系数，从最高次幂按顺序写到常数项

jieguo=roots(p)

结果

注意有时有虚数根