MATLAB与1stOpt9.0数据拟合方法‌

看了

https://zhuanlan.zhihu.com/p/145109332?utm_source=com.yinxiang&utm_medium=social&utm_oi=46035812483072

这篇文章，想将matlab和1stOpt数据拟合做一个简单的对比。

cut-off

多项式拟合

已知数据x和y，求y=f(x)的3次多项式。其中x=[1 2 3 4 5 6 7 8 9];y=[9 7 6 3 -1 2 5 7 20];

1.1 用matlab2016的代码形式：

clear all
clc
x=[1 2 3 4 5 6 7 8 9];
y=[9 7 6 3 -1 2 5 7 20];
P=polyfit(x,y,3);
xi=0:0.2:10;
yi=polyval(P,xi);
plot(xi,yi,x,y,'r*');

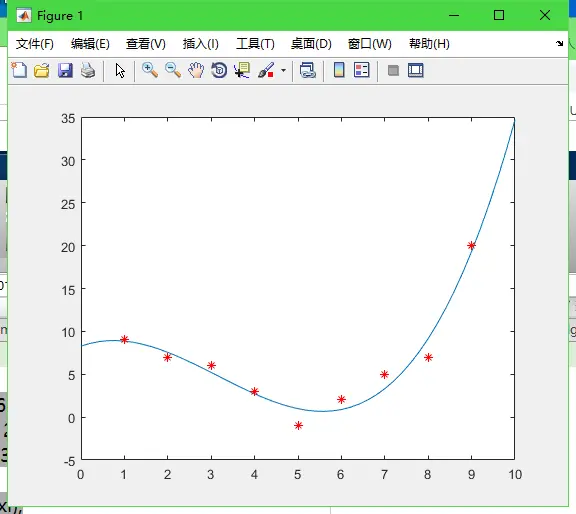
matlab拟合结果

系数结果

表达式

cut-off

1.2 也可以用工具箱：

打开工具箱

选择数据和拟合的函数形式

可以看出结果与代码形式相同。

cut-off

1.3 用1stOpt9.0

NewCodeBlock"多项式拟合";
Variable x,y;
Function  y=PolyFit(x,3); //PolyFit(x,n), n=1,2,3,...n
Data;
x=[1 2 3 4 5 6 7 8 9];
y=[9 7 6 3 -1 2 5 7 20];

模型公式: y = b0+b1*x+b2*x^2+b3*x^3
          y = 8.26984126984131+1.8536556036556*x+(-1.40295815295815)*x^2+0.148148148148148*x^3

迭代数: 0
计算用时(时:分:秒:微秒): 00:00:00:134
均方差(RMSE): 1.25561110349738
残差平方和(SSR): 14.1890331890332
相关系数(R): 0.974353666756465
相关系数之平方(R^2): 0.949365067921769
修正R平方(Adj. R^2): 0.932486757229025
确定系数(DC): 0.949365067921769
卡方系数(Chi-Square): -225.852041213259
F统计(F-Statistic): 31.2486863961482

参数	最佳估算
----------	-------------
b0	8.26984126984131
b1	1.8536556036556
b2	-1.40295815295815
b3	0.148148148148148

====== 结果输出 ======

No.	目标 Y	计算 Y
1	9	8.8686868686869
2	7	7.55050505050508
3	6	5.20418470418473
4	3	2.71861471861473
5	-1	0.982683982683962
6	2	0.885281385281327
7	5	3.3152958152957
8	7	9.16161616161598
9	20	19.313131313131

结果相同。

当然，1stOpt也可以打开二维/三维预测功能进行绘图，或获得更密集的理论数据：

2. 自定义函数进行拟合

要拟合数据

t=[0;0.4;1.2;2;2.8;3.6;4.4;5.2;6;7.2;8;9.2;10.4;11.6;12.4;13.6;14.4;15];

y=[1;0.85;0.29;-0.27;-0.53;-0.4;-0.12;0.17;0.28;0.15;-0.03;-0.15;-0.071;0.059;0.08;0.032;-0.015;-0.02];

函数：y= a*cos(k*t)*exp(w*t);

2.1 matlab 代码形式求解

clear all
clc
syms t
x=[0;0.4;1.2;2;2.8;3.6;4.4;5.2;6;7.2;8;9.2;10.4;11.6;12.4;13.6;14.4;15];
y=[1;0.85;0.29;-0.27;-0.53;-0.4;-0.12;0.17;0.28;0.15;-0.03;-0.15;-0.071;0.059;0.08;0.032;-0.015;-0.02];
f=fittype('a*cos(k*t)*exp(w*t)','independent','t','coefficients',{'a','k','w'});
cfun=fit(x,y,f)
xi=0:0.2:20;
yi=cfun(xi);
plot(x,y,'r*',xi,yi,'b-');

注释：fittype是自定义拟合函数，cfun=fit(x,y,f)拟合数据x、y，x、y必须为列向量。

结果：

cfun =

     General model:
     cfun(t) = a*cos(k*t)*exp(w*t)
     Coefficients (with 95% confidence bounds):
       a =      0.9987  (0.9836, 1.014)
       k =       1.001  (0.9958, 1.006)
       w =     -0.2067  (-0.2131, -0.2002)

经过几次尝试，发现结果还不唯一。有时效果特别差。

2.2 1stOpt拟合参数

NewCodeBlock"拟合公式参数";
 Parameter a,k,w;
 Variable  t,y;
 Function y= a*cos(k*t)*exp(w*t);
Data;
0.000	1.000
0.400	0.850
1.200	0.290
2.000	-0.270
2.800	-0.530
3.600	-0.400
4.400	-0.120
5.200	0.170
6.000	0.280
7.200	0.150
8.000	-0.030
9.200	-0.150
10.400	-0.071
11.600	0.059
12.400	0.080
13.600	0.032
14.400	-0.015
15.000	-0.020

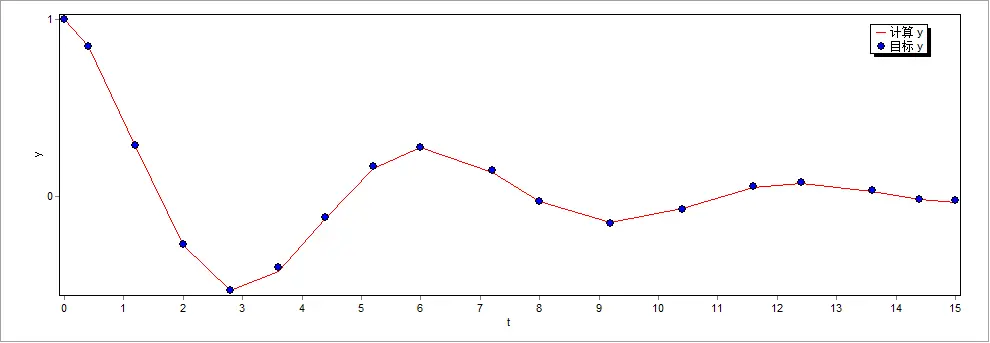
拟合公式参数

模型公式: y = a*cos(k*t)*exp(w*t)
          y = 0.99833195723151*cos(5046434.31499038*t)*exp((-0.212588170184326)*t)

迭代数: 45
计算用时(时:分:秒:微秒): 00:00:03:686
优化算法: 通用全局优化算法(UGO1)
计算结束原因: 达到收敛判断标准
均方差(RMSE): 0.0087032361372459
残差平方和(SSR): 0.00136343374669193
相关系数(R): 0.999799201134065
相关系数之平方(R^2): 0.999598442588314
修正R平方(Adj. R^2): 0.99954490160009
确定系数(DC): 0.999434250113978
卡方系数(Chi-Square): -0.00358611426503304
F统计(F-Statistic): 13315.4258002494

参数	最佳估算
----------	-------------
a	0.99833195723151
k	5046434.31499038
w	-0.212588170184326

====== 结果输出 ======

No.	实测值 y	计算值 y
1	1	0.998735313968665
2	0.85	0.846781242896686
3	0.29	0.28160034466071
4	-0.27	-0.276044071622613
5	-0.53	-0.528100607325903
6	-0.4	-0.424924154345521
7	-0.12	-0.122064052342431
8	0.17	0.161235755927997
9	0.28	0.277985358364678
10	0.15	0.136012066468729
11	-0.03	-0.0292367472541898
12	-0.15	-0.145732090357825
13	-0.071	-0.0643755508932493
14	0.059	0.0524466645385517
15	0.08	0.0760975383466458
16	0.032	0.0300940480346196
17	-0.015	-0.0138991650491467
18	-0.02	-0.0345970393063411

发现结果却是不唯一。因为cos为周期函数，所以k肯定有无数个解。

这样设置好重新计算：

拟合公式参数

重复计算最佳目标函数 (RMSE): 0.00870323607442166
重复计算求得最佳目标函数次数: 5
重复计算最差目标函数 (RMSE): 0.00870323616753541
重复计算平均目标函数 (RMSE): 0.00870323614665337
重复计算总用时: 0:00:21
优化算法: 通用全局优化算法(UGO1)
计算结束原因: 达到最大迭代数
重复最佳目标函数: 0.00870323615767501
计算用时(时:分:秒:微秒): 00:00:06:775
均方差(RMSE): 0.00870323607442166
残差平方和(SSR): 0.00136343372700806
相关系数(R): 0.999799200117992
相关系数之平方(R^2): 0.999598440556577
修正R平方(Adj. R^2): 0.999544899297454
确定系数(DC): 0.999434250122146
卡方系数(Chi-Square): -0.00358605567947675
F统计(F-Statistic): 13315.4372873641

参数	最佳估算
----------	-------------
a	0.998736079133547
k	-20076126.9403423
w	-0.206649662763963

====== 结果输出 ======

No.	实测值 y	计算值 y
1	1	0.998736079133547
2	0.85	0.846781789212204
3	0.29	0.281600383286028
4	-0.27	-0.276044263783676
5	-0.53	-0.528100683010441
6	-0.4	-0.424924004623399
7	-0.12	-0.122063833131001
8	0.17	0.161235822243856
9	0.28	0.277985188437027
10	0.15	0.136011782819056
11	-0.03	-0.0292368648986385
12	-0.15	-0.145731885436085
13	-0.071	-0.0643753232681585
14	0.059	0.052446636686817
15	0.08	0.0760973670826918
16	0.032	0.0300938916873106
17	-0.015	-0.0138991968148142
18	-0.02	-0.0345969756770301

重复运算结果(删除相同解):
1: 0.998736079133547,-20076126.9403423,-0.206649662763963; 目标函数(RMSE) = 0.00870323607442166
2: 1.15980852185743,2293667.87921584,-0.0830171689440298; 目标函数(RMSE) = 0.00870323615767501
3: 0.98228320188467,2347996.71390523,-0.217101355867249; 目标函数(RMSE) = 0.00870323616323874
4: 1.15151791550002,369042.684933169,-0.125108236529382; 目标函数(RMSE) = 0.00870323616753541
5: 0.971521416983661,165028.996538282,-0.238182920919577; 目标函数(RMSE) = 0.00870323617039605
6: 1.15151791550002,369042.684933169,-0.125108236529382; 目标函数 = 0.00136343375618213
7: 0.998735516981182,369043.889954777,-0.206649383366687; 目标函数 = 0.00136343375618213
8: 0.99873529337139,347586.812130734,-0.206649270133872; 目标函数 = 0.00136343375650608
9: 0.998735429842166,220258.06188072,-0.206649218529596; 目标函数 = 0.00136343375669592
10: 0.999614195002491,26358.9664498734,-0.208455375905937; 目标函数 = 0.00136343375743928
11: 0.99873543438024,26358.9633011076,-0.20664932022985; 目标函数 = 0.00136343375743928
12: 0.99873543438017,-1.00093750624155,-0.206649320229851; 目标函数 = 0.00136343375754432
13: 0.98228320188467,2347996.71390523,-0.217101355867249; 目标函数 = 0.00136343374932205
14: 0.998735156155269,2347995.93430362,-0.206649144729876; 目标函数 = 0.00136343375234956
15: 0.998735621575879,811191.640020977,-0.20664927094204; 目标函数 = 0.00136343375483592
16: 1.12230939886153,375200.382456683,-0.136671209915891; 目标函数 = 0.00136343375653866
17: 0.998735180250007,375201.411555722,-0.206649330320107; 目标函数 = 0.00136343375653867
18: 0.998735749551226,281236.375286843,-0.206649470636267; 目标函数 = 0.0013634337566816
19: 0.978632434066238,220413.242084218,-0.221367523731561; 目标函数 = 0.00136343375702846
20: 0.998735422367117,220413.139638409,-0.206649288552488; 目标函数 = 0.00136343375702847
21: 0.996514039507448,105998.356660907,-0.214888452664227; 目标函数 = 0.00136343375717994
22: 0.99873568926582,105998.337069682,-0.20664939799825; 目标函数 = 0.00136343375727054
23: 0.998974390418251,70592.5998850053,-0.212775195252806; 目标函数 = 0.00136343375727792
24: 0.998735576909018,70592.5878636887,-0.206649339232179; 目标函数 = 0.00136343375727792
25: 0.998735359227146,-67859.4022549964,-0.206649317966505; 目标函数 = 0.00136343375733358
26: 0.998735481197726,43258.729902431,-0.206649317966505; 目标函数 = 0.0013634337575177
27: 0.998735426447321,-189.496496723021,-0.20664932185414; 目标函数 = 0.00136343375754405
28: 0.998735435754625,93.2468421012542,-0.20664931938688; 目标函数 = 0.00136343375754419
29: 0.998735433237852,61.8309155632644,-0.2066493201585; 目标函数 = 0.00136343375754429
30: 0.998735434380216,1.00093750624155,-0.206649320229847; 目标函数 = 0.00136343375754432
31: 0.971521416983661,165028.996538282,-0.238182920919577; 目标函数 = 0.0013634337570318
32: 0.998735574350008,165028.863030548,-0.206649359889561; 目标函数 = 0.00136343375707842
33: 0.998735472571832,91421.3471569728,-0.20664933614138; 目标函数 = 0.00136343375725871
34: 0.998735440971241,-95.2487171850403,-0.206649325367026; 目标函数 = 0.00136343375754403
35: 0.998735438044114,30.4149890295845,-0.206649321102916; 目标函数 = 0.00136343375754428
36: 0.998736079133547,-20076126.9403423,-0.206649662763963; 目标函数 = 0.00136343372700806
37: 1.01617254477805,-7806075.79599842,-0.196570846099928; 目标函数 = 0.00136343373154521
38: 0.998735156913937,-7806073.34694413,-0.206649644615355; 目标函数 = 0.00136343373154525
39: 1.11115337261464,-4747776.45724106,-0.13948427714038; 目标函数 = 0.0013634337400753
40: 0.998735088330856,-4747764.31460171,-0.206649288966944; 目标函数 = 0.00136343374007531
41: 1.01736888928808,-1952061.77194194,-0.189499998614917; 目标函数 = 0.00136343374927731
42: 0.998735642013637,-1952061.01217205,-0.206649387173815; 目标函数 = 0.00136343375060406
43: 0.998735355961833,-1534669.01221612,-0.206649337949481; 目标函数 = 0.00136343375309647
44: 0.998735817683769,-1091987.19139866,-0.20664946682597; 目标函数 = 0.00136343375437449
45: 0.998735275678054,-658541.652983054,-0.206649365932585; 目标函数 = 0.00136343375555999
46: 1.28664628194045,283842.052110602,0.0425994278413256; 目标函数 = 0.00136343375630364
47: 0.998735435502374,283843.897189358,-0.206649320851223; 目标函数 = 0.00136343375630364
48: 0.977988453613241,-146051.537604309,-0.234319085368998; 目标函数 = 0.00136343375723216
49: 0.998735339689298,-146051.641527868,-0.206649332831268; 目标函数 = 0.00136343375734037
50: 1.00136793213992,-82153.6615008555,-0.201176077309531; 目标函数 = 0.00136343375736986
51: 0.998735347522712,-82153.6488288996,-0.206649369708141; 目标函数 = 0.00136343375737383
52: 0.998735437418344,63.832790609982,-0.206649322686235; 目标函数 = 0.00136343375754408
53: 0.998735433148613,-93.2468421010316,-0.206649319930943; 目标函数 = 0.00136343375754416
54: 0.998735435159131,32.41686405037,-0.206649320855254; 目标函数 = 0.00136343375754427
55: 0.998735435089812,-30.4149890289587,-0.206649320408333; 目标函数 = 0.00136343375754427
56: 1.15980852185743,2293667.87921584,-0.0830171689440298; 目标函数 = 0.00136343375305729
57: 0.998735422579374,2293675.79544838,-0.206649311060799; 目标函数 = 0.00136343375305729
58: 0.998734783864033,1253808.62711017,-0.20664917411396; 目标函数 = 0.00136343375638495
59: 0.99884876091719,72100.5644763504,-0.212748368633829; 目标函数 = 0.00136343375729015
60: 0.998735467811686,72100.5523373824,-0.206649283699807; 目标函数 = 0.00136343375729016
61: 0.998735434383649,-32.4168640417783,-0.206649321085354; 目标函数 = 0.00136343375754423

重复运算结果(全部解):
1: 0.998736079133547,-20076126.9403423,-0.206649662763963; 目标函数(RMSE) = 0.00870323607442166
2: 1.15980852185743,2293667.87921584,-0.0830171689440298; 目标函数(RMSE) = 0.00870323615767501
3: 0.98228320188467,2347996.71390523,-0.217101355867249; 目标函数(RMSE) = 0.00870323616323874
4: 1.15151791550002,369042.684933169,-0.125108236529382; 目标函数(RMSE) = 0.00870323616753541
5: 0.971521416983661,165028.996538282,-0.238182920919577; 目标函数(RMSE) = 0.00870323617039605

返回上级列表

请

联系我们

，获取更多内容

< 上一篇: 带时滞传染病模型分析：基于MATLAB的动力学模型学习笔记‌

下一篇: MATLAB手写数字识别实战：MNIST数据集‌ >