Matlab差分法初步探索电磁场问题‌

今天刚到学校就遇到了在努力复习准备补考电磁场的室友

他也问了我好几道相关的题目，我也刚好想到最近在学习的Matlab在解决电磁场数值分析的问题上其实是个大杀器

在电磁场的实际应用中，会大量出现复杂的边界数值分析问题，但是这些问题人为处理起来十分棘手和麻烦，但是使用计算机进行分析和处理却具有很大的可行性。随着最近几十年来计算机的更新换代，算力得到了极大的补充和增强，也使得计算机在处理复杂问题时具有了不可忽视的优势。

在电磁场数值计算分析中，通过计算机将连续的电磁场问题转化成离散系统，并对其进行求求解，通过场域内的离散化的模型的数值解近似出连续场的真实解，目前常用的方法主要是有限差分法、有限元法、矩量法和边界元法。这篇文章中主要讨论有限差分法。

有限差分法吧连续空间离散化，把导数以差分近似，从而把偏微分方程转化为差分方程（代数方程），再采用适当的算法求解，得到原问题的近似解。

空间离散化的越细，解的误差越小，但差分方程组的未知量也越多，相应的计算负担也越大。

这是当初上课拍下的一道例题

Matlab仿真的结果

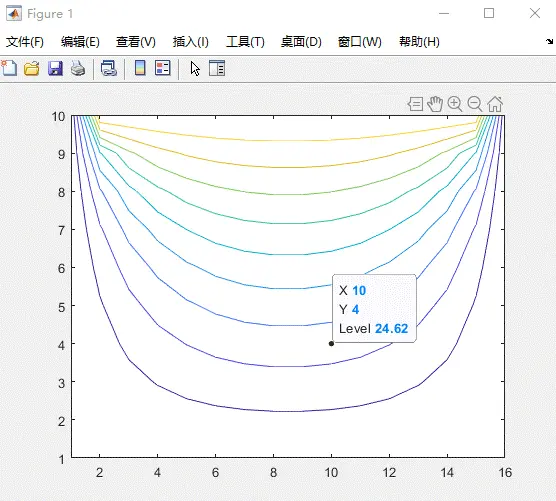
总结：

在计算机技术快速发展的今天，依托于计算机来通过离散的差分方程组的解近似得到偏微分方程的近似解也将成为一种趋势。在用计算机解决电磁场问题时，关键在于对实际问题的数学模型的准确建立，这直接关系到程序的建立思路和执行效率。在做完题目之后我又用简单迭代法和超松弛迭代法进行了计算，虽然得到了近似的结果，但是观察了迭代次数后发现高斯-赛德尔迭代法一共迭代了222次，而超松弛迭代法只需要38次，大大提高了收敛速度。

下面是具体的代码，仅供参考