前段时间完成了一个关于三边定位算法的课程设计。但是发现网上关于三边定位MATLAB的程序代码挺少的,所以想整理一下,供最初初初初级的初学者简单借鉴一下(拿来直接用)。
三边定位中涉及到是否要将测距误差纳入考虑范围中,因此要考虑到不存在误差时的理想情况(三个圆交到一个点)和存在误差时的实际情况(三个圆无法交到一个点)。因此一共分为两章进行讨论。
PS:此文章仅供菜鸟做课题临时使用,程序有很大的漏洞,专业做课题的请不要看了,会浪费您的时间。同时欢迎有人能解决我第二章程序的疑问。
ps:建议看完理想情况再看存在误差的实际情况,不要跳要不看不懂了。
一、理想情况下的三边定位
三边定位(trilateration)法:分别以三个已知点位(例如雷达、测距仪)为圆心,待测点到已致点距离为半径作圆。三个圆相交点O为未知点位置。如下图1所示。

图1 三边定位
设未知点O坐标为(x0,y0),三个测量点为圆心坐标分别为A(x1,y1)、B(x2,y2)、C(x3,y3),三个已知点到未知点O距离分别为d1、d2、d3。那么三边定位公式如下图2。
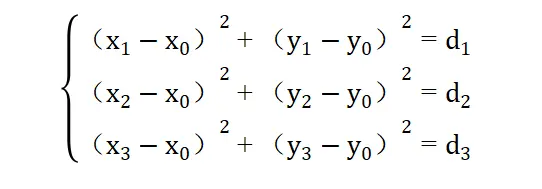
图2 三边定位原理公式(不好意思b站一加公式就卡,只能截图了)
程序如下:
注意下边的程序是一个函数。需要新建一个函数源文件,然后再用这个程序!!!
function [locx,locy] = triposition(x1,y1,d1,x2,y2,d2,x3,y3,d3)
% 三点定位法 %
%输入:
% 1.参考节点A(x1,y1),B(x2,y2),C(x3,y3)
% 2.定位节点O(locx,locy)到这三点的距离分别为d1,d2,d3
% (locx,locy)为计算的定位节点O点的位置坐标
syms x y %f符号变量
%--------------求解方程组------------------------------------
f1=(x1-x)^2+(y1-y)^2-d1^2;
f2=(x2-x)^2+(y2-y)^2-d2^2;
f3=(x3-x)^2+(y3-y)^2-d3^2;
% 解关于x,y的符号方程组,得到解的符号表示,并存入xx,yy
[xx,yy] = solve(f1,f2,f3,x,y);
px = eval(xx); %解的数值px(1),px(2)
py = eval(yy); %解的数值py(1),py(2)
locx = px;
locy = py;测试:
寻找上边绿色的开始箭头“运行” 或者 “下边命令行窗口”,输入下边的内容
输入:[locx,locy] = triposition(0, 0, 1, 2, 0, 1, 1, 1, 1)
输出:locx = 1;
locy = 0;
二、实际情况下的三边定位
由于测距误差的存在,因此以测量距离为半径的三个圆无法相交于一点,因此会出现如下图3所示情况。
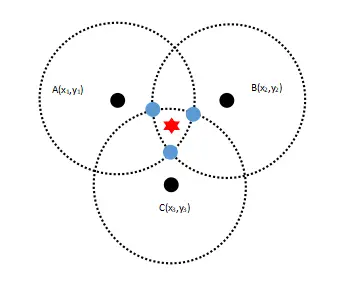
图3 存在测距误差的三边定位实际情况
直接上程序,我已经标明了改动部分,但这个程序是参考了别人的程序,恰巧发现能用,但为什么这么写-存在误差的时候能用我就不知道。仅供菜鸟快速完成课设使用,做专业课题的忽略掉我,谢谢。
(22年4月30日修改为什么能用,感谢评论区Ertist解析)
下边使用高中方法解释一下,谁有更好解释可以再说一下。
可以理解为:在理想的状态下,我两个方程f4、f5的解都是在x轴上,那么很成功我们能有一个公共的解。相对应的,在实际情况下,两个方程f4、f5的交点不在x轴了,但我仍然还是有一个交点。
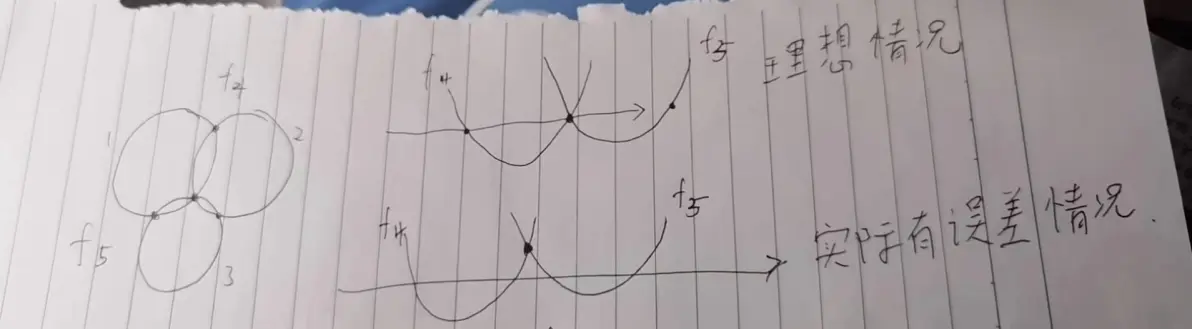
手工画,大师造
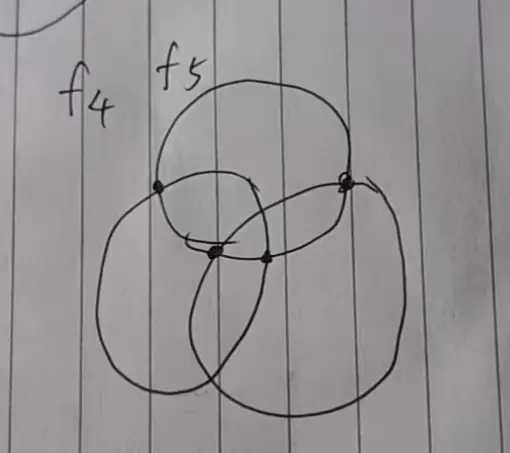
手工画,真难看
function [locx,locy] = triposition(x1,y1,d1,x2,y2,d2,x3,y3,d3)
% 三点定位法 %
%输入:
% 1.参考节点A(x1,y1),B(x2,y2),C(x3,y3)
% 2.定位节点O(locx,locy)到这三点的距离分别为d1,d2,d3
% (locx,locy)为计算的定位节点O点的位置坐标
syms x y %f符号变量
%--------------求解方程组------------------------------------
%-------理想情况到实际情况的变动部分-----------------------
f4=(x1-x)^2+(y1-y)^2-(x3-x)^2-(y3-y)^2-d1^2+d3^2;
f5=(x2-x)^2+(y2-y)^2-(x3-x)^2-(y3-y)^2-d2^2+d3^2;
% 解关于x,y的符号方程组,得到解的符号表示,并存入xx,yy
[xx,yy] = solve(f4,f5,x,y);
%--------------变动部分截止-------------------------------
px = eval(xx); %解的数值px(1),px(2)
py = eval(yy); %解的数值py(1),py(2)
locx = px;
locy = py;当然%---理想情况到实际情况的变动部分--按照参考 CSDN博主「知行流浪」 进行稍微调整得到的如下,也是可以的
%-------理想情况到实际情况的变动部分-----------------------
f4 = 2*x*(x1-x3)+x3^2-x1^2+2*y*(y1-y3)+y3^2-y1^2-d3^2+d1^2;
f5 = 2*x*(x2-x3)+x3^2-x2^2+2*y*(y2-y3)+y3^2-y2^2-d3^2+d2^2;
% 解关于x,y的符号方程组,得到解的符号表示,并存入xx,yy
[xx,yy] = solve(f4,f5,x,y);
%--------------变动部分截止-------------------------------测试:(实际情况章节内的两个程序,分别测试有、无误差的两种情况,测试输出结果相同)
①有误差时(无法交于一点):
输入:[locx,locy] = triposition(0, 0, 1.2, 2, 0, 1.3, 1, 1, 1.1)
输出:locx = 0.9375;
locy = 0.1775;
②没有误差(能够交于一点):
输入:[locx,locy] = triposition(0, 0, 1, 2, 0, 1, 1, 1, 1)
输出:locx = 1;
locy = 0;
三、拓展
当然等之后深入一点你可以考虑质心定位算法,如图4。
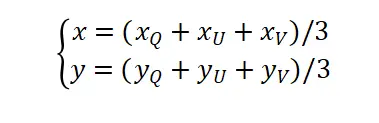
图4 质心定位算法
如下图5所示,在未知点周围会出现Q、U、V三个交点那么运用质心定位算法是不是可以大致算出未知点/待测点(红星星)位置呢。
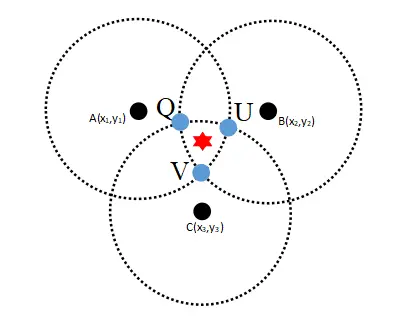
图5 在未知点周围会出现Q、U、V三个交点
这里只是提供一个思路因为是21年做的一个内容所以懒得再深究了,看到这里你已经知道最基本的三边定位怎么做了,所以后边的内容请大家自行学习,如果有做法,可以分享到评论区,给后人参考(可以是方法或者是网址都可以),我看22年4月底开始大家做课题的开始多了,互相分享吧加油!!!
深层次探究还请大家自行学习,仅供菜鸟入门,谢谢。
参考:
CSDN博主「知行流浪」https://blog.csdn.net/zengxiantao1994/article/details/70212895
如有侵权,请联系我我会删除。