Fluent PBM：成核与颗粒生长引起的相间传质

1.设置

在涉及颗粒产生、溶解或生长（如结晶）的应用中，由于这些现象，颗粒相的总体积分数方程将具有源项。由于质量的增加，颗粒相的动量方程也会有源项。在Ansys Fluent中，可以使用UDF宏DEFINE_HET_RXN_RATE（参见异相反应部分该宏介绍）或使用相位交互选项卡指定质量源项。

Fluent相间作用|多相反应

b占余文乐 · 7557阅读

例如，在结晶过程中，粒子是通过成核（n0）产生的，也可以指定生长速率（G）。所有尺寸颗粒的传质速率（in kg/m³-s）为

$\begin{aligned} \dot{m} & =3 \rho K_v \int_0^{\infty} L^2 G n(L) d L \\ & =\frac{1}{2} \rho K_a \int_0^{\infty} L^2 G n(L) d L \end{aligned}$

对于离散方法，由于生长导致的传质速率可以写成：

$\begin{aligned} \dot{m} & =\rho \int_0^{\infty} G_v n(L) d L \\ & =\rho \int_0^{\infty} G_v n(V) d V \\ & =\rho \sum_i G_{V, i} N_i \end{aligned}$

如果总传质过程中包含成核速率，则传质过程为：

$\dot{m}=\rho V_0 \dot{n}_0+\sum_i \rho G_{V, i} N_i$

重点:对于离散方法，总体平衡方程的源必须和为总传质速率。要访问源代码，可以使用宏C_PB_DISCI_PS (cell, thread, i)

对于SMM，只有一个与尺寸无关的增长率是可用的。因此，传质速率可以写成：

$\dot{m}=\frac{1}{2} \rho K_a G m_2$

对于QMOM，传质速率可以写成

$\dot{m}=\frac{1}{2} \rho K_a \sum_i L_i^2 w_i G\left(L_i\right)$

对于SMM和QMOM，由于成核的传质可以忽略不计。

重要提示:注意，对于结晶，初级相有多个组分;至少，有溶质和溶剂。要定义多组分多相系统，您需要在激活多相模型后，在物种模型对话框中激活主要阶段的物种传输。建立物种迁移问题的其余步骤与建立单一阶段的物种迁移问题相同。多相反应定义为: liquid(solvent)j→crystal(solute)

当激活种群平衡模型时，可以自动完成非反应物质（如沸腾）和异相反应（如结晶）相之间的质量传递，而不是挂钩 UDF。

由于非反应物质的成核和生长现象，对于主和次相之间的简单单向传质，配置以下设置:

在Multiphase Model对话框中，打开Phase Interaction > Heat, Mass, Reactions > Mass
指定案例Number of Mass Transfer Mechanisms
对于每个机制，在 From Phase 下指定源材料的阶段，在 To Phase 下指定目标材料阶段的阶段。
从机制下拉列表中，选择一种机制：

none 如果您不想在相之间进行任何传质
constant-rate 对于固定的、用户指定的速率
user-defined 如果你挂载了一个描述传质机制的 UDF
population-balance 用于质量转移的自动化方法，不涉及 UDF。由种群平衡核计算的成核和增长率用于传质。

注：对于非均匀离散种群平衡模型，如果存在一个以上的次级相，则可以选择种群平衡作为溶剂相（例如结晶）和非均匀离散群体平衡模型下定义的每个溶质相之间的传质机制。

5.点击apply

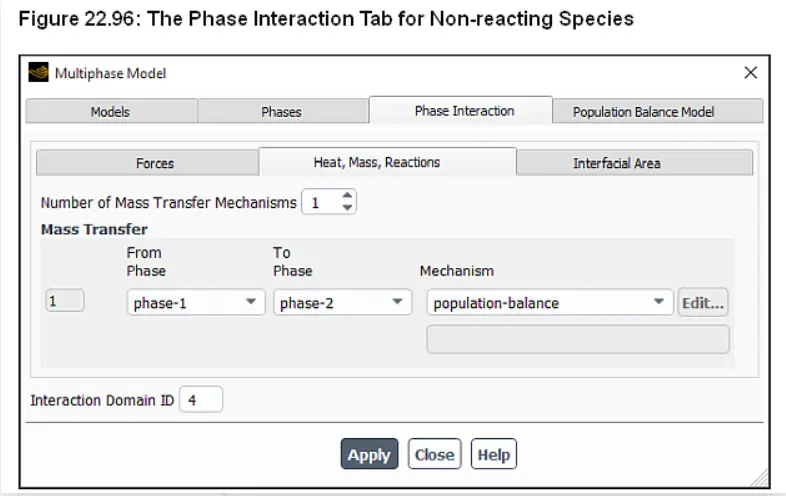
对于异相反应，请配置以下设置：

对于主相，激活Species Transport模型
在Multiphase Model对话框中，打开Phase Interaction > Heat, Mass, Reactions > Reactions
在“Reactions”选项卡下，指定反应物和产物的化学计量。
选择“population-balance”作为 Reaction Rate Function.
点击OK保存

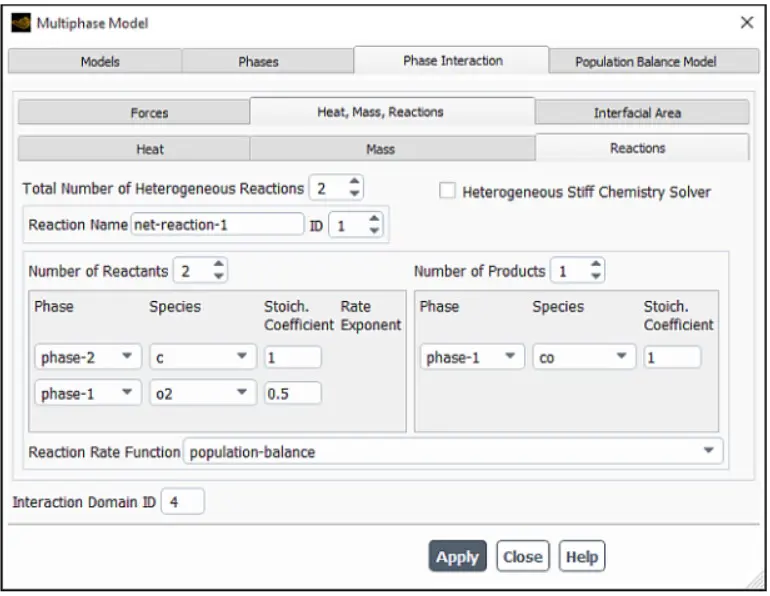
这种方法或使用DEFINE_HET_RXN_RATE宏中描述的UDF都会产生相同的结果。

对于涉及成核和生长的非均匀离散平衡模型，您可以选择 population-balance 作为已设置的每个非均相反应的反应速率函数。

2.理论

2.1 种群平衡方程（PBE）

假设 Φ是粒子体积，数密度函数的输运方程为：

$\begin{aligned} & \frac{\partial}{\partial t}[n(V, t)]+\nabla \cdot[\vec{u} n(V, t)]+\underbrace{\nabla_v \cdot\left[G_v n(V, t)\right]}_{\text {Growth term }}=\underbrace{\frac{1}{2} \int_0^V a\left(V-V^{\prime}, V^{\prime}\right) n\left(V-V^{\prime}, t\right) n\left(V^{\prime} t\right) d V^{\prime}}_{\text {Birth due to Aggregation }} \\ & \underbrace{-\int_0^{\infty} a\left(V, V^{\prime}\right) n(V, t) n\left(V^{\prime}, t\right) d V^{\prime}}_{\text {Death due to Aggregation }} \\ & \underbrace{+\int_{\Omega_r} p g\left(V^{\prime}\right) \beta\left(V \mid V^{\prime}\right) n\left(V^{\prime} t\right) d V^{\prime}}_{\text {Birth due to Breakgge }} \\ & -\underbrace{g(V) n(V, t)}_{\text {Death due to Breakage }} \\ & \end{aligned}$