距离上一次更新专栏文章已经快两年了,第一次在B站上更新专栏文章还是在2020年9月份,当时研二刚开学,由于疫情在家里面呆了8个月,虽然是线上听课,但是空闲时间还是比较多的,不想浪费时间,就自学了Abaqus的相关内容。9月份开学后,要进入相关课题研究,主要研究多体动力学与振动疲劳,和有限元相关不大,但是为了避免忘记曾经学过的知识,就通过文章的形式分享到B站上,后来有很多人在B站上私信我,开始还有时间回复一下,后来太忙了也基本不上B站了。现在我也要毕业了,工作以后大概率不会用到这些东西了,所以利用毕业之前这一段真空期,总结一下曾经学过的知识。
之前曾经做过轴承类的仿真,但是保持架与滚珠之间的接触一直定义不好,当时利用连接器Connector中的Link连接每个滚珠,取代保持架,但是仍然没有收敛,后来将保持架与滚珠之间的法向接触属性定义为“软接触”,效果比较好。本案例一共使用了静力学与隐式动力学2种计算方法,建模过程的重复部分不再赘述。
静力学(Stastic)分析:
Part(零件):
本例的轴承由外圈、内圈、保持架与滚珠组成。

Property(属性):
常见的钢材,只定义线弹属性,未考虑塑性变形。

Assembly(装配):
轴承装配体由1个内圈,1个外圈,11个保持架,11个滚珠组成。

Step(分析步):
共建立2个分析步,第一个分析步定义Y轴负方向的力,主要为了建立轴承内部零件的接触关系。第二个分析步定义轴承内圈的角速度,带动滚珠转动。为了增强收敛效果,初始分析步长、最小分析步长与最大分析步长尽量定义的小一点。

Interaction(接触):
模型中每个滚珠要定义4个接触对:滚珠与轴承外圈内侧、滚珠与轴承内圈外侧、滚珠与左侧保持架、滚珠与右侧保持架。模型中一共12个滚珠,整个模型共定义了48个接触对。为了方便定义接触对时选择主从面,将每个接触对的主面与从面定义了Surface集合。
轴承内圈的内侧定义Coupling约束(Constraint中定义),需要在圆心处定义RP(Reference Point)点。Control points选择RP点(RP1),Surface选择轴承内圈的内侧。约束类型(Coupling type)分为刚性与柔性两种,所谓柔性约束(Continuum distribution/Structural distribution),就是约束所有的转动自由度(二维问题只有U1、U2、UR3共3个自由度,因此只约束UR3自由度),类似Hypermesh中的Rbe3单元,就是将载荷平均施加在所约束的Surface面上,而刚性约束(Kinematic),就是约束所有的自由度(三维问题约束6个自由度,二维问题约束3个自由度),把所约束的Surface面定义为刚体。两种约束方式达到的仿真结果是不一样的,会在后面比较。

保持架的内侧同样定义Coupling约束,Control points选择RP点(RP2),RP1与RP2两个RP点均定义在圆心处,选则时比较困难,因此分别应定义RP1点与RP2点的Set集合,方便选择,Surface选择保持架的内侧,刚性约束。

(1)滚珠与轴承外圈内侧接触:轴承外圈内侧为主面(红色),滚珠为从面(紫色),滑移类型为有限滑移(Finite sliding),法向硬接触,切向摩擦系数为0.05。
定义接触控制(Contact controls)是因为调试了很多次都不收敛,曾经尝试在接触属性中增加阻尼,但是效果更不好了。甚至修改了软件的求解设置,增加迭代次数(Equil Iter,EI)与严重不迭代次数(Severe Discon Iter,SDI),将迭代不收敛后“折减”的次数增加至10次(默认是5次,就是迭代时出现5U后计算报错),收敛效果仍然比较差,只能完成整个仿真的25%。个人认为这个稳定系数(stabilization factor)定义的越小越容易收敛,微信公众号有篇文章专门介绍这个接触稳定系数,虽然这个系数有助于收敛,如果定义不合理将造成严重的分析误差。

(2)滚珠与轴承内圈外侧接触:轴承外圈内侧为主面(红色),滚珠为从面(紫色),滑移类型为有限滑移(Finite sliding),法向硬接触,切向摩擦系数为0.05。

(3)滚珠与左侧保持架接触:保持架为主面(红色),滚珠为从面(紫色),滑移类型为有限滑移(Finite sliding),法向为“软接触”,切向无摩擦。
法向接触属性默认为硬接触(Hard Contact),主面与从面的接触间隙为0时才建立接触关系,如果法向接触为默认属性,滚珠与保持架之间接触不好控制。如果建模有误差,主面与从面之间有接触间隙,可以定义容差范围(Specify tolerance for adjustment zone),强制让主面与从面建立接触关系。
所谓“软接触”,是指主面与从面之间仍存在一定距离时,软件便认为他们之间建立了接触关系,由于滚珠与保持架之间间隙为0.05 mm,所以其容差间隙(Clearance)应大于0.05mm,为此取0.1mm,Pressure为法向的接触力。

(4)滚珠与右侧保持架接触:保持架主面(红色),滚珠为从面(紫色),滑移类型为有限滑移(Finite sliding),法向为“软接触”,切向无摩擦。

Load(边界条件与载荷):
轴承外圈的边界条件:轴承外圈外侧约束全部自由度。

轴承内圈的力载荷:第一个分析步,在RP1点(轴承内圈定义了Coupling约束)处定义U2(Y轴)负方向100N的集中力,第二个分析步继承第一个分析步定义的集中力,力不用过大,因为没有考虑材料的塑变,只为了建立接触关系。

轴承内圈的边界条件与速度载荷:由于在U2方向定义了集中力,因此RP1点的边界条件(速度/位移,velocity/displacement)应该释放U2方向的自由度。第一个分析步约束RP1点V1方向、VR3方向的自由度,释放V2方向的自由度。第二个分析步要定义速度载荷,约束RP1点V1方向的自由度,释放V2方向的自由度,VR3方向定义角速度3.14 rad/s,本来想定义的大一点,但是收敛效果不好。

保持架的边界条件:约束RP2点U1、U2方向的自由度,释放UR3方向自由度.

Mesh(网格):
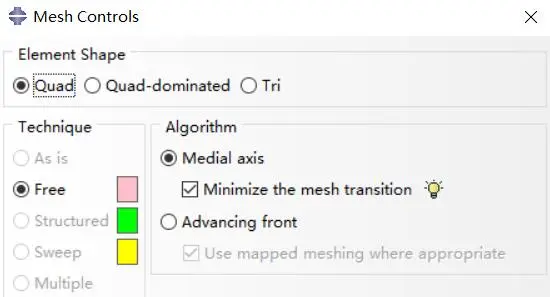
2D网格一般采用自由网格划分方法,轴承的内圈与外圈网格尺寸为0.5 mm,滚珠与保持架的网格尺寸为0.2 mm,滚珠切分出了一个圆环是为了保证滚珠接触区域全部为四边形网格。
网格属性为CPS4I(平面应力问题),非协调积分单元,静力学使用隐式算法,需要不停地迭代,还是不要用缩减积分单元或者完全积分单元。

Visualization(后处理结果):
静力学分析确实很难收敛,总共迭代了4400步才收敛。而且在滚珠滚动过程中,滚珠与保持架之间始终保持间隙,没有直接接触。轴承内圈内侧柔性约束时,有应力的变化,而刚性约束时,轴承内圈内侧完全刚化。

隐式动力学与静力学均使用隐式算法,因此其属性、接触、网格设置均与静力学分析设置相同。因为静力学分析是一种稳态的过程,时间是没有意义的,可以理解为“份数”,而隐式动力学中设置的时间是有真实意义的。
Step(分析步):
共建立两个隐式动力学分析步,时间均为0.1 s。

第一个分析步Step-1。

第二个分析步Step-2。

Load(边界条件与载荷):
边界条件与载荷的定义与静力学分析设置基本一直,但是由于动力学的时间是有真实意义的,因此集中力要定义载荷曲线。
轴承内圈的力载荷:第一个分析步0到0.1 s,在RP1点定义100 N的集中力从0线性增长至100。第二个分析步0.1 s到0.2 s,集中力保持100 N平稳不变。

轴承内圈的边界条件速度与载荷:第一个分析步0到0.1 s,RP1点约束V1与VR3方向自由度,释放V2方向的自由度。第二个分析步0.1 s到0.2 s,RP1点约束V1方向自由度,释放V2方向的自由度,VR3方向定义角速度104.72 rad/s。

Visualization(后处理结果):
从后处理云图看出,轴承滚珠与保持架之间始终保持一定间隙。

静力学与隐式动力学的仿真动画,上面两个为静力学,下面两个为隐式动力学。
