具有周期结构的血管支架有限元分析

李萍萍，张若京(同济大学航空航天与力学学院，上海 200092)摘要：用于治疗血管狭窄的血管支架是一个具有周期微结构的圆管型结构。该文分析的是管型气囊扩张式的支架，在植入血管的过程中，支架随着气囊的受压膨胀而受到内压继而发生形式为均匀膨胀的弹塑性变形。该文自行设计了一种支架，并选择适当的周期微结构即代表性单胞作为数值仿真的模型，构造了相应的周期边界条件，对上述变形过程进行了有限元分析。最后通过后处理程序得到完整支架的分析结果。结果主要包含两个方面：一是对应力和变形的预测。这对血管支架的设计以及长期服役的效果分析是至关重要的；另一个结果是给出了内压与支架直径之间的关系曲线。可为医生的植入手术提供重要参考。分析采用 ABAQUS/Explicit 分析模块。因为只分析一个代表性单胞就可以代替对整个支架结构的分析，所以可大大节约计算成本。关键词：力学；有限元；血管支架；周期结构；周期边界条件；多点约束方程

血管支架对于心脑血管疾病的治疗效果越来越受到人们重视。对于气囊扩张式的血管支架，其植入过程是，首先借助输送系统将其送达血管病变处，然后对气囊充压，通过气囊的膨胀迫使支架扩张。当支架直径达到需要的尺寸后，气囊泄压，退出血管，只留膨胀后的支架在指定位置。支架在正式生产前，必须经过大量的膨胀性能实验。因为支架尺寸微小，搭建模拟真实环境的实验台比较困难且耗资不匪。而动物实验昂贵又有不确定性。因此对血管支架扩张过程的数值模拟就成为预测支架膨胀性能的重要手段。另外，不同的设计对血管支架的柔顺性、抗压性，甚至是手术后血管再狭窄、细胞内膜增生等都有着显著的影响[1―2]。所以对血管支架的应力和变形预测十分重要。

为了方便植入，支架的原始直径一般都很小，而在膨胀后需要充分撑起狭窄的血管，且在气囊撤压后不发生回弹，因此支架的变形属于塑性大变形，涉及几何和材料非线性。另外，气囊和支架之间存在复杂的接触关系，分析时压力不能直接施加在支架上[3]，而是要通过接触关系来实现，所有这些都增加了对血管支架进行数值模拟的复杂性和难度[4―6]。本文采用有限元方法模拟了管型气囊扩张式支架的变形过程，计算出支架变形后的形状及应力分布，可为支架设计提供参考。

现有对血管支架的有限元分析大多利用了支架结构的对称性，即取沿轴向一半和沿环向四分之一的部分进行建模和分析[7―9]。相当于计算八分之一模型。而本文将支架计算模型缩减为一个更小的代表性单胞。代表性单胞尺寸远比八分之一模型小。本文计算的血管支架被划分为 18 个代表性单胞。所以，本文方法大大节约了计算成本。

1 周期边界条件

因为周期结构上任意一点都属于一个代表性单胞，所以点的位移可以分解为代表性单胞的整体位移加上局部位移。就是说，周期结构的位移场可以表示为：

因为血管支架的内表面受均布压力，所以每个代表性单胞的载荷都相同，都是均布压力。这样，除了支架的自由端附近以外，结构的变形和应力-应变分布也都具有周期性。因此，只要在一个代表性单胞上施加恰当的周期边界条件进行计算分析，最后通过后处理显示代表性单胞的组合，就可以得到整个支架模型的分析结果。

2 血管支架建模

2.1 支架、气囊的几何模型及代表性单胞的选择

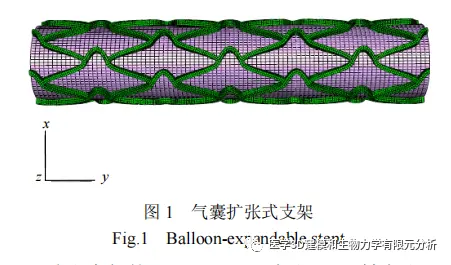
常见的气囊扩张式血管支架可以分为管状、网状等，由于网状支架容易引起血栓和细胞内膜增生，所以现在的冠脉支架多是由多个波形支撑筋通过连接筋构成的管网状结构。支撑筋的横截面近似为矩形，且通常支撑筋的厚度和宽度在 0.07mm~0.1mm 左右。利用 Pro/E 建模软件建立支架和气囊的几何模型，如图 1。这种形状的支架连接筋为弯曲曲线形状，与早期的支架，例如 Palmaz-Schatz支架，相比具有较好的弯曲性能(柔顺性)。其中波形支撑筋的中心线为正弦曲线。连接筋的中心线为半个波形的余弦曲线。

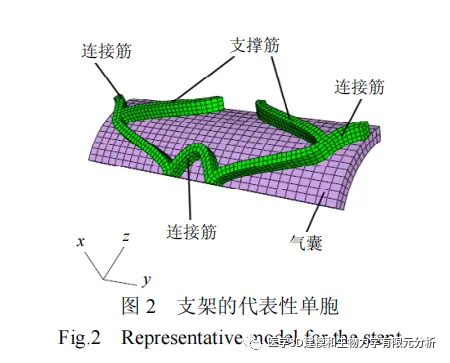
选取支架的 1/18，即沿环向取 1/6，轴向取 1/3的部分作为气囊扩张式支架的代表性单胞，见图 2。图 2 中底部为气囊，上部网状物为支架。

虽然当支架在血管内撑开时要受到来自血管的径向压力，但显然只要增加内压，就可以将其抵消，而认为支架不受外载荷。所以，本文忽略血管壁的径向压力的影响。

利用 Pro/E 建模软件建立支架和气囊的几何模型。其中波形支撑筋的中心线为正弦曲线，幅值为0.2mm。连接筋的中心线为半个波形的余弦曲线，幅值为 0.1mm。代表性单胞的长度为 2.4mm，旋转边界面之间的角度为 60°。支撑筋的厚度为 0.1mm，宽度 0.07mm。采用 Hypermesh 软件对模型进行网格划分，再使用 ABAQUS/Explicit 求解器计算。采用六面体单元对气囊和支架进行网格划分，并选择Explicit 单元库里的 8 节点六面体线性缩减积分单元(C3D8R)作为单元类型。在厚度方向上，气囊划分为两层单元，支架划分为三层。支撑筋和连接筋的交界处进行网格细化。整个计算模型的单元总数为 1656 个，节点总数为 3039 个。

2.2 代表性单胞的接触设置和载荷设置气囊和支架之间的接触关系在计算中十分重要。选择面面接触法则来模拟气囊和支架之间的接触关系，并选择 Coulomb 模型来模拟气囊和支架之间的摩擦类型。这种模型由摩擦系数来决定接触面承担的剪应力最大值，一旦超过此值则两接触面之间将发生滑移。本文作者对不同的摩擦参数值(范围从 0.05~0.25)都做了计算，但由于在支架扩张过程中，气囊会被挤进支架空隙处，导致支架与气囊之间是很难发生相对滑移的，因此摩擦系数的取值对本文结果的影响并不明显。在本文中，摩擦系数采用 0.2。

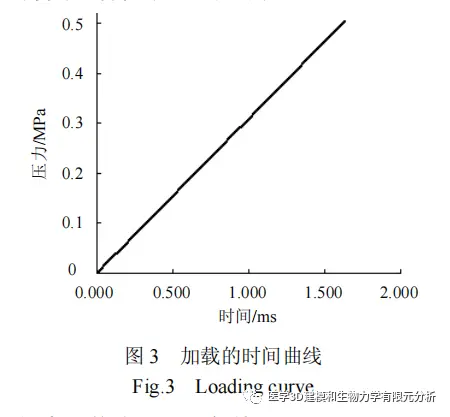
载荷是通过均布压力直接施加在气囊内表面上的。压力大小随时间的变化曲线如图 3 所示。压力以恒定的速度从 0 增加到 0.507MPa。加载曲线的斜率越小，系统产生的动能就会越小。多次尝试不同增压速度，控制系统动能与内能的比值小于 5%。本文计算取气囊的加压时间为 1.635ms。

使用 ABAQUS/Explicit 进行准静态分析，要用慢速运动来模拟静态问题，以避免过快加载导致的局部变形问题。这要求在分析过程中模型的动能不超过内能的 5%~10%。图 6 是加载过程中代表性单胞的动能与内能的比值曲线，在加载过程中这个比值大部分保持在 1%以下，只在初始阶段相对较大，但也是可以接受的。

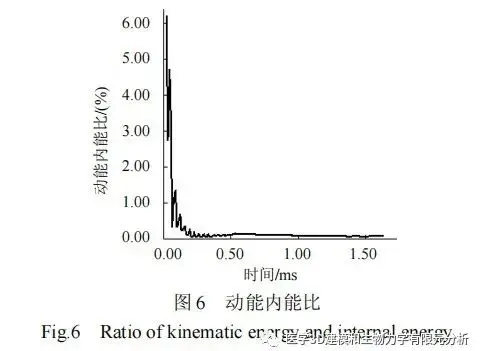
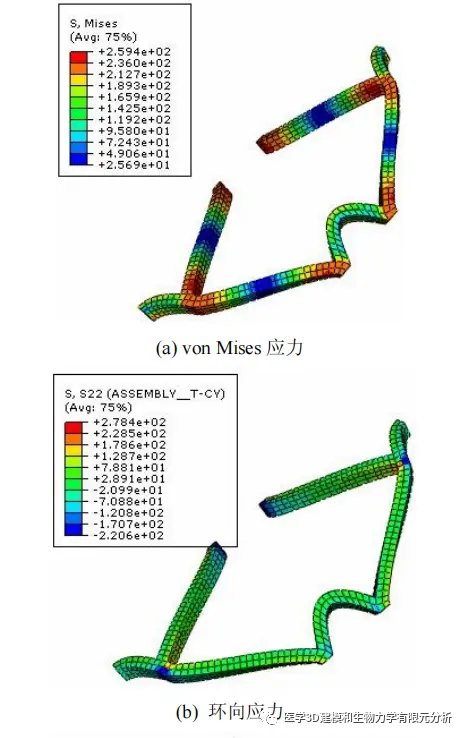
图 7 显示了当加载的压力达到 0.507MPa 时，支架单胞模型的 von Mises 应力、环向应力和轴向应力的分布情况。当内压力为 0.507MPa 时，单胞模型 von Mises 应力最大值为 259.4MPa。从图 7(a)可以看出，支撑筋与连接筋的连接处为应力集中区，应力大小从此区逐渐向支架筋的中部减小。连接筋除了两端与支架筋连接处应力集中很明显外，其他区域应力比较均衡，应力值也只介于 110MPa~180MPa 之间。对于整个单胞模型来说，支架筋中部的应力最小。同时，计算结果还显示，沿环向的变形最大，但环向应力(图 7(b))并不显著，支架筋和连接筋的环向应力值大部分区域都为 28.91MPa。

只有在支撑筋和连接筋的相连处很小的区域里数值较大。由图 7(c)可以看出，支架单胞模型的应力还是以轴向应力为主。在连接筋的拱顶处及支架筋与连接筋的相连处，轴向应力值比其他区域大。这种现象的主要原因是支架沿径向的扩张导致了支撑筋在θ-z 面的弯曲，所以支架应力以轴向应力为主。图 8 显示了支架扩张后外径与气囊压力的关系，图中两条曲线分别是采用单胞分析与整体结构分析得到的结果。可以看出，在加载的初始阶段，支架膨胀得非常缓慢，这是因为加载的初始阶段仅仅是气囊膨胀，随着压力的增加，支架才被气囊撑开。采用单胞分析的方法，当压力达到 0.45MPa 之后，支架的扩张速度迅速加快。当压力达到0.507MPa 时，支架的外径大约为 2.4mm。采用整体结构进行分析时，为了观察支架径向膨胀，所施加的边界条件是，把气囊两端完全约束住，而支架两头放松。因此在支架两头附近的区域，支架的扩张速度比支架中段慢，导致变形后支架两端的直径要稍小于支架中段。图中整体分析的外径值是取支架中段区域扩张直径的近似平均值。在相同气囊压力下，通过单胞分析方法得到的支架外径比整体分析稍大，但相差不超过 0.18mm。

虽然通过单胞分析得到的支架外径比整体分析稍大，但这对于临床使用来说是一个更安全的参考。而从计算成本来对比，单胞模型的单元数与节点数远少于整体的数目，本文作者作一次 V 型支架单胞模型分析时间大约是 1.5h∼2h 之间，而整体分析则需要大约 19h。

在支架随气囊扩张的过程中，轴向长度会随着膨胀而减小。这一行为我们用短缩率来描述，即：

4 结论

(1) 对于承受周期载荷的周期结构，可以只对代表性单胞进行有限元分析，再利用恰当的后处理程序得到整体分析的结果。这里的关键是选取适当的代表性单胞，并对代表性单胞施加恰当的周期边界条件。这种处理方法将大幅减小计算成本。在血管支架的设计中需要进行多种参数的多组数据的反复设计，这种计算量的减小是具有重要意义的。

(2) 对代表性单胞作有限元分析的关键是给定周期边界条件。本文所采用的周期边界条件具有统一的形式，并不对代表性单元的形式选择有任何特别的要求。而且边界条件是以成对边界的位移差的形式给出的，与直接约束边界位移有很大的不同，可以模拟结构变形后边界不再保持平面的情况。

(3) 采用 ABAQUS/Explicit 求解器来分析准静态问题，避免了 ABAQUS/standard 静力分析中容易出现的数值奇异和零主元等使求解难以收敛的情况。但相应的风险是，分析中即使模型本身存在错误也能够得出分析结果。所以在分析前必须保证模型正确，在分析过程中必须保证运动速度比较慢，以保证动能和内能的比例关系在一定范围内。这样才能够保证计算结果是可靠的。

参考文献：

免责声明：文章来源于网络，仅供交流学习，版权归原作者所有。如涉及版权，请联系删除！

PART  01

针对骨学、关节外科、普外科、囗腔科等提供医学力学有限元分析仿真、培训、临床手术模拟分析等；

代做有限元：脊椎、腰椎、颈椎、上下肢、假肢、前臂、血管支架、牙齿、骨关节等；

服务对象：各省市、自治区从事运动生物力学、生物医学工程、基础医学、临床医学、囗腔力学、骨骼力学的教学、研究与应用的教师、科研工作者、各级教练员等方面的相关人员；国内各重点大学、科研院所相关研究领域的博士、硕士相关研究生和学者等。

相关项目代做或课程培训可主页私信小编！