/*仅当作学习笔记,若有纰漏欢迎友好交流指正,此外若能够提供一点帮助将会十分荣幸*/
摘要:在上一篇博文中(利用MATLAB对乐曲进行钢琴演奏【matlab调音_1】),已经简单实现了基于十二平均律的sound函数乐曲演奏,但对音色的处理办法介绍不多,本文介绍几种润色sound函数发声的包络函数。
基本参数设置
利用sound(y,Fs)函数播放声音,其中 Fs代表采样率,设置为Fs=8192(matlab的默认采样率区间为1000-38400,超出这个区间就不能播出声音了)。y代表音频信号矩阵,设f为音符频率,rhythm控制音乐节奏(用于控制每个音符的长度),并且在正弦函数的基础上可得音频信号矩阵y为:
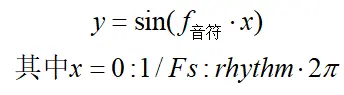
利用包络函数润色发声
为了直观的展示音色处理效果,这里我们依然利用plot函数展示出声音波形,其中原始未经过包络函数处理的声音波形为:图1 未进行包络处理的声音波形
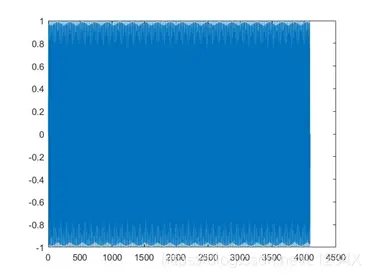
图1 未进行包络处理的声音波形
从图中的波形可以看出,声音几乎没有起伏,声音播放出来人耳也只会听到一段长长的“哔”。这显然是难以接受的,于时在此基础上我们利用包络函数对其进行润色处理。接下来我们将会介绍几种包络函数,并且遵循前文中的基础参数设置。
1 y=kx+b型包络函数
为了细化处理过程,我们将范围缩小到音频信号矩阵y的一个周期范围,其未作处理时
一个周期内生成的波形为
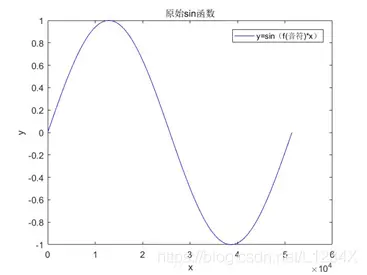
图1.1 未进行包络处理的信号矩阵y的单周期波形
从图中我们可以看到,声音信号遵循着sin函数自己的规律上下起伏变化,这并不符合从发声时声音最强并逐渐减弱的规律。因此,我们引入一个函数来辅助其“衰减”,首先展示y=kx+b型包络函数。
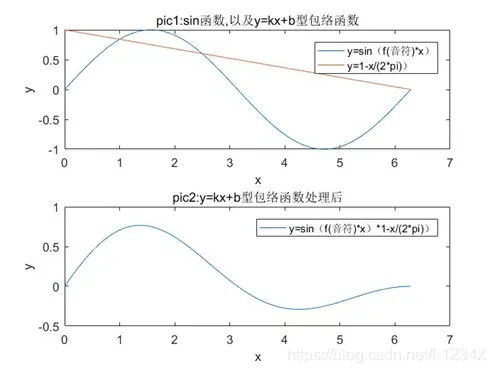
图1.2 y=kx+b型包络函数
从图1.2中的”pic2”可以看到,相比于原始的sin函数,信号y已经有一个随时间衰减的过程了。
经过y=kx+b型包络函数处理的声音波形变为:
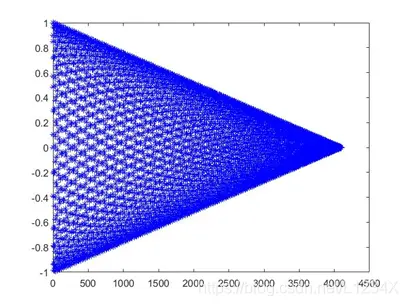
图1.3 y=kx+b型包络函数
与图1相比,可以看到y=kx+b型包络函数处理后的声音波形随时间呈线性减弱。
2 四段直线包络函数
四段直线包络方法,能保证前一个音符能量消失后,才发出后续音符,这样就能有效消除,音符交替时的轻微杂音。四段直线包络方法实现了每个乐音都经过“冲激”“衰减”、“持续”、消失”四个音强变化阶段。由下图可以看出四段直线段构成一次包络,因此只要确定了每段线段的前后端点座标,即可用端点座标求出直线方程,直线方程可以用斜截式通式写出,该四段直线包络技
术将作用于每个音符,所以可用简单的循环,逐个对原有音符的正弦波信号进行包络,最后完成对所有音符的包络。

图2.1 四段直线包络函数
对原始sin函数进行四段包络函数处理后的声音波形为:

图2.2 四段直线包络函数处理后的原始sin函数波形
从图中可以看出,相比于图1.2中y=kx+b型包络函数简单粗暴的衰减,四段包络函数处理办法还原了乐音的“冲激”“衰减”、“持续”、消失”四个音强变化过程。

图2.3 四段函数包络处理后的声音波形
3 exp(-x)型包络函数
在包络函数的处理中最常见的包络函数为指数衰减,最简单的衰减方式是对每个音乘以exp(-x)因子。
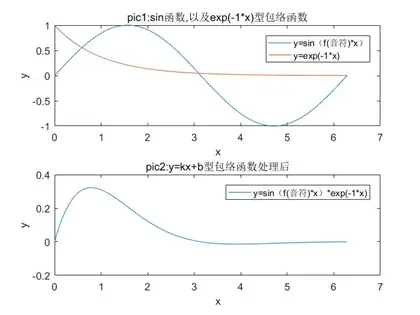
图3.1 exp(-x)包络函数处理后的声音波形
对原始sin函数进行四段包络函数处理后的声音波形为:
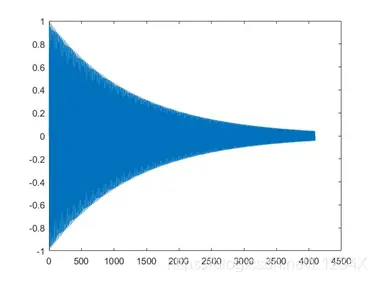
图3.2 exp(-x)包络函数处理后的声音波形
这种处理办法不管是什么音符,都采用相同的衰减速度,通过人耳判听,可以发现噪音减弱但并没有消除,所以播放的音乐效果不是很好,同时还感觉音乐起伏性不强。
4 exp(-kx/rhythm)型包络函数
针对exp(-x)型包络函数处理方式的缺点,根据乐音音长标识来确定衰减速度的快慢,于是我们引入rhythm控制节奏。音长越长的乐音哀减越慢,音长越短的乐音衰减越快。
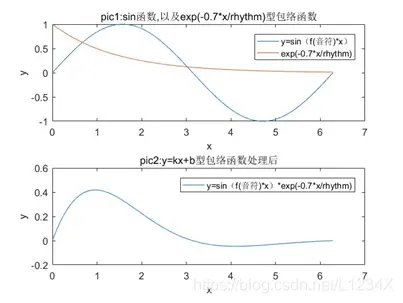
图4.1 exp(-kx/rhythm)型包络函数处理后的声音波形
对原始sin函数进行四段包络函数处理后的声音波形为:
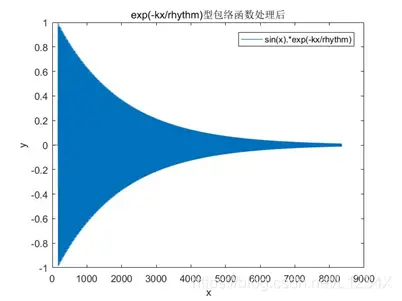
5 x/exp(-kx/rhythm)型包络函数
x/exp(-kx/rhythm)型
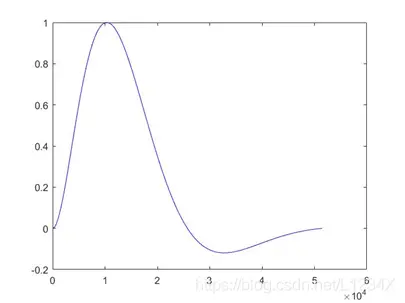
对原始sin函数进行四段包络函数处理后的声音波形为:
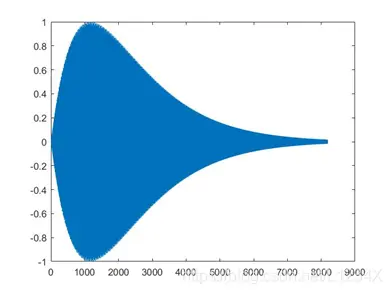
图5.2 x/exp(-kx/rhythm)型包络函数处理后的声音波形
x/exp(-kx/rhythm)型包络函数处理后的声音波形相比其它更加圆润,最终的效果也更好。