要程序优惠可私信说图号。兄弟们助我一把,我筹饷能干票大的——让物理光学说人话。

一、单缝的夫琅禾费衍射 夫琅禾费衍射的装置,以单缝、点光源为例的2维视图:
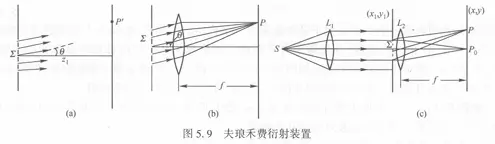
图1 引用自梁铨廷《物理光学第5版》
其3维视图:
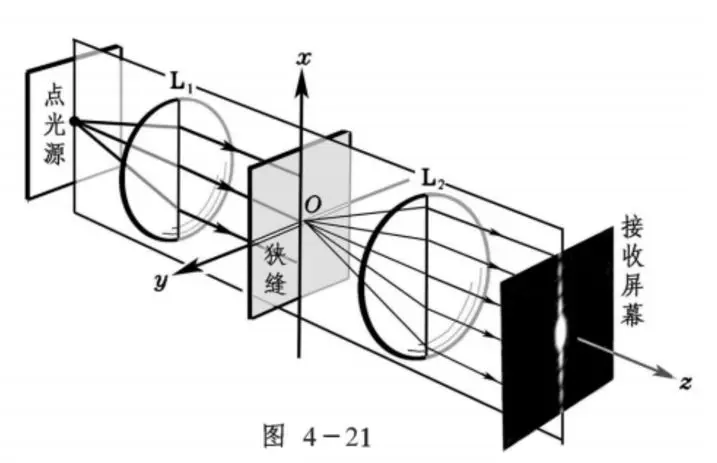
图2 引用自赵凯华《新概念物理 光学》
这里有时候会考简答分析: 【考试题目】单缝夫琅禾费衍射装置中,点光源上下左右移动,对条纹的影响是怎样的?
【分析】产生影响源于光程差的改变,具体来说,是狭缝两个端点的光程差与零级强,在源-缝上抄了近路,在缝-像上就要绕远路来汇合于零级强。所以衍射条纹向点光源移动方向移动。如此以来,与狭缝平行的线光源会形成与狭缝平行的条带,极次增大方向仍⊥狭缝:
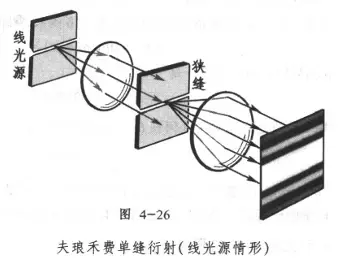
图3 引用自赵凯华《新概念物理 光学》
我们可以用傅里叶变换法模拟上述过程:
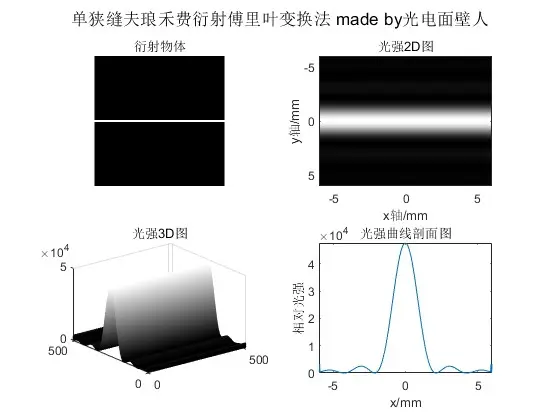
图4 傅里叶变换法模拟单缝夫琅禾费衍射
除了傅里叶变换法,我们还考虑如下几种方法:
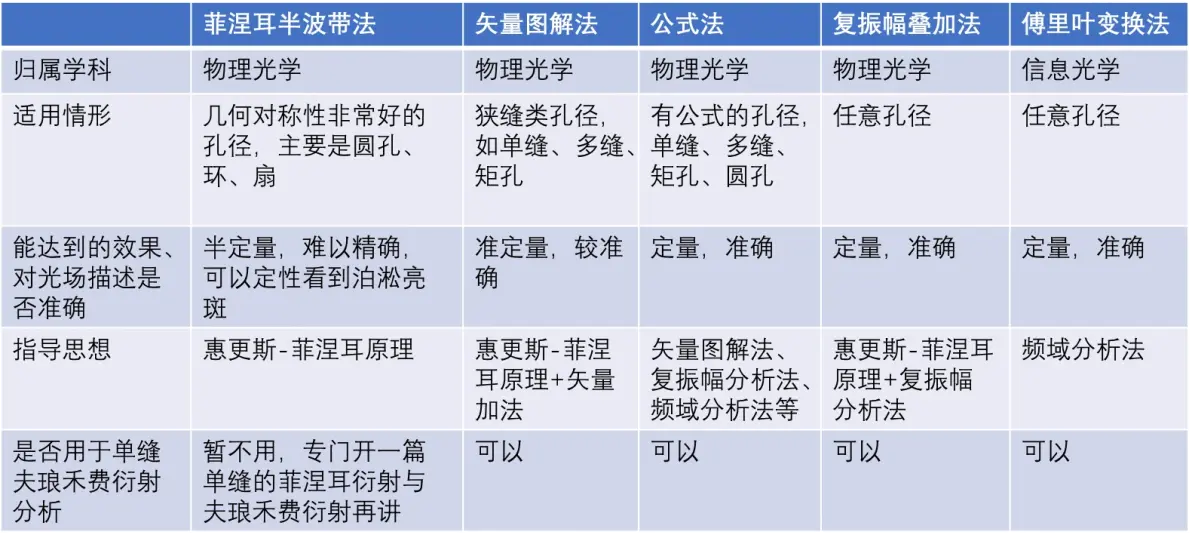
表1 布置作业时常见的衍射分析法
其中,菲涅耳半波带法在另一篇专栏中会提到,在此不展开。
公式法(课本中一般用矢量图解法推导):
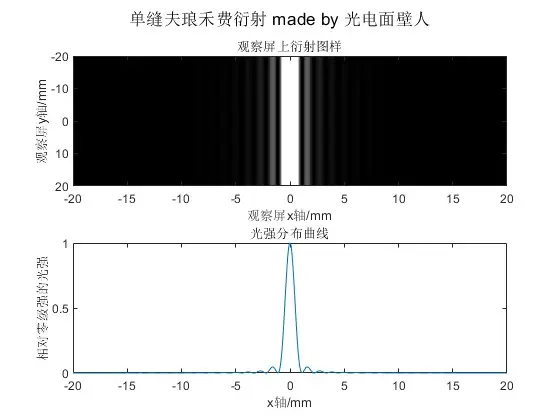
图5 单缝夫琅禾费衍射公式法

详细注释版适合新手

其公式由来过程:

图6 引用自赵凯华《新概念物理 光学》
由矢量图解,合振幅Aθ是零级直射振幅A0乘sinc函数,如果没有这个几何关系,那么Aθ=元波带小矢量的叠加,就不一定能严格=2Rsinα了。以α=π/2为例,此时正确的Aθ应当=2R,但元波带小矢量叠加起来的结果是渐进的:
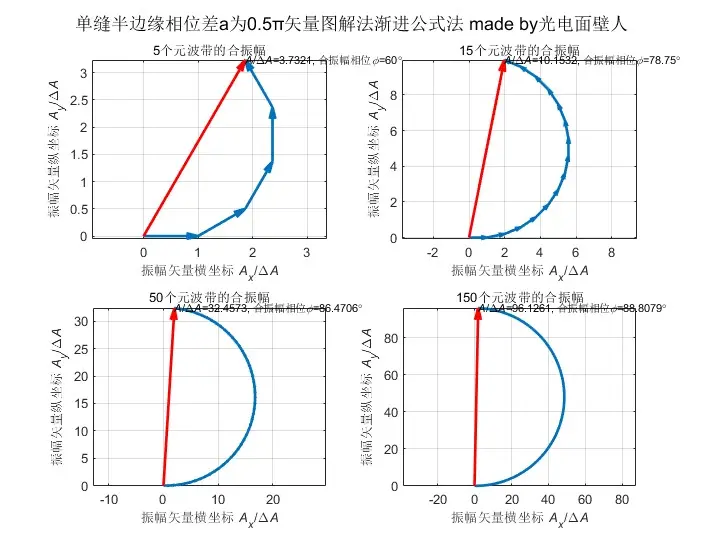
图7 矢量图解法示意

这也是为什么我在表1中称矢量图解法是准定量的,矢量图解法是菲涅耳半波带法的精细版,即元波带法,越微元越准确,这启示我们在编程时也可以不套公式,用微元复振幅直接叠加法:
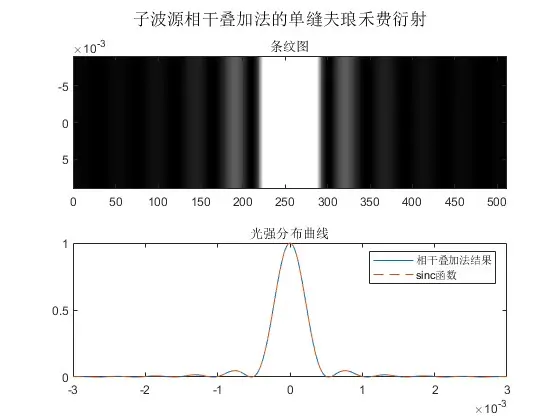
图8 单缝夫琅禾费衍射复振幅叠加法

我们可以看到微元复振幅叠加法和公式法二者等价。这在课本中也有所印证:
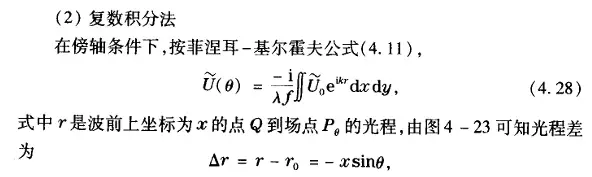
图9 引用自赵凯华《新概念物理 光学》

图10 引用自赵凯华《新概念物理 光学》
复振幅叠加法还有一种写法是这样的:
%B表示合光强
for i=1:n
sinphi=ys(i)/f;
u=pi*yp*sinphi/lambda;
sumcos=sum(cos(u));
sumsin=sum(sin(u));
B(i,:)=(sumcos^2+sumsin^2)/n^2;
end这个cos和sin的意思是将复振幅分解为实部和虚部,但这种写法比较古早了。直接用复振幅描述起来更直观。
衍射条纹的形状主要取决于波长和缝宽,编写一个简易的GUI:
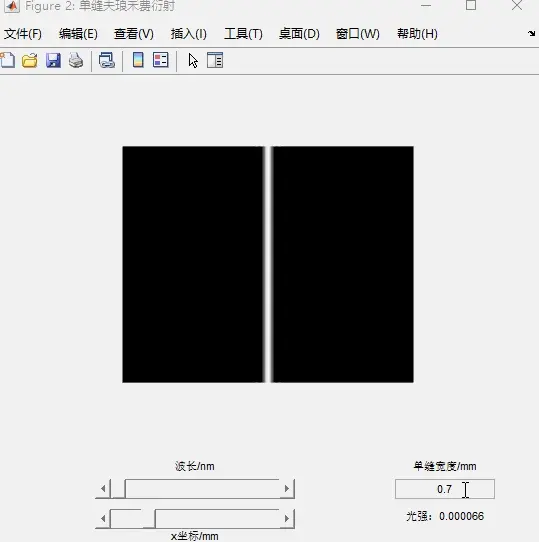
图11 单缝夫琅禾费衍射,脚本生成简易GUI

波长越大、狭缝越窄,条纹越宽,能实时显示当前位置的相对光强。调节亮度可以看清次级大,编写另一个GUI来优化:
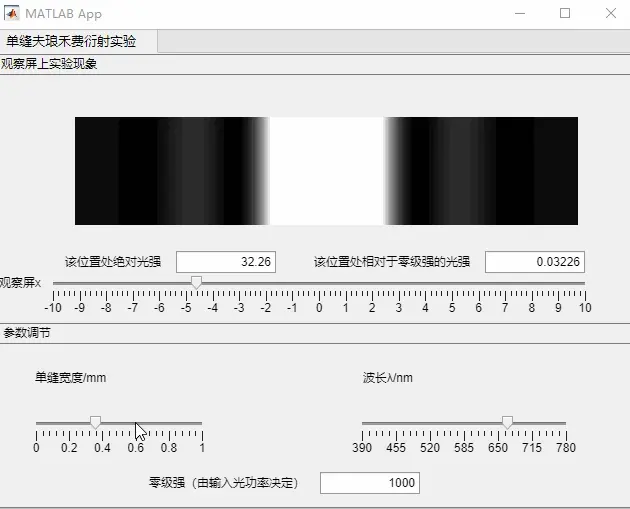
图12 单缝夫琅禾费衍射App1
app非必要的就不用管了,图一乐,需要的话请私信。 可以再添加相对光强曲线:
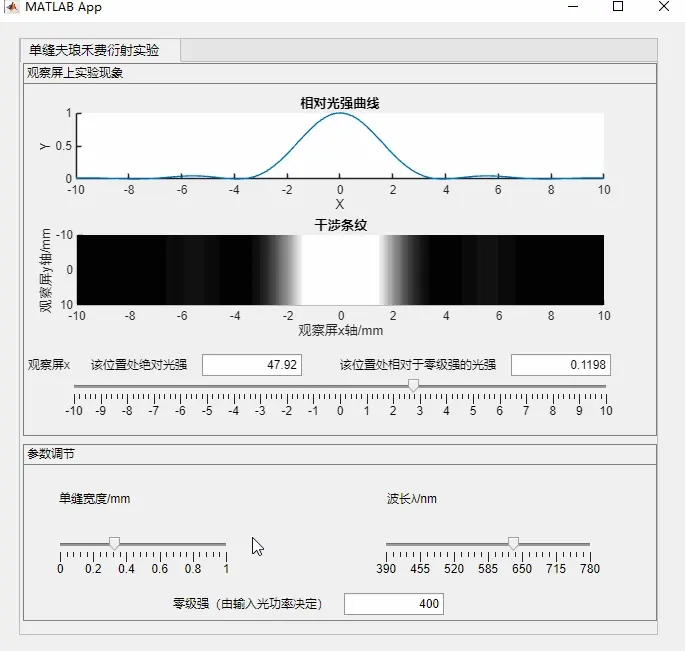
图13 单缝夫琅禾费衍射App2

二、矩孔的夫琅禾费衍射 矩孔衍射是单缝衍射的2维版本:
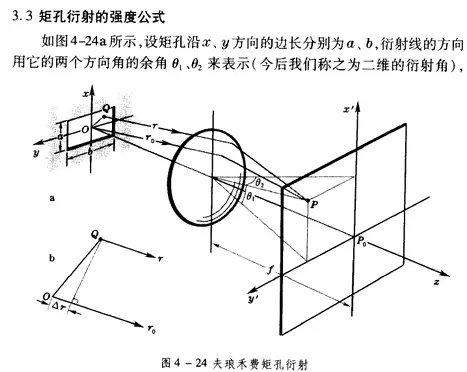
图14 引用自赵凯华《新概念物理 光学》
编写一个简易的GUI,矩孔宽度改变,其衍射图案伸缩反应在长度方向上:
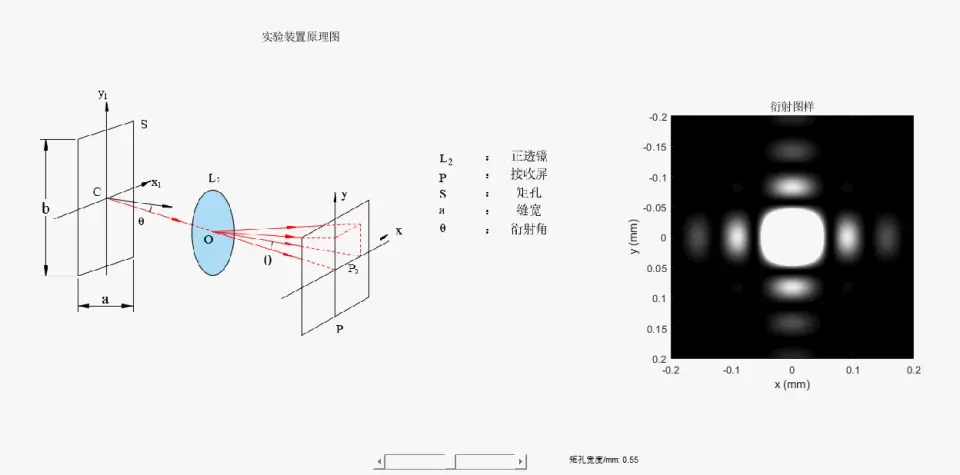
图15 矩孔夫琅禾费衍射改变宽度
提高亮度,方孔时的衍射图案如下:

图16 正方形矩孔的夫琅禾费衍射图案

可以看到十字形簇拥的次级大们。如果想放大图案,可以延长观察透镜焦距:
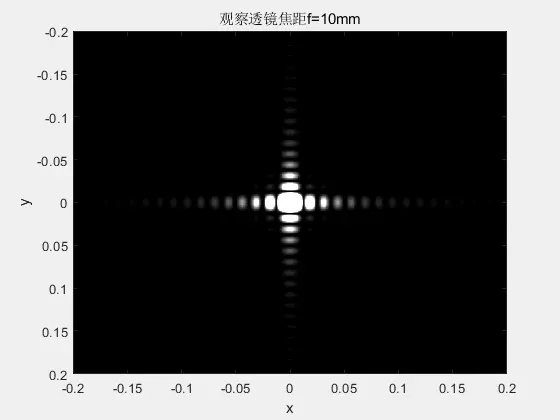
图17 矩孔的夫琅禾费衍射延长焦距放大图案
一键运行程序导出GIF保存至本地,如图17。

如果用傅里叶变换法,是等价的结果:
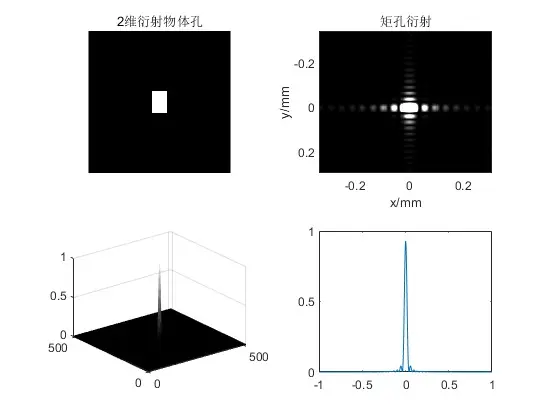
图18 傅里叶变换法模拟矩孔的夫琅禾费衍射


三、多缝的夫琅禾费衍射
我们已经会了单缝的情形,双缝衍射的情形要考虑双光束干涉
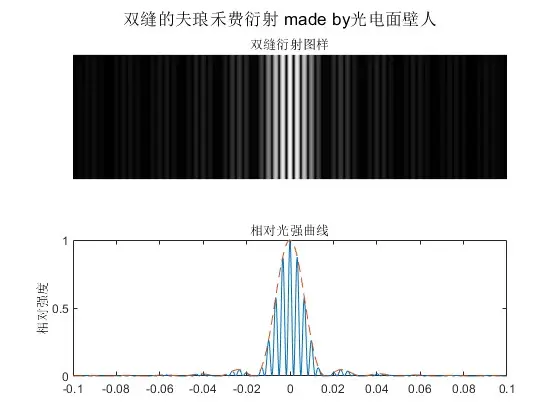
图19(a) 双缝衍射
我们可以看到类似于杨氏双缝干涉傍轴区的平行等距直条纹,按单缝衍射起伏。在近轴区:
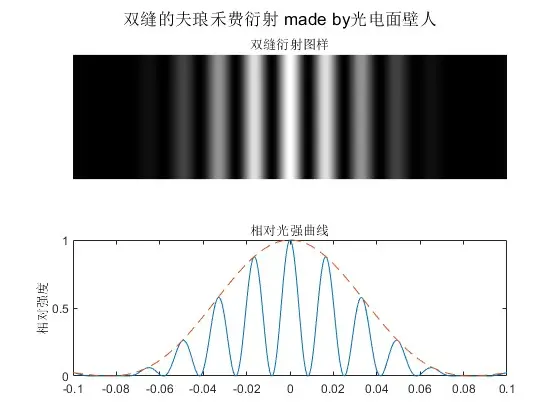
图19(b) 双缝衍射近轴区

如果是多缝衍射其衍射条纹为:
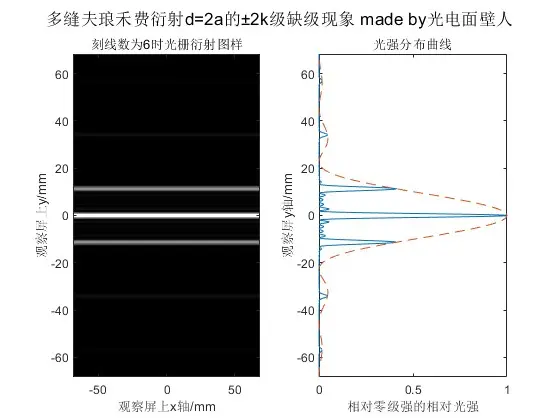
图20 多缝的夫琅禾费衍射

缺级是衍射零点与干涉主极大重合,导致干涉主极大不显现。干涉主极大的包络是单缝衍射的形状,如图中虚线所示。 单缝与多缝衍射的区别:

图21 引用自蔡履中《光学》第三版
第(1)(3)已经可以较容易看出,于是我们取消光强归一化,有:
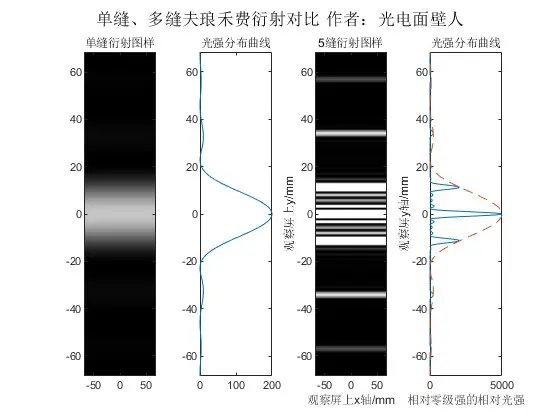
图22 单缝与多缝夫琅禾费衍射对比
我们可以看到,N=5缝的零级强=N²倍单缝的零级强。 当缝数N很大时,就是光栅衍射,其光栅方程为:d(sinθ+sini)=mλ 当斜入射的时候,条纹向光源移动反方向补偿移动,比如光源上移则条纹下移:
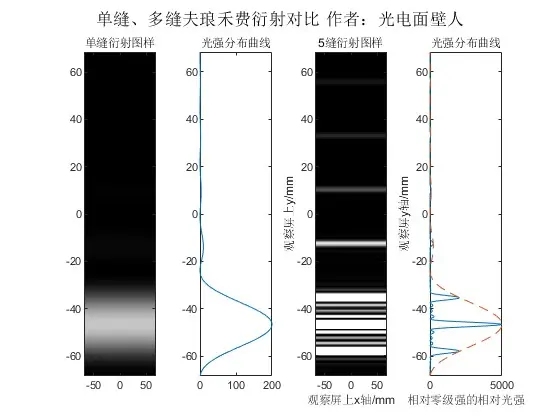
图23 单缝与多缝夫琅禾费衍射斜入射时的情形

光栅的另一个作用是充当色散元件,由于其主极大半角宽度是∝波长,所以不同波长的同级主极大在位置上相互错开,以单缝夫琅禾费衍射在白光入射时为例:
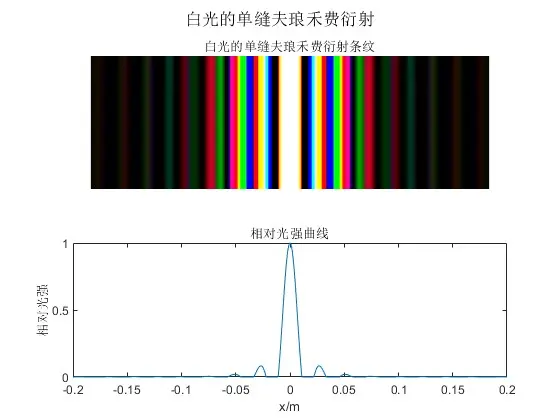
图24 白光入射单缝夫琅禾费衍射
我们可以看到,只有零级强是白光,第一级次分光。同级次红光在外,紫光在内。如果是白光入射多缝的夫琅禾费衍射:
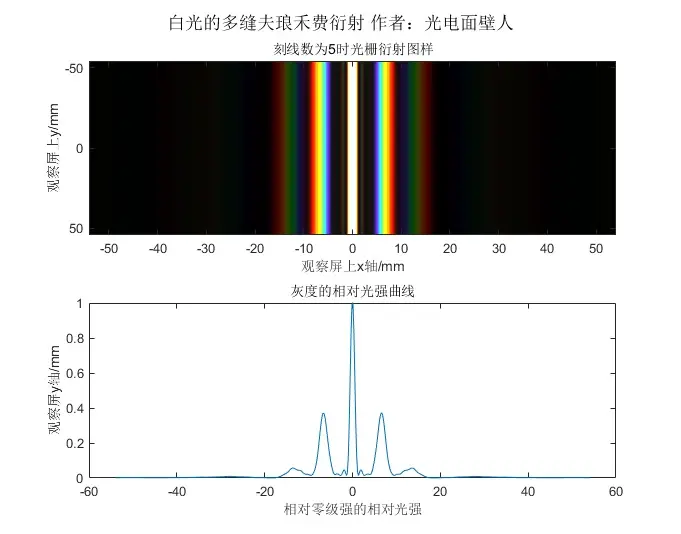
图25 白光入射多缝夫琅禾费衍射
可以看到,多缝时只有第一级次的被凸显。白光干涉衍射、色散分光的另开一个专栏单独讲。