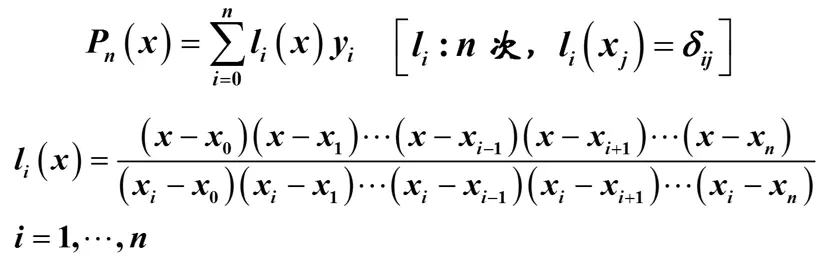MATLAB基础教程：第四讲核心内容

在进行文件数据读取，并进行数据预绘图后，非真实值数据点经常出现，不论是缺失还是数据自动设定的情况。Matlab绘图中线性为"-"(折线图)时，若有缺失，则对应位置标记为NaN(not a number，即不是一个数)，而自动设定的非真实记录数据，明显地脱离“群体”，而且都是以一个特别大或特别小的数字出现，如：-999等。

首先，便是要先找到对应数列中(为程序中数列对应的变量)存在非真实值的数据点位置，借助或即可实现，找到对应要预处理的位置后，通常需要去除非真实值数据点。虽然可以利用循环一一实现，但Matlab可以直接对相关数列做逻辑运算，因此用“隐藏查找”的形式直接统一处理：或。注意：[]是置空符号，相当于清楚对应位置变量，数据长度会发生变化，比较“粗鲁”；对应矩阵不建议进行此操作，因为矩阵容易出现每一行或每一列size发生改变，而相应合理应该是将-999位置变为NaN的形式后，再结合等进行一些基本统计量的计算。

再者，找到对应位置或删除一些不需要的数据点后，有时需要在对应位置重新做插值(一般来说，数量都不太多；如果数量太多，如超过样本量的1/3甚至1/2，也不是很建议做插值，因为插值引入的误差会大大影响分析的结果讨论)，来保证每个测量量之间的间隔时间是一样的，而不会出现大量不好处理的“非等间隔”数据。下面主要来介绍多项式插值和Lagrange(拉格朗日)插值。

• 多项式插值函数：polyfit、polyval和poly2sym【调用案例】>>x1=[1,2,6,10]; y1=[3,2,8,9];>>P=polyfit(x1,y1,3); %用三次多项式，确定插值函数P(降幂形式)>>X=1:0.01:10; Y=polyval(P,X); %构建新数据点X(包含插值点位置)，利用P计算对应值Y>>plot(x1,y1,'ro',X,Y) %画图>>Func=ploy2sym(P) %给出多项式形式
• Lagrange插值公式的Matlab实现一般情形Lagrange插值公式给出如下：

图一. 一般情形Lagrange插值公式

1. 注意到函数的分子和分母对应了插值位置和原先所有插值节点之间的关系，由于两者基本一致，而且都是连乘的形式，考虑使用prob函数；
2. 程序定义向量中，令x：插值位置；x_ori：插值节点；由x_ori~=x_ori(i)给出式子中规避连乘的间断项；作差由x-x_ori(x_ori~=x_ori(i))给出；结合连乘符号，则有prob(x-x_ori(x_ori~=x_ori(i)))；
3. 因此，分子和分母分别为：pob(x-x_ori(x_ori~=x_ori(i)))；prob(x_ori(i)-x_ori(x_ori~=x_ori(i)))
4. 则l(i)=pob(x-x_ori(x_ori~=x_ori(i)))/prob(x_ori(i)-x_ori(x_ori~=x_ori(i)));
5. 在l和y都是列向量的前提想，P=sum(l.*y)或P=l’*y。

同时，Matlab也提供了各种维度的插值函数，下面进行一一讲解，在高维插值时，要注意网格点的生成，基本有两种生成函数，注意区别：ndgrid和meshgrid。这样生成的网格节点是大小均匀的分布、便于数据处理、区域综合分析，但存储量大，不适用于稀疏空间数据，与之相对的是一般分布。

• 一维：interp1、csapi和fnplt(1) >>y=interp1(x,y,xx,'method',['extrap'])%x：插值节点；y：节点函数值；xx：插值位置%‘method’可选择有：%spline        三次样条函数插值%v5cubic     三次多项式插值%linear        线性插值%nearest     最邻近插值%pchip        分段三次Hermite插值%extrap       可选择添加，以防止有外插的点；默认只能做内插(2)>>S=csapi(x,y)%三次样条插值; fnplt(S);%拟合结果绘制%x/y同(1)，S返回样条函数对象的插值结果，是一个结构形式(元胞)的数据，包括子区间点、各区间点插值函数系数等。
• 二维：interp2、griddata(1) >>Zi=interp2(X,Y,Z,Xi,Yi,'method');% 插值点Xi ,Yi 可以是向量或同维矩阵% X与Y 须是单调的，Z的维数为Y×X% 若Xi与Yi 中有在X与Y范围之外的点，则相应地返回NaN%‘method’可选择有：%spline        三次样条函数插值%cubic         双三次插值%linear        双线性插值算法(缺省时默认)%nearest     最邻近插值(2) >>z=griddata (x0,y0,z0,x,y,’method’); %二维一般分布插值%‘method’可选择有： %v4            4.0提供的插值算法，公认效果较好%cubic         双三次插值%linear        双线性插值算法(缺省时默认)%nearest     最邻近插值
• 三维：griddata3(类比griddata2的过程，用之前用meshgrid生成三维网格)           interp3(类比interp1/2的形式)>>V0=interp3(x,y,z,V,x0,y0,z0,'method');>>slice(x0,y0,z0,V0,[-0.5,0.3, 0.9],[0.6,-0.1],[-1,-0.5,0.5,1])% 仅画出指定坐标格点上的函数值，也称作查看“切片细节”
• N 维：interpn、griddatan

可以发现，其实在做插值的过程中，无论是什么插值方法，自然地就存在基于数据点的一些拟合逼近过程，但这种“拟合”和后续的拟合有一些不同，前者是插值方法带来的，后者可以是参数化的、也可以是非参数化的，可以是人为给定的、也可以是非人为给定的，有些特定情况也称这种拟合是“线性回归分析”（无论是一元的，还是多元的），这种概念的拟合范围更广更丰富。但是，不可忽视的是，每种插值方法都有其一定的误差，因此对于误差及其传递的分析也很重要。