讲解视频:可以在bilibili搜索“MATLAB教程新手入门篇——数学建模清风主讲”。

break 和 continue 也是MATLAB中的关键字,它们可以更加灵活地控制循环过程的执行。在MATLAB中,break和continue只能与for循环或while循环一同使用,不能用于其他场合。下面我们来简要介绍一下 break 和 continue 的用法:
下面我们来看两个简单的案例:
(1)已知 ,当n最小取多少时, y的计算结果大于10?这个例子在while函数中出现过,下面我们尝试使用for循环求解。
y = 0;
for n = 1:1e8
y = y + 1/n;
if y > 10
disp(n)
break % 退出for循环
end % if配套的end
end % for配套的end使用for循环需要通过向量或者矩阵给出循环的次数,由于我们这个问题的循环次数是未知的,因此可以预先给一个很大的循环范围,我们这里给定n为1至1×10^8构成的向量。
如果在循环体中找到了我们所需的结果(即y大于10),就可以通过break关键字退出循环。通常情况下,判断条件是否成立需要用到if语句。
(2)使用循环输出1至10中所有的奇数。
for i = 1:10
if mod(i, 2) == 0
continue
end
disp(i)
end在每次迭代中,使用mod(i, 2)来检查 i 是否为偶数。如果 i 是偶数,那么 mod(i, 2) 的结果将为0,这时会执行continue,直接跳到下一次迭代,因此当i为偶数时,代码后面的disp(i)不会被执行;只有i为奇数时才会被输出。
思考:如果不使用continue关键字,代码应该如何修改?
注意,如果存在循环的嵌套,break和continue 仅在调用它的循环的主体中起作用。即break 仅从它所发生的循环中退出,continue 仅跳过它所发生的循环体内的剩余语句。
下面我们来看一个典型的例子,该例子中有两个for循环,因此存在循环的嵌套,我们称第一次出现的循环为外层循环(简称外循环),第二次出现的循环称为内层循环(简称内循环)。另外,在内循环中我们加上了if条件语句,并在if的条件不满足时使用了break关键字,此时的break由于出现在内循环中,因此在起作用时仅会跳过内循环,外循环会继续下去。
for ii = 1:2 % 外循环
for jj = 1:3 % 内循环
if jj <= ii
disp(ii)
disp(jj)
else
break
end % if配套的end
end % 内循环配套的end
end % 外循环配套的end
上面这段代码详细的计算思路如下:
1. 外层循环(由变量 ii 控制,ii = 1:2)首先从 ii 的值1开始。
2. 内层循环(由变量 jj 控制)在每个外层循环迭代内部执行。
3. 在外层循环的第一次迭代(ii 等于1)内部,内层循环(jj = 1:3)执行。
4. 外层循环的第二次迭代(ii 等于2)开始。
5. 再次进入内层循环(jj = 1:3),jj从1重新开始。
在实际编程中,break的使用频率远高于continue,下面我们来看几道典型例题。
(1)质数(Prime number),又称素数,指在大于1的自然数中,除了1和该数自身外,无法被其他自然数整除的数(也可定义为只有1与该数本身两个正因数的数)。给定任意一个大于100的自然数n(例如n=135389),请判断n是否为质数。
思路:我们可以遍历从2到n-1的所有整数,检查它们是否能够整除n。如果找到任何一个能够整除n的整数,那么n就不是质数;否则,n就是质数。
n = 135389; %要判断的数n
is_prime = true; % 初始化标志变量is_prime为true,此时代表n是质数
for ii = 2:n-1 % 思考:如何缩小循环遍历的范围来提高代码运行的效率,留作本章课后习题
% 检查ii是否能够整除n
if mod(n, ii) == 0
% 如果能整除,则n不是质数,将标志变量is_prime重新赋值为false
is_prime = false;
break; % 跳出循环
end
end
disp(is_prime)
(2)一副扑克牌有54张牌(桃杏梅方四种花色的A 2 3 4 5 6 7 8 9 10 J Q K加双王),假设三名玩家玩斗地主,其中地主有20张牌,两个农民各17张牌。若你是其中一名玩家,且你每次都选择当农民。,请编程模拟以下场景:先玩第一把,若这把手上有炸弹则这把玩完后下场换其他人玩;若手上没有炸弹则继续玩第二把,直到玩到第k把时手上有炸弹,此时玩完这一把后下场换其他人玩。请输出你模拟的k。注意:假设每把牌都洗的足够的混乱,确保为无序;有炸弹是指手上有双王或者有四张相同的牌例如4张3。(这里的k表示你作为农民首次出现炸弹的轮数,由于发牌过程是随机的,那么k肯定也是一个随机的变量,即每次模拟的k可能都不相同。比如运气好可能第一把就出现了炸弹,此时k等于1,运气不好可能需要好多把才会出现炸弹,此时k较大)。

思路:由于循环的次数不定,因此我们可以使用while循环来不断模拟游戏的进行,直到满足退出的条件。在每一轮中,我们作为农民会随机抽取17张牌,并检查是否有双王或者普通的炸弹。如果有任何一种炸弹,就会退出循环,否则会增加游戏的轮数,继续下一轮。最后,我们可以输出模拟的k值,表示玩到第k把时手上有炸弹。
% 用1至13分别代替A 2 3 ... J Q K, 重复4次表示四种花色;用14和15分别代表大小王
poke = [repmat(1:13,1,4),14,15]; % 生成一副扑克牌
k = 1; % 玩了多少把游戏
while 1
% 从1:54中随机抽取17个数,表示17张牌对应的下标
idx = randperm(54,17); % randperm函数的用法:《第3章:课后习题讲解中拓展的函数》
% 发牌并排序(排序后牌面看起来更清楚一点,事实上不排序也不影响下面的代码)
p = sort(poke(idx));
% 检查是否有大小王
v1 = all(ismember([14,15],p)); % v1为true表示有双王,为false表示没有双王
% 检查是否有普通的炸弹
v2 = false; % v2表示是否有普通的炸弹,先假设没有,因此初始化为false
for ii = 1:13
if sum(p == ii) == 4 % 如果有四张一样的牌
v2 = true; % % 将v2赋值为ture,表示有普通的炸弹
break % 只要有一个普通的炸弹就可以退出for循环了
end
end
if v1 || v2 % 如果有王炸或者普通炸弹就可以退出while循环
break % 跳出while循环
else
k = k + 1; % 没有炸弹就再玩一把
end
end
disp(k) % 输出首次出现炸弹时玩的轮数在本题中,既用到了while循环又用到了for循环,且出现了两个不同用途的break,大家课后一定要认真消化,并尝试自己求解这个例题(当然,判断是否存在普通的炸可以不用循环语句,我们在第三章的课后习题中有讲解,详情请看第三章课后习题挑战篇的Q5)。
另外,本题还能继续扩展下去,例如重复上面的模拟过程N次(N可以设置得大一点,例如N等于10万),得到这N次模拟结果的k,并计算这N次k的平均值,这个平均值就能表示你作为农民首次出现炸弹所需的期望轮数。这个拓展的问题将留作本章最后的课后习题,我们下一道题也会介绍类似的思想。
(3)一只失明的小猫掉进山洞里,山洞有三个门,其中进入第一个门后走2h后可以回到地面,进入第二个门后走4h会回到原始的出发点,进入第三个门后走6h还是回到原始的出发点。假设小猫每次都随机地选择这三个门中的一个进入,求小猫走出山洞的期望时间?
思路:在上一章的课后习题中,我们见到过类似的题目,当时我们介绍过蒙特卡罗模拟这种方法,蒙特卡罗模拟将所求解的问题同一定的概率模型相联系,用计算机实现统计模拟或抽样来获得问题的近似解。我们可以模拟这个过程N次(N一般要设置的大一点,例如让N等于10万),每次模拟中我们都让一只猫走出山洞,并记录下这只猫所需的时间。接下来我们只需要对这N次模拟结果得到的时间计算平均值,就能估计小猫走出山洞的期望时间。
N = 100000; % 设置模拟的次数
T = zeros(N,1); % T用来存储每次模拟得到的时间
for ii = 1:N % 开始进行 N 次模拟
t = 0; % 初始化时间
while 1 % 开始模拟小猫走出山洞的过程
choose = randi(3); % 随机选择第几个门
if choose == 1 % 选择第1个门
t = t + 2; % 走2小时回到地面
break % 小猫成功走出山洞,结束模拟
elseif choose == 2 % 选择第2个门
t = t + 4; % 走4小时回到原始出发点
else % 选择第3个门
t = t + 6; % 走6小时回到原始出发点
end
end
T(ii) = t; % 记录每次模拟得到的时间
end
mean(T) % 计算所有模拟结果的平均值,即小猫走出山洞的期望时间的估计
(4)这个例题我们介绍二分搜索法求函数零点。若函数f(x)在区间[a,b]上连续严格单调,且满足f(a)×f(b)<0,那么f(x)在区间[a,b]上有且仅有一个零点。
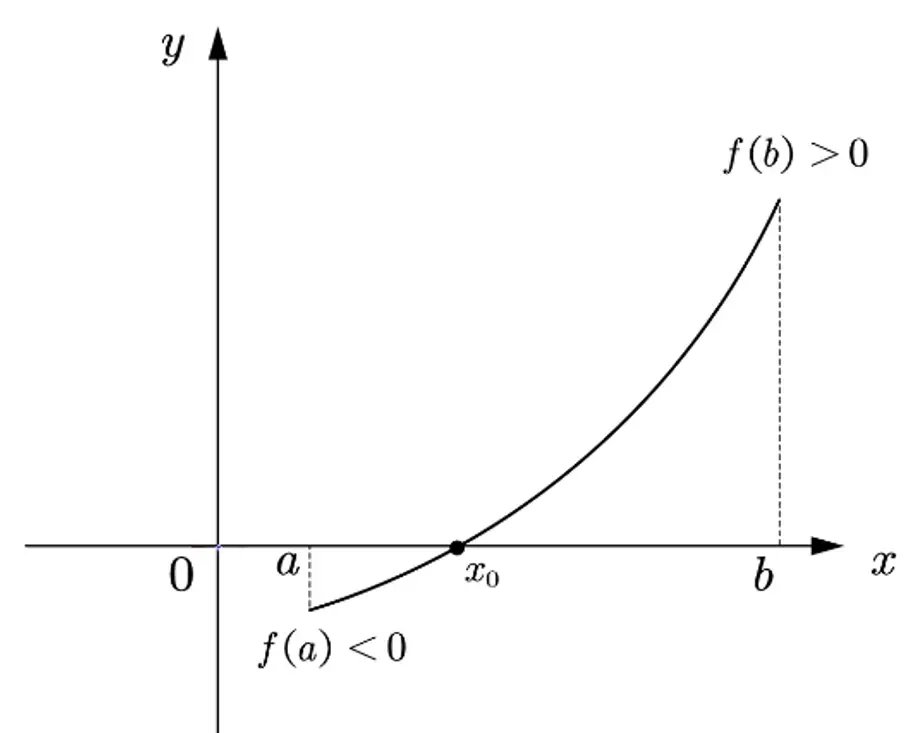
二分搜索法的基本思想是不断将区间[a,b]一分为二,然后判断零点位于哪一半区间内,接着继续将包含零点的那一半区间一分为二,如此循环,直到得到足够精确的零点的估计值。以下是二分搜索法的一般步骤:
步骤1:选择函数零点所在的初始区间[a,b],确保f(a)×f(b)<0。
步骤2:计算区间的中点c = (a + b) / 2,并计算函数在c处的值f(c)。
步骤3:如果f(c)的值恰好等于零,或者f(c)的绝对值小于某个给定的误差阈值,那么c就可以当成零点,迭代结束。
步骤4:如果f(c)与零的差异较大,那么需要根据f(c)的正负号,将原来包含零点的区间[a,b]更换为[a,c]或[c,b],确保零点仍然在新的区间内(例如: f(a)×f(c)<0则更换为[a,c])。
步骤5:重复步骤2到4,直到找到零点或者达到所需的精度停止迭代。
下面看一个具体的题目:函数, f(x)在区间[6,10]严格递增且f(6)< 0 ,f(10)>0,请用二分搜索法求零点
(
和0的误差控制在1e-8内即可)。
% 设置初始搜索区间
a = 6; b = 10;
% 设置误差阈值
epsilon = 1e-8;
% 开始二分搜索
while 1
% 计算区间中点
c = (a + b) / 2;
% 计算中点处的函数值
fc = c^3 - 8*c^2 + c - 5;
% 如果中点处的函数值已经足够接近零,停止搜索
if abs(fc) < epsilon
break
end
% 否则根据函数值的正负来调整搜索区间
fa = a^3 - 8*a^2 + a - 5;
if fa * fc < 0 % f(a) × f(c)<0
b = c; % 区间更换为[a,c]
else % f(c) × f(b)<0
a = c; % 区间更换为[c,b]
end
end
% 找到的零点估计值
x0 = c;
disp(x0)

下一篇文章:
更多文章可点击下方合辑: