当然整个建模到出结果花了我8个小时时间.......

看到GM的 这期视频里的玉米拼图,我发现这个结构还是比较简单的,应该可以用比较简单的数学模型建模出来然后求解,正好回顾一下去年学的数值最优化课程。

视频中玉米拼图部分截图
当然我手头并没有这个拼图,所以一共要分为根据GM的视频推测出玉米拼图的具体结构,按照结构来进行数学建模,求解模型并转换回到拼图结果三个部分。
这里略去玉米拼图的介绍(包括转换为二维拼图的部分),还请先看完GM的 这期视频后再来看后面的部分。
拼图结构
视频并没有直接呈现出每块拼图的结构,但是还是能够通过GM拼图的过程(有剪辑),以及其给出的二维的结果(有一个小错误,实际是完全铺满的),来推断出来每个拼图块的具体结构。

二维的结果,没有做颜色区分所以还是不知道具体结构
根据视频推测出来的具体结构
这里就不讲具体的推测过程了,整体不是很难但是也需要一些逻辑推导,这也是一个puzzle呢
值得注意的是,这里水平的一格对应了实际拼图中的两颗玉米粒,这是由于实际拼图都是两个两个玉米粒在一起的。
建模部分
这里每个玉米片的状态是有限的,并且不算特别多,所以会比较好建模。
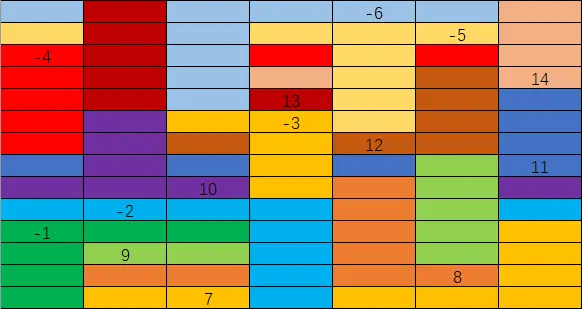
这里需要让玉米片平铺整个平面,自然需要计算某一个位置的玉米粒的数目(这里以拼图中的两颗玉米粒为一个)。由上,对于给定的一块玉米片(i),其处于某一个状态(j,例如在第1层,旋转了2个单位,正向朝向)时,在位置(α,β)处的玉米粒数目我们是可以知道的,记为:
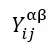
将不同状态的结果写到一起,应该满足这样的关系:
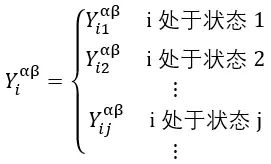
而考虑所有的拼图贡献,最终处于位置(α,β)处的玉米粒数目应该将其加起来:
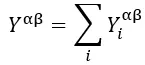
这样全部铺满则需要对于所有的(α,β),上结果都为 1,也就是:
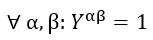
上述状态的选择可以使用变量来实现,这里使用这样的方法:
把某个玉米片(i)是否处于一个状态(j)记为 Pij,Pij=1 表示其处于这个状态,而 Pij=0 表示不处于这个状态。这样上述状态选择就可以使用乘积求和的方式来表示:
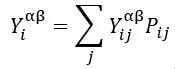
其实就是将其建模成0-1整型规划问题,是数学建模中非常常见的模型
则上述拼图问题就是寻找合适的一组 {Pij},使得其满足:
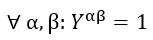
当然这里 Pij 还需满足一些约束条件,一个是每个玉米片只能选择一种状态(这是所有0-1整型规划问题都要求的),也就是对于某个固定的 i,对于所有的 j,Pij 有且只有一个为1(其余都为0),可以写成等价的公式形式(其和为1):
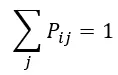
还有一点是对于这个拼图,每一层都只能有一个玉米片,并且层数刚好等于玉米片数(都为14),也就是每层都有且只有一个玉米片,即在同一层的 Pij 中也有且只有一个为1:
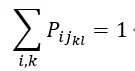
其中 l 表示层数,k 为与层数无关的角标,这里意思就是对相同层数内的 Pij 的一个求和。
这样整个模型就构造完成了,剩下的是所有状态下 Y 的计算了。
在开始之前先确定所有的状态数,一般来说,对于一个玉米片,其可以处于上下共14层,旋转一共7个单位(以两颗玉米为一个单位),以及正反2种,共196种状态。
再考虑到一共有14个玉米片,所以变量 Pij 的数目就一共有2744个。这个数目当然不可能穷举求解,不过现代的整型线性规划求解器(这是一个整型线性规划问题)求解这种规模的问题还是很轻松的。
Y 的计算
这里将 Y 写成矩阵的形式,这样矩阵的行和列就能表示位置(α,β),例如上图中的玉米片7,(在第1层,旋转0单位,正向,其中认为数字编号在第一列是没有旋转)写成矩阵形式就有:

其中是倒过来的原因是矩阵行数是从上往下的,而拼图中是从下往上的,为了保证数值是一致的所以展现出来是倒过来的。
整体的角标 j 也拆成了三个(s, r, l),其中 s 表示朝向为正(1)或反(2),r 表示旋转的次数(r-1),l 表示所在层数(l)。
使用矩阵后,拼图反向的操作可以通过将矩阵旋转180度(rot90(Y,2))实现(此时层数有一定问题,需要上下平移一定行数);拼图的旋转可以通过矩阵列方向的循环平移(cricshift(A,r-1,2))来实现;而层数直接通过选取矩阵的一部分来实现。
这样在某些层数时有些拼图的一部分可能会超出矩阵(例如上第7块拼图的在超过11层后,如 Y7,(1,1,12) ),这里直接将这一部分丢掉,由于最终要求完全铺满,所以这种丢掉了一部分的状态一定不满足要求,所以不会是最终的解,符合要求。

转换为标准的线性规划问题
这里需要将上述模型转换为matlab能够接受的标准形式:

matlab的混合整数线性规划求解器使用说明
其中变量 x 就是本文的 Pij,只需将 Pij 重新排列(reshape)成一维向量即可,使用第三个等式约束,则需要构造出矩阵 Aeq,beq。
这里略去具体的步骤,仅说明一下这里 Pij 重新排列的顺序依次是:玉米片编号(i),正反向编号(s),旋转编号(r),层数编号(l);Aeq 的每行依次对应的约束是:位置(α,β)处的玉米粒数(顺序不影响结果,程序先排列的行数,共7*14=98行),每个玉米片的状态选择约束(14行),每层只有一个玉米片约束(14行);beq 全为 1。
排列先后顺序意思是前面的序号到达最大后,后面的才会加一(前面的归一),详细的可以参考代码(https://github.com/CHanzyLazer/Yu-Mi)
最终得到 Aeq 的图片还挺好看的(?)

蓝色的点是1,没有的是0
指示所有的变量都为整数,并且上下界为 [0,1],就可以交给matlab来求解了。
结果处理
最后得到的结果可以想象其基本上都是0,然后有几个1,所以还需要用程序统计转换为比较好看懂的结果。
这个步骤就比较简单了,首先先把输出重新排列成以 (i, s, r, l) 为下标的四维数组,直接多重循环遍历,找到为1的下标 (i', s', r', l') ,则第 i' 个拼图的状态就是 (s=s', r=r', l=l'),最终结果写成表格的形式(p_out):
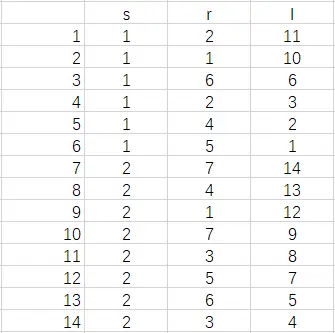
最左侧数字代表玉米片的编号
按照这个编号也可以得到铺满的结果,宣告建模的正确:
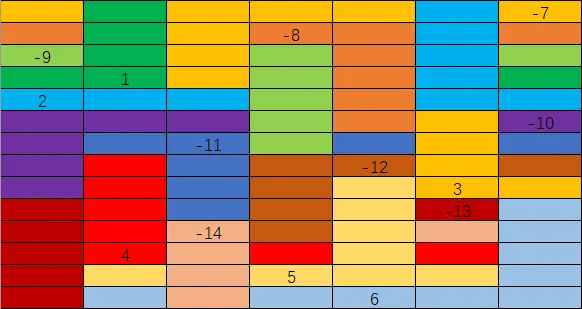
建模计算的结果

GM拼出来的结果
和视频中的结果对比就会发现其实是整体都倒过来了。
总结
这个写成代码后整个运行下来确实在3秒钟之内就能算出来:
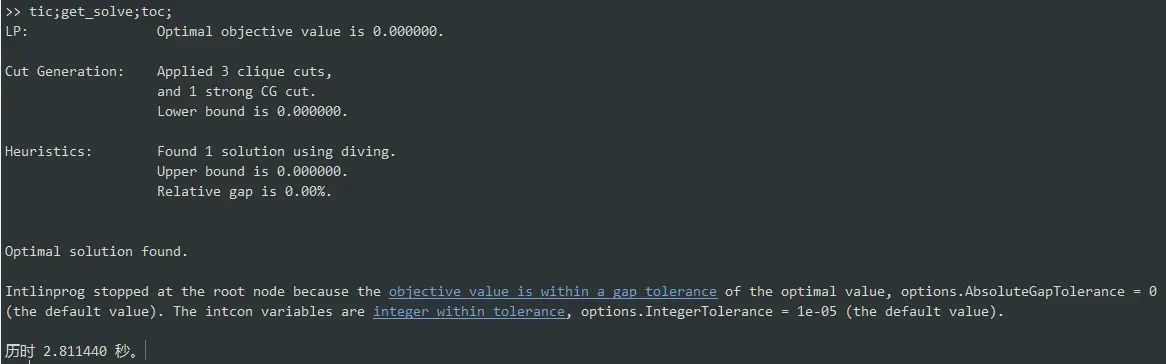
运行结果
不过整个构思加上编程,除去从视频分析玉米片的结构的时间,也不下8个小时了,而且还是我运气比较好,一次性就做对了情况。
当然好处是这种玉米粒类型的拼图都能这样求解出来了,设计师再换种切法那我也能很快算出来。
当然最主要的是通过这个建模的过程我锻炼了我的数学建模能力,复习了数值最优化里的知识点,不过比较遗憾的是整型规划具体操作比较复杂,这里就直接用了matlab现有的求解器了。
代码我上传到github上了(https://github.com/CHanzyLazer/Yu-Mi),感兴趣的可以下载自己运行看看(代码写和github页面都弄的挺随意的)。