一次挺满意的小组合作,记录一下使用的代码和过程。事先声明代码来自chatGPT,由于CSDN上没有找到类似的代码,这也是为以后或许要用到的同学留个资源吧。虽然说代码不是亲自写的,理解还是很容易,顺便注明一些我们走的弯路。

数值方法:
欧拉法:
function [t, y] = euler(f, y0, t0, tf, h)
% Solve an ODE using the Euler method.
% Inputs:
% f: function handle of the ODE
% y0: initial value of y
% t0: initial time
% tf: final time
% h: step size
% Outputs:
% t: array of time values
% y: array of solution values
t = t0:h:tf;
y = zeros(size(t));
y(1) = y0;
for i = 1:length(t)-1
y(i+1) = y(i) + h*f(t(i), y(i));
end很容易理解,顺带提一句chatGPT的代码注释真的很强大。
欧拉法调用方法:
(我们作业内的ODE是,所以下面的都以这个ODE为例,再顺带提一句,使用matlab解ODE用dsolve就好。)
f = @(t,y) 10*y*(1-y);
y0 = 0.01;
t0 = 0;
tf = 1;
h = 0.01;
[t, y] = euler(f, y0, t0, tf, h);
plot(t, y, '-o');
xlabel('t');
ylabel('y(t)');
title('Euler method solution for dy/dt = 10*y*(1-y)');本来想解释一下,但真没啥解释的...定义函数,初值,区间,步长,调用函数,画图,坐标轴和图名,就这些。
欧拉法输出图像:

欧拉法图像
梯形法:
英文是Trapezoidal method,tra pe zo i dal,梯形。
function [t,y] = trapezoidal(f, tspan, y0, h)
% 变量初始化
t0 = tspan(1);
tf = tspan(2);
t = t0:h:tf;
y = zeros(length(y0), length(t));
y(:,1) = y0;
% 梯形法迭代过程
for i = 1:(length(t)-1)
y(:,i+1) = y(:,i) + h/2*(f(t(i), y(:,i)) + f(t(i+1), y(:,i)+h*f(t(i), y(:,i))));
end
end这次tspan是区间,不懂就看下面输入案例。
梯形法调用方法:
f = @(t, y) 10*y*(1-y); % 定义方程
tspan = [0, 1]; % 时间区间
y0 = 0.01; % 初始值
h = 0.01; % 步长
[t,y] = trapezoidal(f, tspan, y0, h); % 调用函数求解
plot(t, y); % 绘制函数图像
xlabel('t');
ylabel('y');
title('Trapezoidal Method');梯形法输出图像:
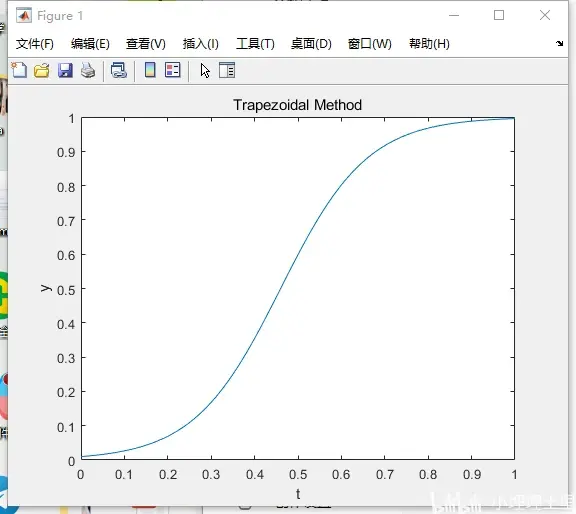
梯形法图像
RK2:
function [t, y] = rk2(f, tspan, y0, h)
% 使用RK2方法求解一阶常微分方程组 dy/dt = f(t, y)
% 输入参数:
% - dydt: 函数句柄,表示方程组 dy/dt = f(t, y) 中的 f(t, y)
% - tspan: 时间区间,形如 [t0, tf]
% - y0: 初始值数组,长度应与输出的 y 数组长度相同
% - h: 步长
% 输出参数:
% - t: 时间数组,包含所有求解点的时间戳
% - y: 解数组,包含所有求解点的值
% 初始化数组
t = tspan(1):h:tspan(2);
n = length(t);
y = zeros(length(y0), n);
y(:, 1) = y0;
for i = 1:n-1
k1 = h * f(t(i), y(:, i));
k2 = h * f(t(i)+h, y(:, i)+k1);
y(:, i+1) = y(:, i) + 0.5 * (k1 + k2);
endRK2调用方法:
f = @(t, y) 10*y*(1-y); % 定义方程
tspan = [0, 1]; % 时间区间
y0 = 0.01; % 初始值
h = 0.01; % 步长
[t,y] = rk2(f, tspan, y0, h); % 调用函数求解
plot(t, y); % 绘制函数图像
xlabel('t');
ylabel('y');
title('Runge-Kutta 2 Method');图不放了,同上(虽然说调用方法也类似,我还是把饼递到嘴边吧)。
RK4:
function [t, y] = rk4(f, tspan, y0, h)
% 变量初始化
t0 = tspan(1);
tf = tspan(2);
t = t0:h:tf;
y = zeros(length(y0), length(t));
y(:,1) = y0;
% 龙格库塔迭代过程
for i = 1:(length(t)-1)
k1 = f(t(i), y(:,i));
k2 = f(t(i)+h/2, y(:,i)+h/2*k1);
k3 = f(t(i)+h/2, y(:,i)+h/2*k2);
k4 = f(t(i)+h, y(:,i)+h*k3);
y(:,i+1) = y(:,i) + h/6*(k1 + 2*k2 + 2*k3 + k4);
end
endRK4调用方法:
f = @(t, y) 10*y*(1-y); % 定义方程
tspan = [0, 1]; % 时间区间
y0 = 0.01; % 初始值
h = 0.01; % 步长
[t,y] = rk4(f, tspan, y0, h); % 调用函数求解
plot(t, y); % 绘制函数图像
xlabel('t');
ylabel('y');
title('Runge-Kutta Method');
误差分析:
我们做的误差分析是得出原函数在t=1时的值和数值方法逼近的值差的绝对值再取对数,听着有点麻烦啊,写成式子应该是这样:。这里我们将步长设为自变量,从10的-1到-6次方,误差为因变量,这样取对数后,正常的误差分析结果应该是几条斜率不同的直线。
代码:
% Defining Differential Equations and Primitive Functions
f = @(t, y) 10*y*(1-y);%ODE方程
y_exact = @(t) 1/(1 + 99*exp(-10*t));%原函数,可以用dsolve求解
% Define step size and interval
h_values = [0.1, 0.01, 0.001, 0.0001, 0.00001, 0.000001];%步长
tspan = [0, 1];%区间
% Initialization
n_values = length(h_values);
error_euler = zeros(n_values, 1);
error_trapezoidal = zeros(n_values, 1);
error_rk4 = zeros(n_values, 1);
error_rk2 = zeros(n_values, 1);
error_exact = zeros(n_values, 1);
% Calculate the error between the Euler method and the original function at t=1
for i = 1:n_values
h = h_values(i);
[t_euler, y_euler] = euler(f, [0.01], 0, 1, h);
y_exact_value = y_exact(1);
error_euler(i) = abs(y_euler(end) - y_exact_value);
error_exact(i) = abs(y_exact_value - y_exact(t_euler(end)));
end
% Calculate the error between the trapezoidal method and the original function at t=1
for i = 1:n_values
h = h_values(i);
[t_trapezoidal, y_trapezoidal] = trapezoidal(f, tspan, [0.01], h);
y_exact_value = y_exact(1);
error_trapezoidal(i) = abs(y_trapezoidal(end) - y_exact_value);
error_exact(i) = abs(y_exact_value - y_exact(t_trapezoidal(end)));
end
% Calculate the error between the RK4 method and the original function at t=1
for i = 1:n_values
h = h_values(i);
[t_rk4, y_rk4] = rk4(f, tspan, [0.01], h);
y_exact_value = y_exact(1);
error_rk4(i) = abs(y_rk4(end) - y_exact_value);
error_exact(i) = abs(y_exact_value - y_exact(t_rk4(end)));
end
% Calculate the error between the RK2 method and the original function at t=1
for i = 1:n_values
h = h_values(i);
[t_rk2, y_rk2] = rk2(f, tspan, [0.01], h);
y_exact_value = y_exact(1);
error_rk2(i) = abs(y_rk2(end) - y_exact_value);
error_exact(i) = abs(y_exact_value - y_exact(t_rk2(end)));
end
% Draw error image
log_h_values = log10(h_values);
log_error_euler = log10(error_euler);
log_error_rk4 = log10(error_rk4);
log_error_trapezoidal = log10(error_trapezoidal);
log_error_rk2 = log10(error_rk2);
log_error_exact = log10(error_exact);
plot(log_h_values, log_error_rk2, 'o-', log_h_values, log_error_euler, 's-', log_h_values, log_error_rk4, 'x-', log_h_values, log_error_trapezoidal, '+-');
set(gca,'XDir','reverse'); %Set the x-axis direction to reverse
xlabel('log(h)');
ylabel('log(error)');
title('Error image');
legend('RK2', 'Euler','RK4','Trapezoidal');误差分析图像:

误差分析图像
小问答:这里直线的斜率分别为1,2,4,原因是什么?
另外,效果最好的是RK4,我一开始疑惑为什么RK4方法会触底反弹,chatGPT的解释是:
使用RK4方法拟合函数时,有时在步长减小到一个值时,随着步长继续减小,误差反而增大的原因:在RK4方法中,步长的大小会影响拟合精度,通常情况下,减小步长可以提升拟合的精度。然而,当步长继续减小时,误差反而增大的原因在于舍入误差的影响。由于计算机存储浮点数是有限精度的,当步长较小时,函数的微小变化可能会因为精度不足而被忽略,从而导致误差逐渐累积,最终使得计算结果和真实结果之间的差距增大。
我也询问了为什么欧拉法和RK2为什么不会如此,chatGPT解释是:
欧拉法和RK2方法在同样的函数上进行数值积分时,没有出现这种问题的原因是因为它们的计算精度相对较低,误差随着步长的减小而不是增大。欧拉法和RK2方法都是数值积分常用的一阶显式方法,与RK4方法相比,它们的计算复杂度较低,每次迭代只需要使用一次函数导数计算即可。这种简单的计算方式使得它们在处理简单的函数时更加高效。然而,这种高效性也带来了精度的牺牲。相较于RK4方法的四阶精度,欧拉法只有一阶,而RK2方法只有二阶。因此,在进行数值积分时,它们的误差通常较大。
一些踩坑:
之后,我们换了一个新的函数,区间设为0到60。我们一开始想用函数中间的值来对比误差,即y(30),结果搞出一个四不像图像,具体的就不放了。后来在做报告前,我们才发现在误差分析的代码中,我们用了例如y_exact(t_euler(end))的函数。我们将步长,初值,区间和取值全都换为了新的函数,但就是没发现这个...最后作差是将函数中间数值方法的值和原函数末端值比较,当然完全不对了。还是没有完全理解如此简单的代码啊。顺带一提这些迭代的方法,比较函数末端(end)值其实应该是最能显示误差的。
最后看看我们对另一个函数做的误差分析图吧:

f = @(t, y) -0.051*(y-24);
注意两个误差分析图的斜率哦!