
起因是看到这个动画,up主贴心地附上了代码(不知道是什么语言的),心里痒痒,花了好几个小时用Matlab实现了这些效果,
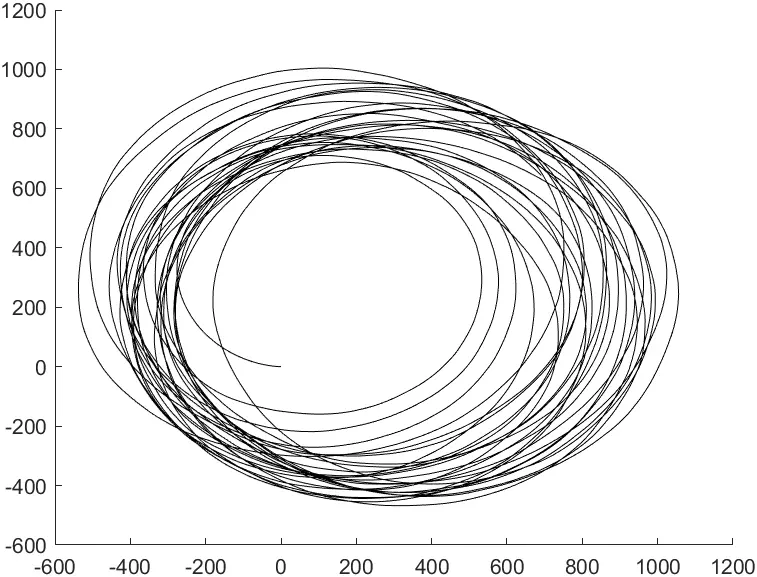
空洞的瞳孔(旋转角度359°)
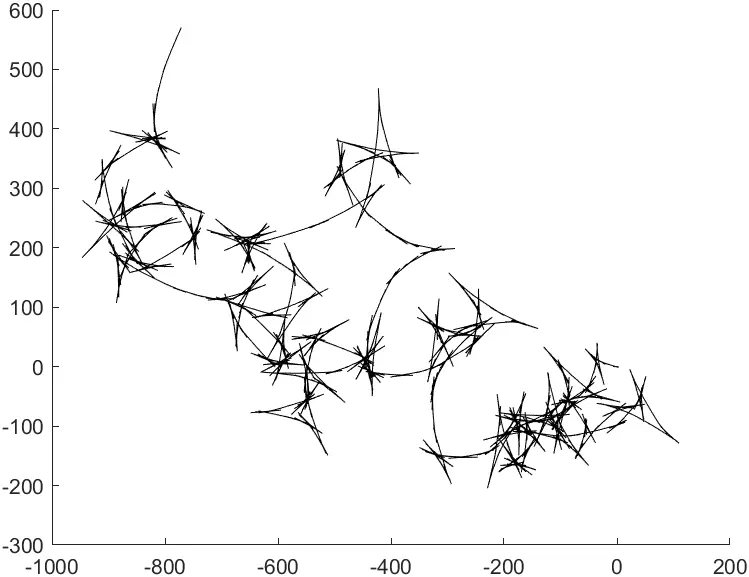
荆棘丛外的少女(旋转角度179.5°)
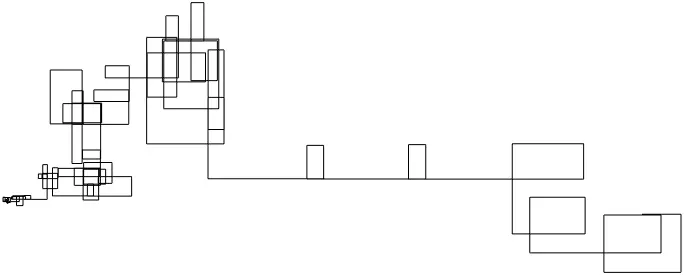
前进速度不是1,而是当前数字
下面是代码的三个主要版本(B站专栏代码块没有matlab选项,就选了C),省略了一些不怎么样的尝试。

获取点坐标
检索素数的工作可以交给Matlab自带函数primes,省了很多时间。
k=-2和k=k-1是为了和原视频保持一致。
clear;clc;close all %清空之前的数据
n = 10^5;%点的数量
p = primes(n);%n以内的素数列表
A = zeros(n,2);%用于储存所有的点坐标,zeros是为了预先分配好内存
k = -2;%素数个数,同时用于决定方向,初始值决定起始方向
for m = 2:n %从2开始,1在原点
if ismember(m,p)
k = k-1;%-1控制向左转,+1控制向右转
end
if mod(k,2)==0 %k为偶数时
A(m,1) = A(m-1,1)+(-1)^(k/2);%横坐标±1
A(m,2) = A(m-1,2);%纵坐标不变
else %k为奇数时
A(m,1) = A(m-1,1);%横坐标不变
A(m,2) = A(m-1,2)+(-1)^((k-1)/2);%纵坐标±1
end
%在此处addpoints会降低运行效率
end注:后面两个版本省略部分代码。
后来发现判断k的奇偶性的代码可读性较差,而且仅仅是旋转90°,想把它扩展为任意角度,而且旋转和复数关系紧密,于是用欧拉公式和复数乘法实现了可以调节角度,也就是修改下面的第二行代码。
z = -1;%复数z决定前进方向,初始值决定起始方向
w = exp(1/4*pi*1i); %复数w决定旋转角度
for m = 2:n %从2开始,1在原点
if ismember(m,p)
z = z*w;
end
A(m,1) = A(m-1,1)+real(z);
A(m,2) = A(m-1,2)+imag(z);
end但我惊讶地发现这两个版本的运行效率没有显著区别(相差1%左右),用“运行并计时”和探查器功能发现主要花在ismember函数上。于是有了第三个版本。
在循环外使用ismember函数,得到由0和1组成的is_prime列表,0代表自然数列表N中对应的自然数为合数,1代表素数。
N = [1:n];%自然数列表
is_prime = ismember(N,p);
for m = 2:n %从2开始,1在原点
if is_prime(m) == 1
z = z*w;
end
A(m,1) = A(m-1,1)+real(z);
A(m,2) = A(m-1,2)+imag(z);
end对比一下两张探查器截图,可以看出节省了接近95%的时间。
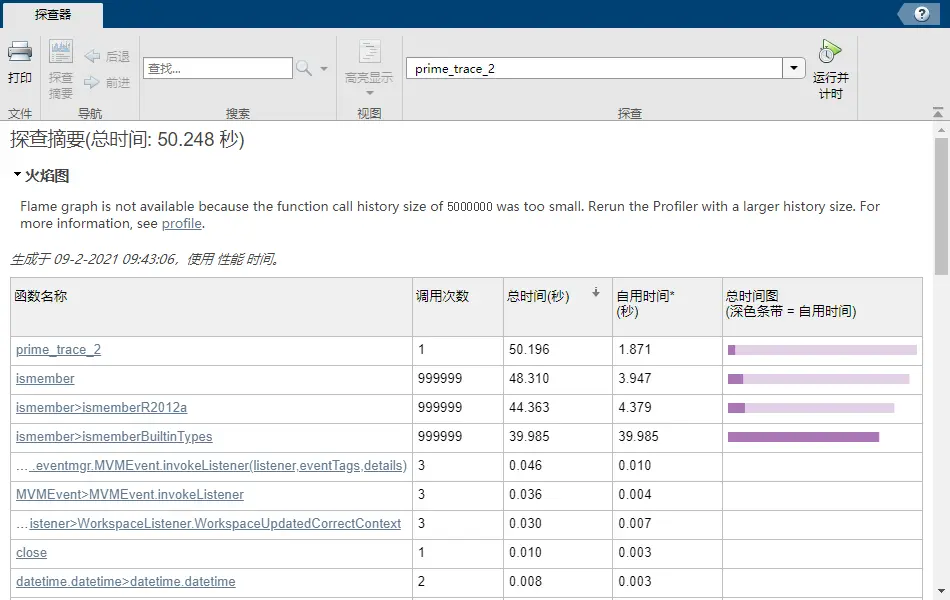
n=10^6时,第二版ismember函数占了96%的时间。
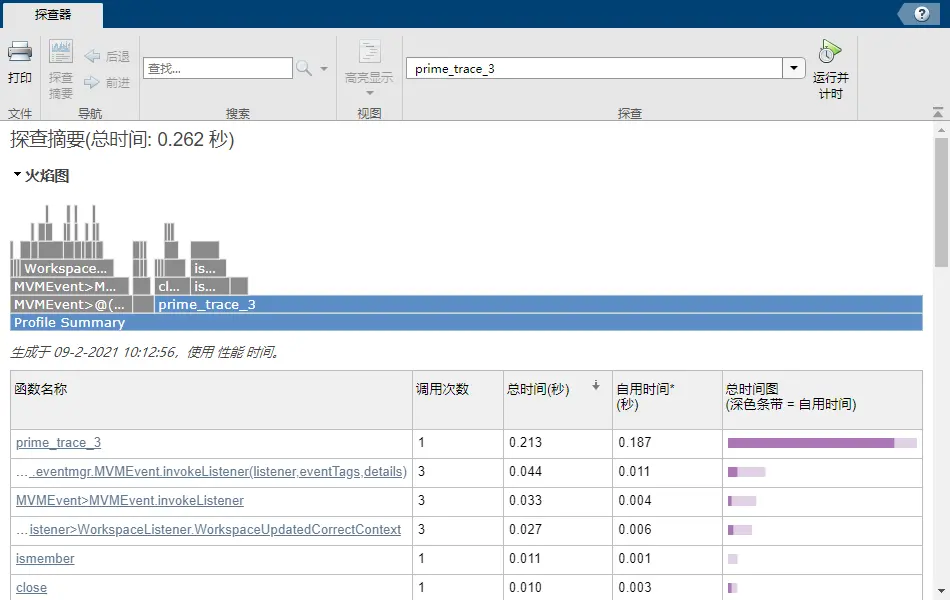
n=10^6时,第三版耗时仅有第二版的5%

制作线条动画
在获得所有点坐标后就可以开始制作线条动画。
l = animatedline;%线条动画
for i = 1:n
addpoints(l,A(i,1),A(i,2)) %从矩阵A中依次逐个读取每个坐标
drawnow limitrate %加速绘制
endlimitrate能够加速动画,其他控制动画速度的方式参考Matlab官方文档。如果不想要线条动画,只想要最后的绘制结果,可以把drawnow放在循环外面。
用参数MaximumNumPoints可以控制同时出现在坐标系上的点的数量,也就是控制线条的长度,看上去很像贪吃蛇。比如下面的代码就是可控制在1000个点。
l = animatedline('MaximumNumPoints',1000)

扩展性
旋转角度的另一种表示
angle = 90; %旋转角度
w = exp(angle/180*pi*1i);增加调节前进速度的功能
speed = m;%前进速度
A(m,1) = A(m-1,1)+speed*real(z);
A(m,2) = A(m-1,2)+speed*imag(z);显示网格线或去除坐标轴
axis equal;%使x、y轴单位长度一致
axis off;%隐藏坐标轴
grid on;%显示网格线(需要axis on)
遗留问题
作为Matlab小白,做这个项目的过程虽有磕磕碰碰,但总体难度不高,而扩展性较强,多查查官方文档和搜索引擎就可以完成,推荐和我一样的Matlab新手练习这个项目,也欢迎大家讨论~
注:文中代码开源。