软件
产品
import pandas as pdimport tensorflow as tfimport numpy as npfrom matplotlib import pyplot as pltplt
.rcParams['font.sans-serif']=['SimHei'] #显示中文标签plt.rcParams['axes.unicode_minus']=False
#解决负号“-”显示为方块的问题data=pd.read_csv('D:/code/python/pythonProject/tensorflow51自学/
tensorflow入门与实战-基础部分数据集/Income1.csv')x=data.Educationy=data.Incomemodel=tf.keras
.Sequential()#定义模型, 使用一层全连接, 输出为一维,输入为一维model.add(tf.keras.layers.Dense(1,input_shape=(1,)))
#编译模型, 使用adam(梯度下降)作为优化函数, 使用mse(均方差)作为损失函数model.compile(optimizer='adam',loss='mse')
#mes均方差# 开始训练history=model.fit(x,y,epochs=50000)#训练次数# Y=model.predict(pd.Series([20]))
#使用训练后的模型进行预测Y=model.predict(x)plt.plot(x,Y,'r-s',label="训练模型预测")plt
.scatter(data.Education ,data.Income,color='b',label='原始数据')#一元线性b=np
.sum((x-np.mean(x))*(y-np.mean(y)))/np.sum((x-np.mean(x))**2)a=np.mean(y)-b*np
.mean(x)x1=np.arange(10,22)y2=b*x1+aplt.plot(x1,y2,'m-p',label='一元线性预测')plt
.legend()plt.show()1.2.3.4.5.6.7.8.9.10.11.12.13.14.15.16.17.18.19.20.21.22.23.24.25.26.27.28.29.Income1.csv数据,其中Education为受到教育年限、Income为收入,想预测受到教育的年限和收入之间的关系
| Education | Income |
| 10 | 26.65884 |
| 10.40134 | 27.30644 |
| 10.84281 | 22.13241 |
| 11.24415 | 21.16984 |
| 11.64548 | 15.19263 |
| 12.08696 | 26.39895 |
| 12.48829 | 17.43531 |
| 12.88963 | 25.50789 |
| 13.29097 | 36.88459 |
| 13.73244 | 39.66611 |
| 14.13378 | 34.39628 |
| 14.53512 | 41.49799 |
| 14.97659 | 44.98157 |
| 15.37793 | 47.0396 |
| 15.77926 | 48.25258 |
| 16.22074 | 57.03425 |
| 16.62207 | 51.49092 |
| 17.02341 | 61.33662 |
| 17.46488 | 57.58199 |
| 17.86622 | 68.55371 |
| 18.26756 | 64.31093 |
| 18.70903 | 68.95901 |
| 19.11037 | 74.61464 |
| 19.51171 | 71.8672 |
| 19.91304 | 76.09814 |
| 20.35452 | 75.77522 |
| 20.75585 | 72.48606 |
| 21.15719 | 77.35502 |
| 21.59866 | 72.11879 |
| 22 | 80.26057 |
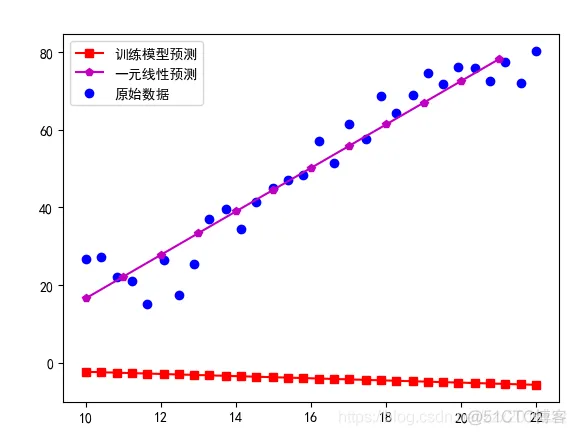
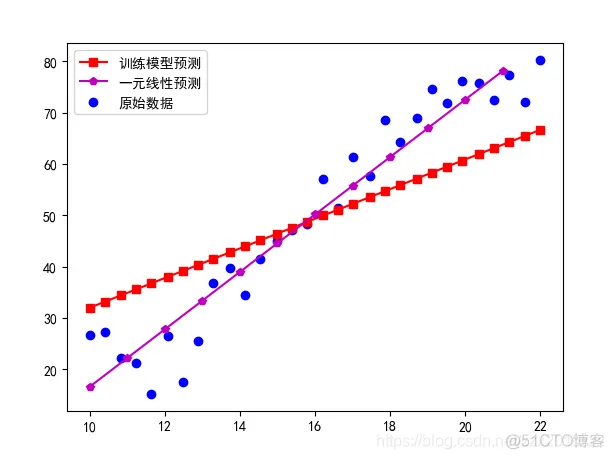
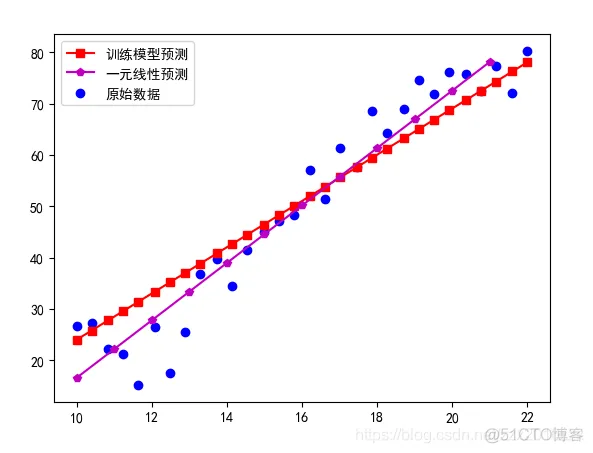
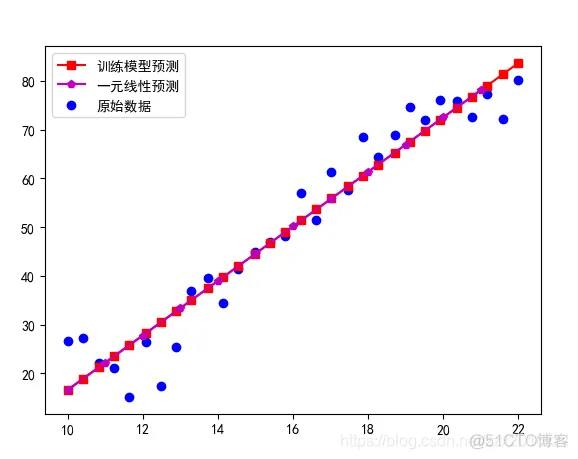
总结:随着模型训练次数的增加,训练的一元线性回归越来越接近标准的线性回归模型,从中可以看出,只要训练次数足够大,训练模型就可以无线逼近直到完成和标准的模型重合
免责声明:本文系网络转载或改编,未找到原创作者,版权归原作者所有。如涉及版权,请联系删