智能算法在电力系统最优规划中的Matlab仿真应用

1.软件版本

matlab2013b

2.本算法理论知识

在一个中长期电网规划中，需要考虑的目标函数可以认为是新建电网线路的投资年费用和电网系统的运行费用之和的最小值，满足这目标值最小且符合电网运行的约束要求即是求解问题的最优解。根据这个原理，首先给出任意一年的目标函数为：

        公式中，

表示的是新建线路的集合；

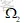
表示的是所有线路的集合；W表示的是总的规划费用；

表示的是资金回收系数；

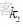
表示的是工程固定运行费率；

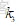
表示的是线路网损费用系数；

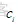
表示的是电网支路i扩展一条新的线路的费用；

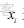
表示的是电网支路i扩展一条新的线路数量；

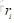
表示的是支路i的电阻；

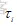
表示的是支路i的电能年损耗小时数；

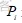
表示的是正常运行情况下支路 i 的输送的有功功率。

        而在一个中长期电网规划中，需要考虑每一年的成本，那么电网规划总成本由新建线路总成本以及历年运行费用之和，那么公式中的目标函数可以改写为：

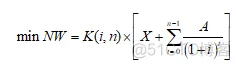
       公式3.3中，X表示的是整个新建线路的总成本，相当于公式3.1的第一项；

表示的是电网系统第一年的运行成本，相当于公式3.2的第二项；i表示贴现率；K为资金收回系数系数，其可以通过

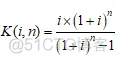
计算得到。那么中长期电网规划的优化目标函数可以定义为：

3.部分核心代码

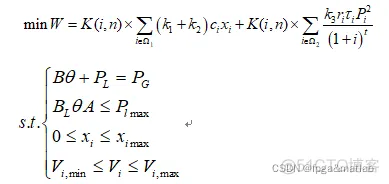
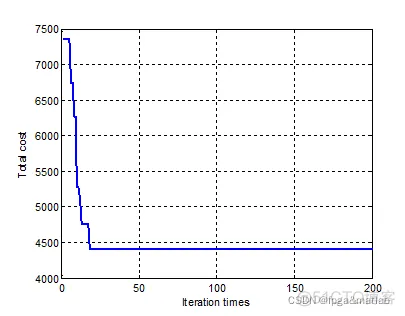
clc;clear;close all;warning off;addpath 'func\'addpath 'GA_toolbox\'rng(1);%编号NO    = [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15]';%线路首端号START = [1,1,1,1,1,2,2,2,2,3,3,3,4,4,5]';%线路末端号ENDS  = [2,3,4,5,6,3,4,5,6,4,5,6,5,6,6]';%支路电抗ZDK   = [40,50,60,20,10,20,20,40,20,20,30,48,30,20,10]';%容量限制Vmax  = [100,100,80,100,70,100,100,100,100,82,100,100,75,100,78]';%线路长度Len   = [40,38,60,20,68,20,40,31,30,59,20,48,63,30,61]';%电抗DZ    = [0.1,0.09,0.15,0.05,0.17,0.05,0.1,0.08,0.08,0.15,0.05,0.12,0.16,0.08,0.15]';%电抗DK    = [0.4,0.38,0.6,0.2,0.68,0.2,0.4,0.31,0.3,0.59,0.2,0.48,0.63,0.3,0.61]';tmps  =[NO,START,ENDS,ZDK,Vmax,Len,DZ,DK]; %整理IEEE6 =[tmps([1,3,4,6,7,11],:);tmps([9,11,14],:)]; %初始线路Nline =[1,1,1,1,1,1,0,0,0];   %初始邻接矩阵Connect=[0 1 0 1 1 0;         1 0 1 1 0 0;         0 1 0 0 1 0;         1 1 0 0 0 0;         1 0 1 0 0 0;         0 0 0 0 0 0];%各节点注入功率P = [-30,-240,125,-160,-240]';             %节点数 N = 6;     tic;%定义遗传算法参数%种群规模NIND   = 1000;                                                                %迭代次数MAXGEN = 200;                                                                                                             Price  = zeros(MAXGEN,1);          %基向量 BaseV  = 5*ones(1,length(Nline));Chrom  = crtbp(20,BaseV); gen    = 0;   %初始种群函数值ObjV   = func_obj(Chrom,IEEE6,Nline,Connect,P,N); df     = 1000;while gen< MAXGEN      gen      if gen == 0         Pe = 0.92;       else         Pe = 1/(1+exp(-df/10));        end      gen   = gen+1;      FitnV = ranking(ObjV);                 %选择      SelCh = select('sus',Chrom,FitnV);                                    SelCh = recombin('xovmp',SelCh,Pe);        %重组      f     = [zeros(1,length(Nline));5*ones(1,length(Nline))];            %变异      SelCh        = mutbga(SelCh,f);                                                     SelCh        = fix(SelCh);         ObjV2        = func_obj(SelCh,IEEE6,Nline,Connect,P,N);                                            [Chrom,ObjV] = reins(Chrom,SelCh,1,1,ObjV,ObjV2);       indx         = find(isnan(ObjV) == 1);      ObjV3        = ObjV;      ObjV3(indx)  = [];      Price(gen)   = min(ObjV3);        if gen > 1         df        = abs(Price(gen) - Price(gen-1));      endend[Y,I]   = min(ObjV);                        %规划Net_new = Chrom(I,:);Net_newY   figure;plot(Price,'b','linewidth',2);grid on    xlabel('Iteration times');ylabel('Total cost');toc; save R2.mat Price1.2.3.4.5.6.7.8.9.10.11.12.13.14.15.16.17.18.19.20.21.22.23.24.25.26.27.28.29.30.31.32.33.34.35.36.37.38.39.40.41.42.43.44.45.46.47.48.49.50.51.52.53.54.55.56.57.58.59.60.61.62.63.64.65.66.67.68.69.70.71.72.73.74.75.76.77.78.79.80.81.82.83.84.85.86.87.88.89.90.91.92.93.94.95.96.97.98.99.100.101.

4.仿真结论

免责声明：本文系网络转载或改编，未找到原创作者，版权归原作者所有。如涉及版权，请联系删