Pro/ENGINEER（Creo）曲面造型设计的专业技巧

1.1曲面设计发展：

1、曲面造型（surface modeling）：计算机技术与数学方法的结合发展产物，是计算机辅助几何设计（computer aided geometric design）和计算机图形学（computer graphics）的一项重要内容

2、研究内容:在计算机图像系统的环境下，对曲面的表达、创建、显示以及分析等

3、发展历史：

(1) 1963年，波音公司，参数的矢量函数方法，参数三次曲线；曲线曲面的参数化形式成为形状数学描述的标准形式

(2) 1971年，雷诺公司，控制多边形设计曲线，解决整体形状控制问题

(3) 1975年，美国Syracuse大学，有理B样条（NURBS）方法，使用统一的数学形式精确表示规则曲线曲面

4、目前发展：

(1) 研究领域：从传统研究曲面表示、曲面求教拼接等到曲面变形、重建、转换、等距等

(2) 表示方法：网格细分为特征的离散造型方法，优势：特征动画、雕塑曲面

(3) 造型方法：基于物理模型、偏微分方程的曲面造型方法、流曲线曲面造型方法等

5、Creo：参数化，基于特征、全相关等，特殊曲面建库导入

1.2曲面造型的数学概念

曲面造型实际是数学方法在计算机上的图像辅助设计呈现

1、贝塞尔（bezier）曲线与曲面

法国雷诺1962年提出，是三次曲线的形成原理，由四个位置矢量Q0、Q1、Q2、Q3定义的曲线，bezier控制多边形：Q0、Q1、Q2...Qn组成的多边形，第一和左后一条为切线，其他定义曲线阶次与形状

2、B样条曲线与曲面

拥有贝塞尔（bezier）曲线优点，易修改，易推广至曲面，与特征多边形十分接近

3、非均匀有理B样条（NURBS）曲线与曲面

Non-Uniform Rational B-Splines

(1) Non-Uniform（非统一）：控制点影响力范围可改变

(2) Rational（有理）：指每个NURBS物体都可用数学表达式定义，

该技术提供对标准几何和自由曲面、曲线的统一数学描述方法，通过控制顶点和因子，改变曲面形状，为主流表示方法

4、NURBS曲面的特性及曲面连续性定义

(1) 用数学方法描述形体，每个都有对应坐标（x，y，z），具有高度的精确性，曲面可由任何曲线生成，剪切不会对曲面的UV方向（类似地球经纬线）产生影响（曲面）

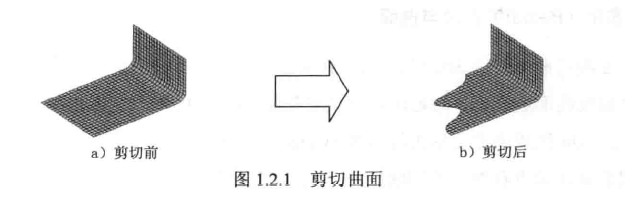
(2) 曲面G1与G2连续性定义：Gn表示两个几何对象间的实际连续程度

G0：两个对象光滑连接，一阶微分连续，或者是相切连续的。

G1：两个对象光滑连接，二阶微分连续，或者两个对象的曲率是连续的（曲率连接约束）。

G2：两个对象光滑连接，三阶微分连续。（高数曲面连续条件）

1.3 曲面造型方法

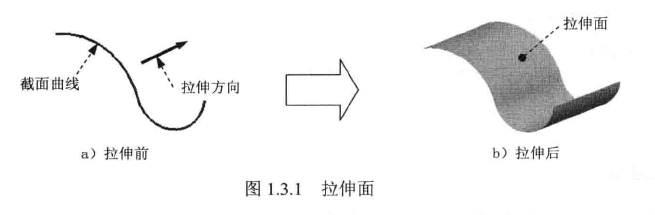
1、拉伸面：由一条曲线光滑平移所形成的曲面

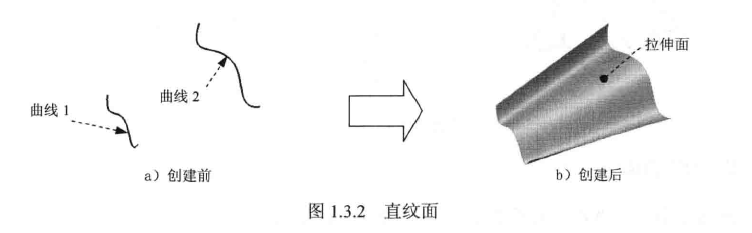
2、直纹面：两条形状相似且节点数相同，对应点用直线相连；另外两条曲线走向必须相同，否则出现扭曲（边界混合放样）

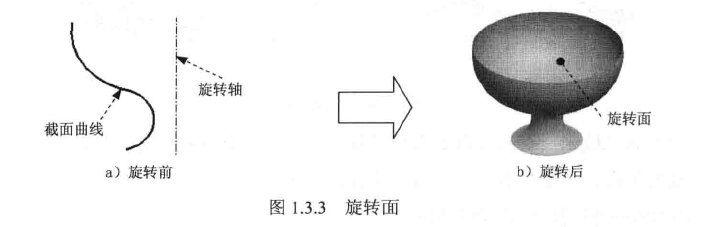
3、旋转面：一条曲线（可封闭可开端）绕一中线轴旋转一定角度

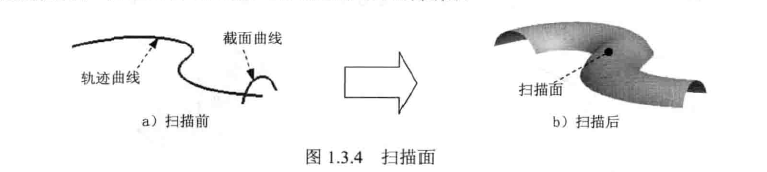
4、扫描面：将截面曲线（可多条，可封闭可开端）沿着轨迹线（可多条）扫描

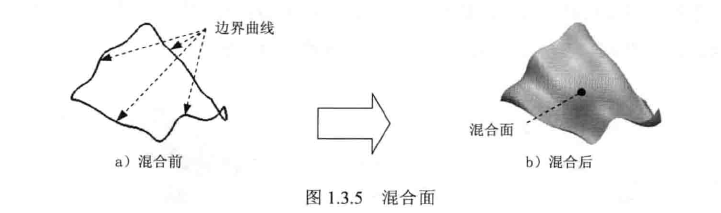
5、混合面：以一系列曲线为骨架进行形状控制，自然过渡

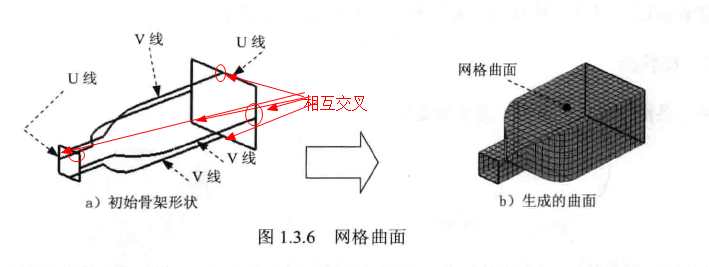
6、网格曲面：两组UV线相互交叉、形成一张网格骨架的截面曲线上生成的曲面；先构造UV线（变截面扫描）；UV线各自不能相互交叉，否则不能成型

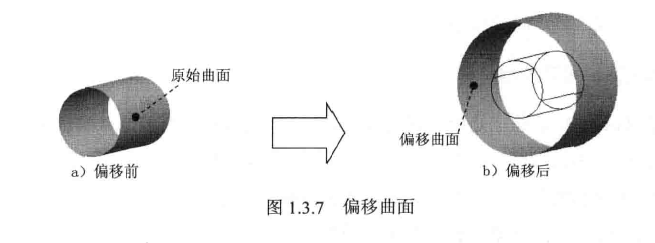
7、偏移曲面：将曲面特征沿某个方向偏移一定距离

1.4 光滑曲面造型技巧

理论：二阶几何连续、不存在奇点和多余拐点、曲率变化较小

1、区域划分，先局部再整体

根据零件曲面特征划分曲面，逐个画出再进行合并；尽量将每个子面划分成四边形区域，即拥有四条边，出现三边形可由四边形构造再成型或用四边形剪切再成型

2、创建光滑的控制曲线是关键

曲线的光滑程度决定曲面质量：

(1) 要达到精度的要求；

(2) 曲率方向要尽可能一致（曲率图不突变）；

(3) 曲率要大于圆角过渡的半径值（否则圆角过渡失去意义）

创建步骤上：利用投影、插补、光滑等手段生成样条曲线，根据曲率图控制节点调整（交互式曲线修改）

3、光滑连接曲面片

条件：

(1) 具有公共边

(2) 各曲面控制线连接光滑，调节连接处约束条件（曲率、垂直、相切、自由连接）

4、还原曲面，再塑轮廓

由投影二维轮廓线建立曲面，再利用曲面相交生成三维曲线轮廓，利用轮廓再构建其他曲面

5、注重实际，从模具的角度考察曲面质量

产品三维造型的最终目的是制造模具。考虑模具制造工艺。

6、随时检查，及时修改（查看曲面质量：G0、G1、G2）

检查方法：

(1) 渲染处理：透视、透明度、多重光源等进行逼真观察，根据阴影反射等进行观察，明暗度变化均匀

(2) 高斯曲率分析：彩色光栅图像，颜色变化区域大均匀不突变（G2），颜色过渡区域小变化快（G1），颜色变化没有过渡、有棱边（G0）

(3) 斑马线：反射条纹连续不中断且无突然转向，转向光滑，属于G2质量；连续有转向属于G1；不连续属于G0。

(4) 偏移：检查最大能够偏移多大，是否最后有收敛点（曲率颜色集中）。

免责声明：本文系网络转载或改编，未找到原创作者，版权归原作者所有。如涉及版权，请联系删