MATLAB脚本实战：从wannier90_hr文件提取哈密顿量

Wannier90是一款强大的开源代码，可以生成局域wannier函数，并使用它们来高效精确地计算材料的电子性质。通过wannier90，我们可以获取基于wannier function basis的哈密顿量矩阵，并将其利用于紧束缚模型近似的计算当中。但是程序默认输出的文件内容比较庞大，可以通过设计一些简单的程序帮助我们筛选想要获取的重要信息。这里，本文将使用MATALB脚本（要求版本号大于R2019a）来提取指定多个格点的全部哈密顿量，并将它们各自保存成表格形式，大大方便了数据的处理过程。

先贴出代码(因为目前B站代码块没有对应matlab规则，所以高亮看起来很乱)：

clc;clear;
[filename, pathname] = uigetfile('*.dat','Please select wannier90_hr.dat');
pathfile=fullfile(pathname, filename);  % Obtain file location
S = importdata(pathfile);
Data = S.data;
Nw = Data(1);Data(1) = [];
Nrpts = Data(1);Data(1) = [];
Ndegen = Data(1:Nrpts)';Data(1:Nrpts)=[];
H = reshape(Data,7,[])';

Direct = [0 0 0; 0 0 1; 1 0 0; 0 1 0; 1 0 1; 1 1 0; 0 0 2]; %Obtain the hopping term on site (l,m,n) as you want

for i = 1:length(Direct(:,1))
    l=Direct(i,1);m=Direct(i,2);n=Direct(i,3);
    temp= find(H(:,1)==l & H(:,2)==m & H(:,3)==n);
    Htemp= H(min(temp):max(temp),:);
    Htemp(:,6:7)=Htemp(:,6:7)/Ndegen(max(temp)/Nw^2);
    Hmat = reshape(Htemp(:,6),Nw,[]); %replace 6 with 7 to output Im(H)
    name = [pathname,num2str([l m n]),'.xlsx']; %Modify '.xlsx' to change the format of output
    writematrix(Hmat,name,'WriteMode','replacefile','UseExcel',true);
    %If you are not going to output in spreadsheet,
    %remember to remove comma-separated pair 'UseExcel',true
end

整个代码里需要手动改的只有一项就是Direct矩阵，它是以3*n的形式保存的。若你想输出格点(l,m,n)的哈密顿量，就请把l,m,n以一行的形式写入到Direct里，要输出多个格点就继续增加更多的行。

接下来我们以钙钛矿结构的SrVO3（SVO）为例来具体展示下程序的使用方法。(例子中用到的文件 

链接：https://pan.baidu.com/s/16B4q5K07T_2tIvMsVvnC_A 

提取码：ks3s )

通过DFT求得块体SVO的部分能带如下图所示

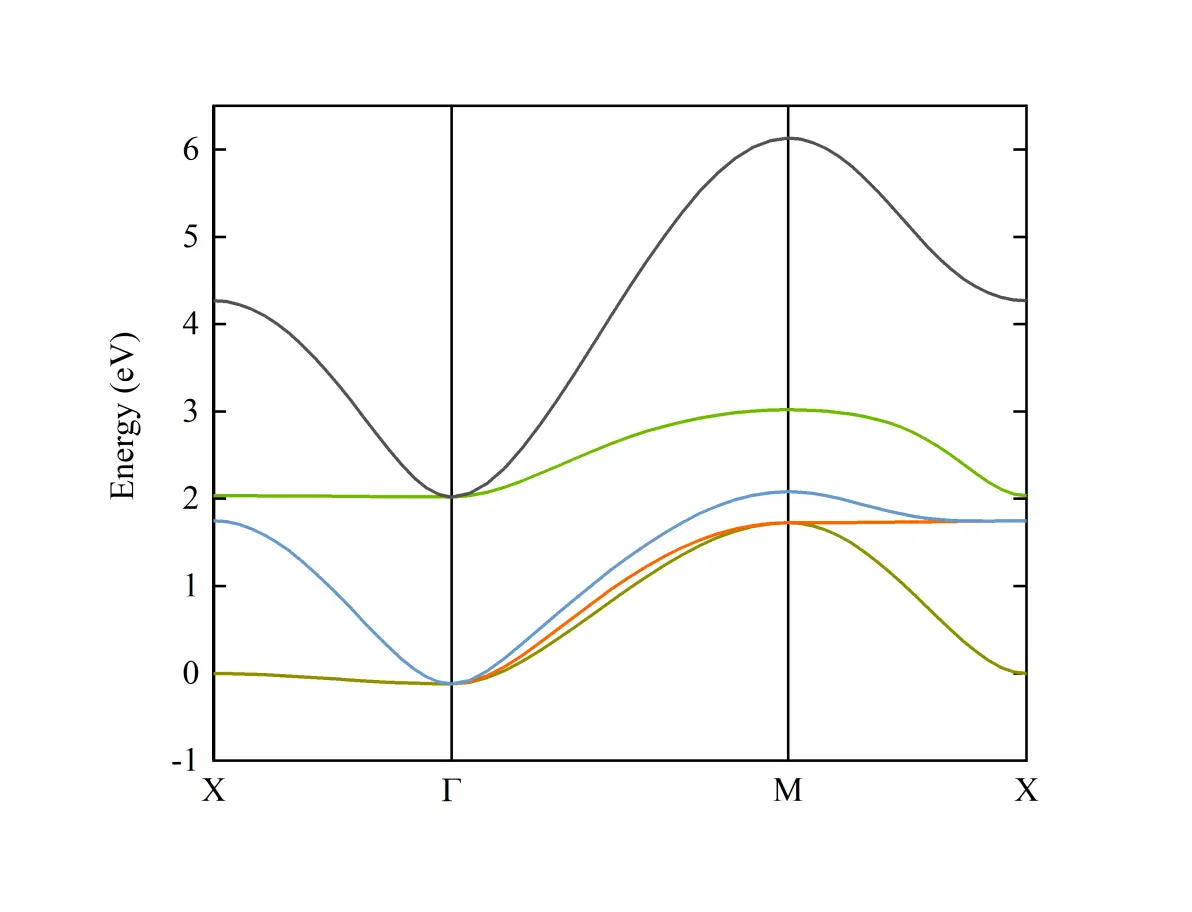
SVO V 3d轨道能带

SVO中V原子的3d轨道能带分布在[0, 6]eV范围内，且与其他轨道没有杂化，非常适合用于做wannier projection。选取V的3d轨道Wannier Function作为Basis，求得wannier90_hr.dat，这一步的具体过程可以参考下站内的一个教程。

建议将wannier90_hr.dat单独保存在一个文件夹内，然后运行程序，此时会弹出一个文件选择界面，选择想要处理的文件并确认。

之后，程序会自动根据你输入的Direct输出对应的哈密顿量并保存为表格形式（表格会根据格点矢量自动命名，并保存在和.dat一个目录下）。如果想保存成文本格式，可以在第19行修改后缀名为'.txt'，并移除第20行的最后一个逗号分割对。(PS:如果你很想输出虚部的结果，可以把第18行的6改为7)

简单介绍下下输出的矩阵形式到底是怎样的，以(0,0,0)为例

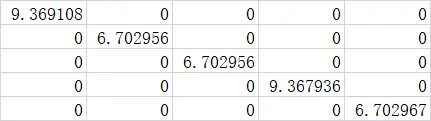
hopping term (0,0,0)

wannier的输出顺序为，l相同时依次输出m=0,±1,±2,...,±l的线性组合。在本文的这个案例中V的3d轨道电子l=2，矩阵从左至右，从上到下每个对应的轨道分别是dz2(m=0),dxz,dyz(m=±1),dx2-y2,dxy(m=±2)。可以看出各轨道电子的格点能是正交化的，且分别对应三重和二重简并的t2g和eg轨道。

接下来这一部分简单谈一下结果分析的部分，有些部分的数学和物理证明会被掠过，如果不太熟悉的朋友可以回头再看一下紧束缚近似的理论。

在这个例子中分析所有的hopping terms，我们可以发现两个关于它们的鲜明特性：

1. 所有的不同轨道间hopping terms都是0或者小到可以被忽略，比如(0,0,0)和(0,0,1)都是正好等于0，比如(1,1,0)和(0,0,2)它们的就非常小。因此，不同轨道之间的hopping在近似的过程中可以被忽略掉，在处理的过程中可以把它们看作相互独立的。
2. 不论是沿着哪个方向，次近邻的hopping terms都是非常小的，因此在描述块体SVO的能带的时候是只需要考虑到近邻项即可。

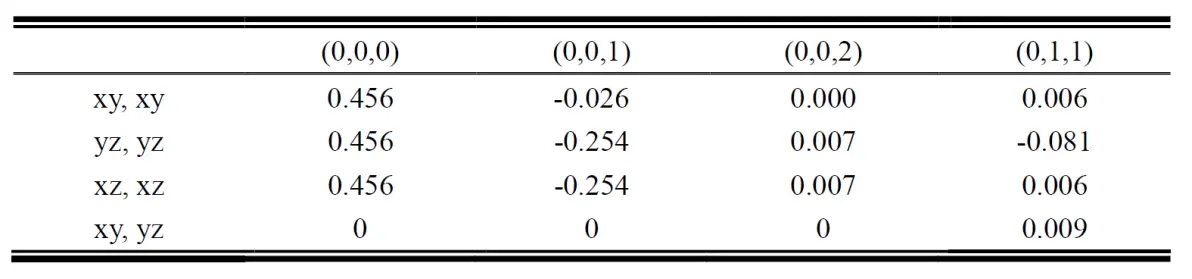
Table I : Hopping integrals in SVO bulk, (0,0,0) have been substracted by fermi energy 6.2472 eV 

因此，结合SVO的晶格对称性(cubic)，对于每个轨道α沿着特定方向比如z，哈密顿量可以简化为

接下来求哈密顿量中的两个常数ε和t，例如xy轨道沿着z方向，另外根据对称性可得主要的hopping terms 只有四种（建议仔细观察下各个格点的hopping terms，重复的值很多）：t0=(0,0,0)=0.456 eV, t1=(1,0,0)=-0.254 eV，t2=(0,0,1)=-0.026 eV, t3=(1,1,0)=-0.081。各自的ε和t分别为

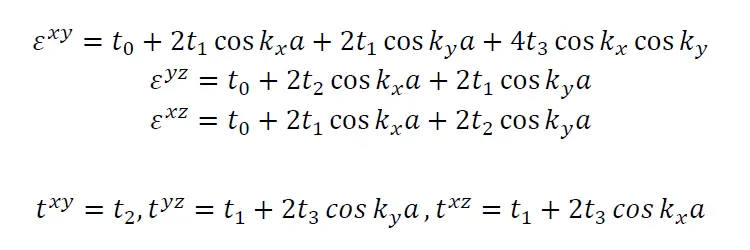
各轨道ε和t的表达式

现在我们来关注从Γ(0,0,0)点到X(0,0,pi/a)点的能带色散，yz轨道X点的能量等于tyz+εyz=(t1+2*t3)+(t0+2*t1+2*t2)=-0.416-0.114=-0.53eV。xz轨道由于对称性的原因和yz轨道的能量在这个点上简并。xy的能量等于txy+εxy=t2+t0+4t1+4t3=-0.91eV。而在Γ点，三个t2g轨道的能量是简并的，大小都等于t0+4t1+2t2+4t3。

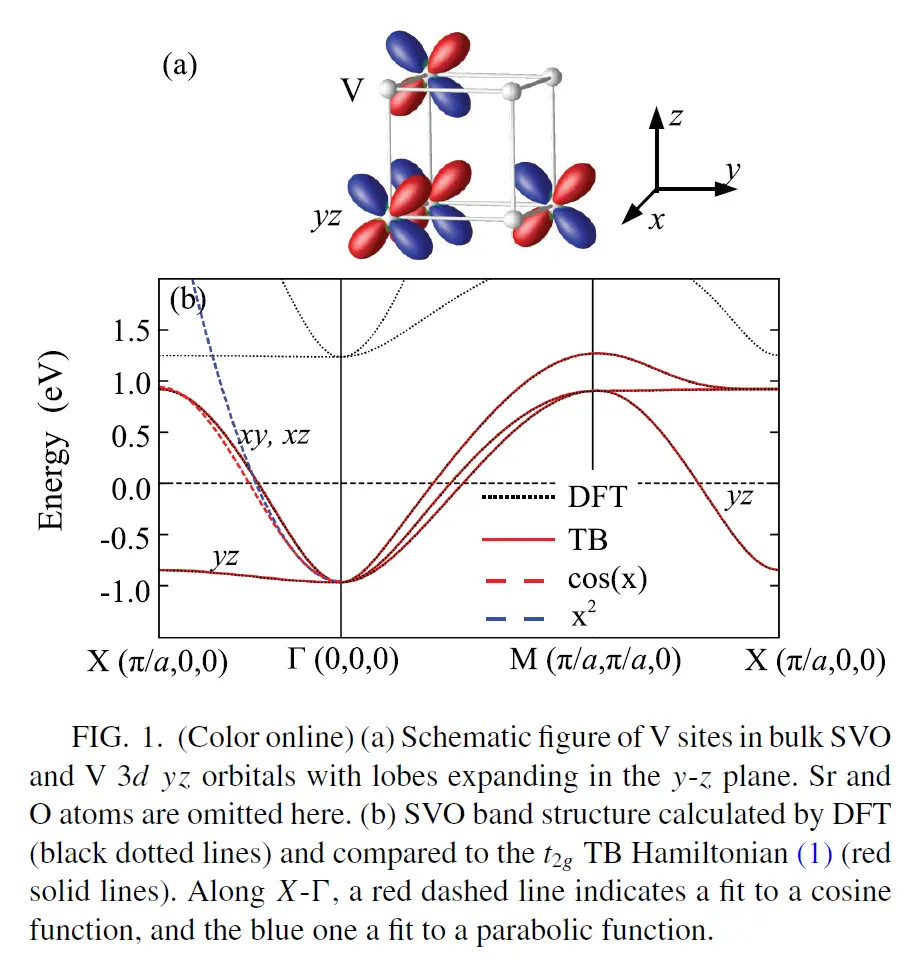
在PHYSICAL REVIEW B 88, 125401 (2013)中，利用以上方法对SVO块体的能带进行了紧束缚近似的拟合，发现和DFT计算所得的结果非常相近。而近自由电子近似方法得到的二次型的能带（蓝线）和DFT的计算结果差异较大，特别是在X点附近的色散，能量过高。

以上，本文提供了一种基于MATLAB的wannier90hr文件的提取脚本，能高效地选取出其中重要的信息。并结合一种高对对称的体系SVO，简单解释了如何根据hr文件中的信息，运用紧束缚近似方法画出体系的能带结构。

以上内容为本人自制，谢绝转载，欢迎转发。如有错误，欢迎指正。有问题欢迎在评论栏发起讨论。