MATLAB水温模型：零维模型计算与实现

B站内阅读体验可能不佳，可移步个人博客：http://blog.cjxyzhl.top/post/matlab/或者

CSDN：https://blog.csdn.net/weixin_45710019/article/details/105460195

零维水温模型

零维模型将整个湖泊水体看成是混合均匀的单元，如果湖（库）的水深和面积较小，水面风力所产生的掺混作用会使垂直方向的水温趋向一致，可以考虑采用零维模型来预测自然水温变化，也可以用来预测开式和闭式地表水源热泵系统运行时的水温变化。用零维模型计算出的水温是湖泊的整体平均水温。

基本方程

零维模型的基本方程如下：

注：这里特别说明方程左侧的时间单位为：s，而方程右侧所能拿到的数据为逐时，编程时需要单位换算

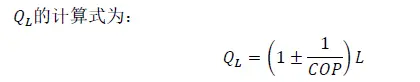
式中的L为空调负荷,COP为热泵机组的能效比。制冷运行时取加号，制热运行时取减号。如果令Q~L~=0，该方程便可用于计算湖泊的自然水温。

气象台站给出了相对湿度值，e_a为气温所对应的饱和水汽压与相对湿度的乘积。计算饱和水蒸气分压力的拟合公式较多，各公式的形式和计算精度都有所不同。 风速对水面换热有较大的影响。气象台给出的风速是距地面10m处的风速值，需要换算成1.5m处的风速，不同高度风速的换算公式为： :

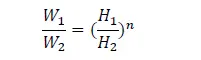
丘陵以及房屋比较稀疏的乡镇和城市郊区,n取0.16；有密集建筑群的城市市区，n取0.22；有密集建筑群且房屋较高的城市市区，n取0.3。

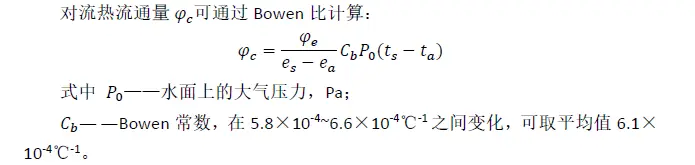
湖水与岩土的换热是指湖水与湖底及湖岸侧壁的换热，这项换热有利于减小水温的波动。要准确计算出这一换热量相当复杂，Hull等认为可将湖水与湖底的换热视为湖水与地下水之间的稳态传热过程，并采用以下的经验公式计算：

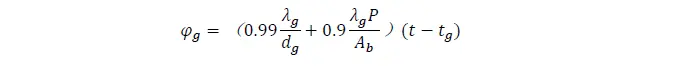
方程的右边为水温的非线性函数，且太阳辐射、气温等气象参数以及水体负 荷均为逐时变化的值，只能采用数值解法。采用“四阶龙格—库塔法求解"求解公式为：

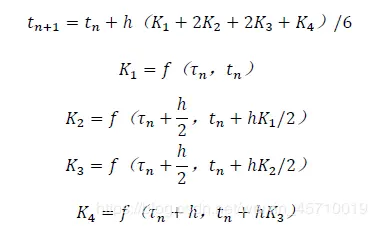
式中的h为时间步长。编写程序时需要将逐时的太阳辐射、气温、相对湿度、风速及空调负荷数据用txt文件的形式储存，程序运行时会自动调用这些数据。采用上式计算K~2~、K~3~时,各气象参数及空调负荷均采用前后两个时刻的算术平均值。

计算参数准备

水温模拟计算需要干球温度、相对湿度、辐射强度、风速、全年负荷等

相关数据可以到气象局网站查询，或者从DeST、鸿业EP等全年负荷模拟计算软件中导出相关气象参数。

matlab模型的建立

│  start.m        //启动函数 │   ├─main    //计算函数文件夹 │      ff.m │      fun.m │      psie.m │      psig.m │      psis.m │      QL.m │      runge.m │      testrk.m │      Tetens.m │       └─public  //计算数据文件夹        avgt.txt                         //逐时的平均气温        fengsu.txt                     //全年逐时风速        fuhe.txt                         //全年逐时负荷        fushe.txt      //全年逐时辐射        qiwen.txt      //全年逐时干球气温        shidu.txt      全年逐时相对湿度

四阶龙格—库塔法的matlab实现

runge函数为四阶龙格—库塔法的计算函数，需要输入x0,x1,y0,h等四项参数。 在该函数中，要引入相关全局变量，定义气象参数等随时刻数而变化的值；将相关逐时数据储存在txt或者excel文件中，在函数内使用load或xlsread命令读取数据，并将他们存储在相应的一维数组内，以便逐时计算时调用。

function [x, y] = runge(x0, x1, y0, h) addpath main public; global  ts ta psisr W1 es ea i L COP; position1=load('fushe.txt'); position2=load('qiwen.txt'); position3=load('fengsu.txt'); position4=load('shidu.txt'); position5=load('avgt.txt'); position6=load('fuhe.txt'); [A]=position2; [B]=position1; [C]=position3; [D]=position4; [E]=position5; [F]=position6; n = (x1 - x0) / h; x = zeros(n + 1,1); y = zeros(n + 1,1); x(1) = x0; y(1) = y0; for i = 1:n    ta=A(i)    ts=y(i);    psisr=B(i);    W1=C(i)*0.15^0.16;    es=Tetens(ts);    ea=Tetens(ta)*D(n)/100;    L=F(i)*1000;    COP=5;    x(i + 1) = x(i) + h;    k1 = fun(x(i), y(i));    %fun函数将微分方程中x,y的值赋给具体等式中的x,y，即该水温模型中的t    k2 = fun(x(i) + 0.5*h, y(i) + k1*h/2);    k3 = fun(x(i) + 0.5*h, y(i) + k2*h/2);    k4 = fun(x(i)+ h, y(i) + k3*h);    y(i + 1) = y(i) + h*(k1 + 2*k2 + 2*k3 + k4)/6; end end

水面的净流通量φ~s~的计算函数

函数内对于φ~e~的计算单独使用了函数φ~e~，因为这里涉及到与当时时刻气温的比较，不同结果对应了不同的计算式。

function psis = psis(ts,ta,psisr,W1,es,ea) addpath main public; %psis 水面的净热流通量，psisr-太阳辐射，psiar-大气长波辐射,rs-水面对太阳辐射的反射率,ra-水面对大气长波辐射的反射率，psiwe-水面发出的长波辐射,psic-蒸发 %psisr,es,ea,ta,W1, ra=0.03; rs=0.07; %psisr,es,ea,ta,W1, sigma=5.67e-8; Cr=0.17; omega=0.5; epsilonw=0.97; P0=97220; Cb=0.00061; %syms t; epsilona=(1-0.261*exp((-0.74e-4)*ta^2))*(1+Cr*omega^2); % Cr-由云层高确定的系数，omega-云层覆盖的比例 psiar=sigma*epsilona*(ta+273.15)^4; % sigma-Stefan-Boltzmann常数,epsilona-大气发射率,ta-气温 psiwr=sigma*epsilonw*(ts+273.15)^4; % epsilonw-水面长波发射率 psie1=psie(ts,ta,W1); % es-水面温度所对应的饱和水汽压，ea-空气的水汽压，W1-水面上方1.5米处的风速 psic=(psie1/(es-ea))*Cb*P0*(ts-ta); % P0-水面上的大气压力，Cb-Bowen常数 psis = (1-rs)*psisr+(1-ra)*psiar-psiwr-psie1-psic; end

下面是函数φ~e~

function psie = psie(ts,ta,W1) addpath main public; global es ea; if ts>ta    psie=0.01*(es-ea)*sqrt(22+12.5*W1^2+2*(ts-ta)); else    psie=0.01*(es-ea)*sqrt(22+12.5*W1^2); end

湖水与岩土的换热φ~g~的计算函数

这个函数中将包含式子中唯一的未知数t。

function psig = psig(t,Ab) addpath main public; %psig-湖水与岩土的换热量,lambdag-土壤的导热系数,P-湖面的周长,tg-当地的地下水温度 dg = 2; lambdag=2.78; P=954; tg=21; psig = (0.99*(lambdag/dg)+0.9*(lambdag*P/Ab))*(t-tg); % dg-地下水位与湖底之间的垂直距离，lambdag-土壤的导热系数，P-湖面的周长，tg-当地的地下水温度 end

方程右侧含t多项式的表示

testrk函数输出一个含t多项式，即为微分方程右侧的式子。

function f3 = testrk(A,Ab) addpath main public; global ts ta psisr W1 es ea i L; syms t; f1=psis(ts,ta,psisr,W1,es,ea); f2=psig(t,Ab); f4=QL(i,L); %如需计算引入负荷后的水温变化，则在下式中加入f4 f3=(A*f1-Ab*f2+f4)*3600/(1000*117600*4186); % 零维水温模型右侧等式 end

注：

f3=(Af1-Abf2+f4)3600/(1000117600*4186); 当中的3600，是用来统一时间单位的

对多项式中的t进行赋值

ff函数中使用matlabFunction函数，对含t未知数进行赋值

function k = ff(y) addpath main public; A=19600; Ab=29400; z=testrk(A,Ab); %实现水温模型右侧等式，即z=右侧等式 g=vpa(z,4) %化简代数式结果，保留4位小数 f=matlabFunction(z); %将z值赋给含t代数式中的t k = f(y); end

main文件夹中fun函数的说明

fun函数是多余的步骤，实现了将ff函数的结果传递作用，我这里以及完成水温模拟，便不进行修改了，大家模拟时可以将fun函数去除，直接使用ff函数。

function z = fun(x, y) addpath main public; z = ff(y); end

启动函数start.m

设置好相关参数后，在start函数内点击运行，模型便开始计算，结果将会储存在数组[x,y]中。

clear all; addpath main public; %将主函数及数据文件夹加入环境变量 x0 = 0; %初始时刻 x1 = 8759; %结束时刻 y0 = 7.5; %初始温度 h = 1; %计算步长 [x, y] = runge(x0, x1, y0, h); %将计算结果存在数组[x,y]中

B站投稿： https://space.bilibili.com/248367024 

代码仓库链接: https://github.com/952732328qwe/0-dimensional.