MATLAB生成STL文件：3D打印与模型导出

最近队友打算重复一篇文章，里边需要3D 打印一个元件用于调制太赫兹波，这个元件是一个高度不均的板子，各个点的高度 $g(x,y)$ 离散为一个矩阵 $g_{i,j}$ 表示，矩阵通过神经网络训练得到，于是我们就在想怎么把这个矩阵 g 保存成能3D打印的格式。

我一开始想的很简单，直接在网上找的一个matlab函数 surf2stl，然后把g作为输入，看结果才意识到这样输出来只是一个面，而不会是一个完整的物体，侧面和底面的数据又不确定应该以什么规则加进去，于是比较好奇stl 格式到底是怎么组成的，查到些资料，梳理下。

3D 打印最常见的格式是STL，stl 是stereolithography的缩写，它对三维模型的表面进行曲面细分（tessellation）分成小的三角形，在记录下每个三角形三个顶点的坐标以及三角形的指向方向（这里有冗余信息可以帮助判断文件是否损坏）。记录的方式有ascii 码和二进制两种，其中 ascii 记录格式如下：

solid &lt;name&gt;
  facet normal nx ny nz
    outer loop
        vertex v1x v1y v1z
        vertex v2x v2y v2z
        vertex v3x v3y v3z
    endloop
	endfacet
endsolid &lt;name&gt;

ascii 码方便人工调试，二进制则文件更小。

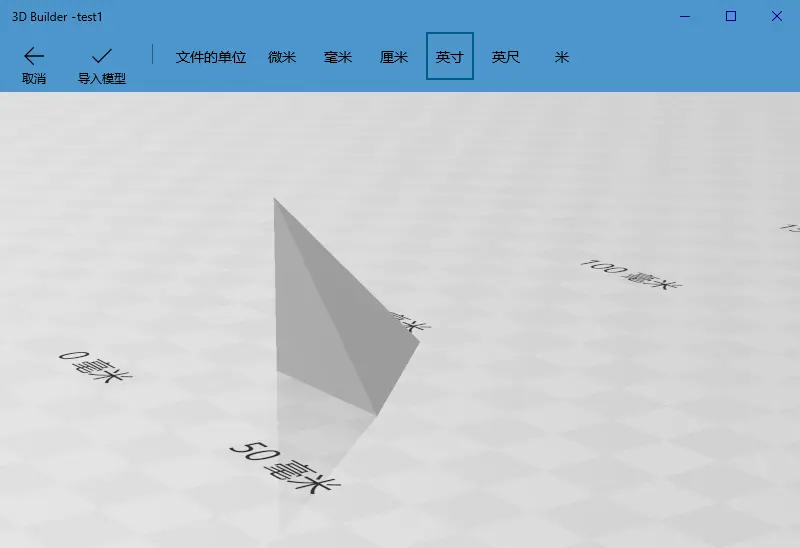
比如我们可以在记事本中输入这样一段：

solid
facet normal 0 0 1
outer loop
vertex 1 1 1
vertex 1 2 1
vertex 2 1 1
endloop
endfacet
facet normal 0 -1 0
outer loop
vertex 1 1 1
vertex 2 1 1
vertex 1 1 2
endloop
endfacet
facet normal -1 0 0
outer loop
vertex 1 1 1
vertex 1 2 1
vertex 1 1 2
endloop
endfacet
facet normal 0.5774 0.5774 0.5774
outer loop
vertex 2 1 1
vertex 1 2 1
vertex 1 1 2
endloop
endfacet
endsolid

文件后缀改成 stl 就能保存成一个四面体，用windows 自带的3D builder 打开（哈哈这个骚操作居然成功了）：

此外曲面细分还有一些规则，比如相邻三角形必须共用两个端点而不能是一个、所有坐标必须是正数。关于stl格式的介绍可以参考这个3D打印的网站：https://all3dp.com/1/stl-file-format-3d-printing/

知道了stl 格式的规则，我们就可以编写程序将数据排布成所需的顺序，再像上边的txt一样按格式写到文件里并存成stl；

其中一种比较简单的情况就是曲面是类似抛物面的“单向”曲面，而不是像圆一样，前者可以都能投影到一个由规则的小矩形网格组成的大矩形上，于是可以用X,Y,Z 三个矩阵记录下所有角点的位置，再把所有小矩形分割成两个三角形，最后写到stl 中。同时这一种曲面在matlab 中都能通过surf画出。matlab官网上给出了函数surf2stl实现这一功能，网址：

https://ww2.mathworks.cn/matlabcentral/fileexchange/4512-surf2stl

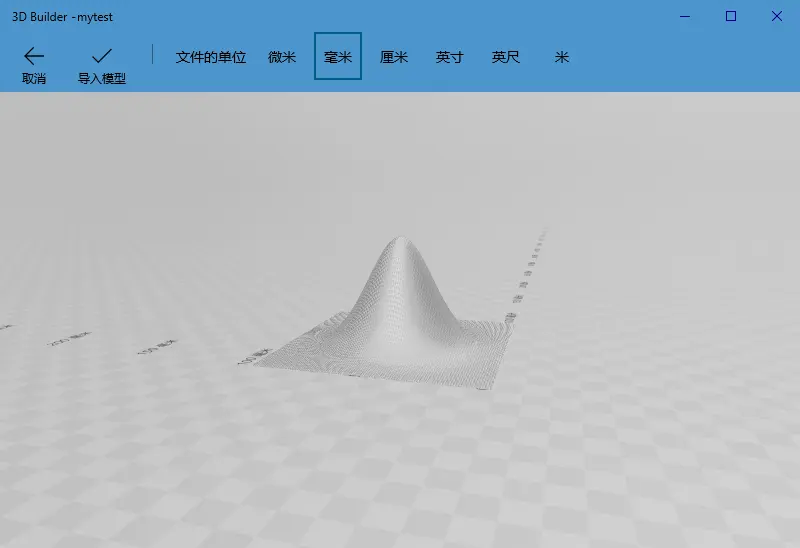
以下代码是在官网的 surf2stl 函数的基础上删改了一下，功能是以ascii方式输出一个高斯面：

x=1:100;
[X,Y]=meshgrid(x,x);
Z=50*exp(-1/(2*15^2)*((X-50).^2+(Y-50).^2));
Mysurf2stl(&#39;mytest.stl&#39;,X,Y,Z)

function f=Mysurf2stl(FileName,X,Y,Z)
fid=fopen(FileName,&#39;w&#39;);
fprintf(fid,&#39;solid\n&#39;);
for i=1:size(Z,1)-1
    for j=1:size(Z,2)-1

        %splitting each small rectangular to 2 small triangular
        p1=[X(i,j),Y(i,j),Z(i,j)];
        p2=[X(i+1,j),Y(i+1,j),Z(i+1,j)];
        p3=[X(i+1,j+1),Y(i+1,j+1),Z(i+1,j+1)];
    local_write_facet(fid,p1,p2,p3);

        p1=[X(i,j),Y(i,j),Z(i,j)];
        p2=[X(i,j+1),Y(i,j+1),Z(i,j+1)];
        p3=[X(i+1,j+1),Y(i+1,j+1),Z(i+1,j+1)];
    local_write_facet(fid,p1,p2,p3);
    end
end
fprintf(fid,&#39;endsolid&#39;);
fclose(fid);
f=1;
end

%to write a single small triangular to the file
function num = local_write_facet(fid,p1,p2,p3)
    num = 1;
    n = local_find_normal(p1,p2,p3);

        fprintf(fid,&#39;facet normal %.7E %.7E %.7E\r\n&#39;, n(1),n(2),n(3) );
        fprintf(fid,&#39;outer loop\r\n&#39;);
        fprintf(fid,&#39;vertex %.7E %.7E %.7E\r\n&#39;, p1);
        fprintf(fid,&#39;vertex %.7E %.7E %.7E\r\n&#39;, p2);
        fprintf(fid,&#39;vertex %.7E %.7E %.7E\r\n&#39;, p3);
        fprintf(fid,&#39;endloop\r\n&#39;);
        fprintf(fid,&#39;endfacet\r\n&#39;);

end

%to generate the normal direction vector n, from the vertex of triangular
function n = local_find_normal(p1,p2,p3)

v1 = p2-p1;
v2 = p3-p1;
v3 = cross(v1,v2);
n = v3 ./ sqrt(sum(v3.*v3));
end

输出：

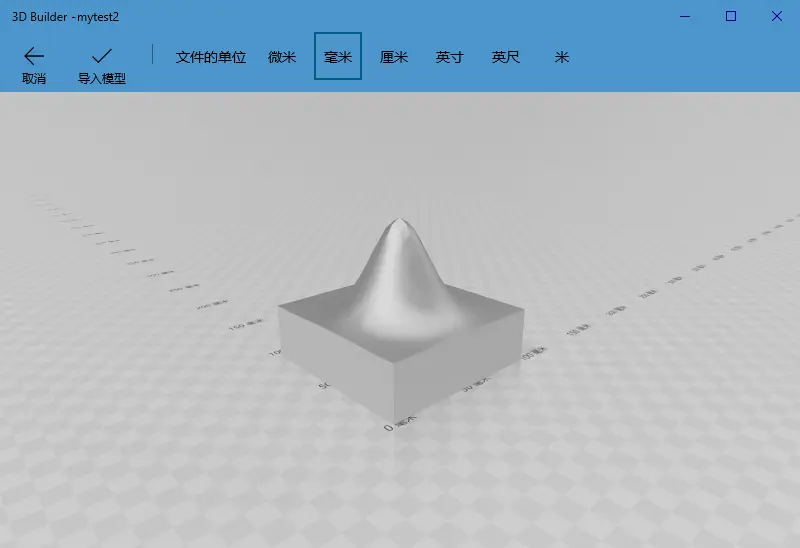
在这个基础上再添加侧面和底面，代码：

（之前的代码中有个小bug，Nx,Ny打错了导致只能生成底面为正方形的模型，感谢“白色的豌豆”指出，已修复）

%model2stl
x=2*(1:50);
y=1*(1:100);
[X,Y]=meshgrid(x,y);
Z=30+50*exp(-1/(2*15^2)*((X-50).^2+(Y-50).^2));
%Z=X+2;
model2stl(&#39;mytest2.stl&#39;,X,Y,Z)

function f=model2stl(FileName,X,Y,Z)
Nx=size(Z,2);
Ny=size(Z,1);
fid=fopen(FileName,&#39;w&#39;);
fprintf(fid,&#39;solid\n&#39;);
%top surface
Surf_write(fid,X,Y,Z,0)
%other surface assumed to be plane

%X=X(1,1) plane
Xs=zeros(2,Ny)+X(1,1);
Ys=[Y(:,1)&#39;;Y(:,1)&#39;];
Zs=[zeros(1,Ny);Z(:,1)&#39;];
Surf_write(fid,Xs,Ys,Zs,[-1,0,0])
%X=X(1,Nx) plane
Xs=zeros(2,Ny)+X(1,Nx);
Ys=[Y(:,Nx)&#39;;Y(:,Nx)&#39;];
Zs=[zeros(1,Ny);Z(:,Nx)&#39;];
Surf_write(fid,Xs,Ys,Zs,[1,0,0])
%Y=Y(1,1) plane
Ys=zeros(2,Nx)+Y(1,1);
Xs=[X(1,:);X(1,:)];
Zs=[zeros(1,Nx);Z(1,:)];
Surf_write(fid,Xs,Ys,Zs,[0,-1,0])
%Y=Y(Ny,1) plane
Ys=zeros(2,Nx)+Y(Ny,1);
Xs=[X(Ny,:);X(Ny,:)];
Zs=[zeros(1,Nx);Z(Ny,:)];
Surf_write(fid,Xs,Ys,Zs,[0,1,0])

%the bottom plane
Surf_write(fid,X,Y,0*Z,[0,0,-1])

fprintf(fid,&#39;endsolid&#39;);
fclose(fid);
end

function f=Surf_write(fid,X,Y,Z,opt)
for i=1:size(Z,1)-1
    for j=1:size(Z,2)-1

        %splitting each small rectangular to 2 small triangular
        p1=[X(i,j),Y(i,j),Z(i,j)];
        p2=[X(i+1,j),Y(i+1,j),Z(i+1,j)];
        p3=[X(i+1,j+1),Y(i+1,j+1),Z(i+1,j+1)];
    local_write_facet(fid,p1,p2,p3,opt);

        p1=[X(i,j),Y(i,j),Z(i,j)];
        p3=[X(i,j+1),Y(i,j+1),Z(i,j+1)];
        p2=[X(i+1,j+1),Y(i+1,j+1),Z(i+1,j+1)];
    local_write_facet(fid,p1,p2,p3,opt);
    end
end
f=1;
end

%to write a single small triangular to the file
function num = local_write_facet(fid,p1,p2,p3,opt)
    num = 1;
    n = local_find_normal(p1,p2,p3,opt);

        fprintf(fid,&#39;facet normal %.7E %.7E %.7E\r\n&#39;, n(1),n(2),n(3) );
        fprintf(fid,&#39;outer loop\r\n&#39;);
        fprintf(fid,&#39;vertex %.7E %.7E %.7E\r\n&#39;, p1);
        fprintf(fid,&#39;vertex %.7E %.7E %.7E\r\n&#39;, p2);
        fprintf(fid,&#39;vertex %.7E %.7E %.7E\r\n&#39;, p3);
        fprintf(fid,&#39;endloop\r\n&#39;);
        fprintf(fid,&#39;endfacet\r\n&#39;);

end

%to generate the normal direction vector n, from the vertex of triangular
function n = local_find_normal(p1,p2,p3,opt)
if ~opt
v2 = p2-p1;
v1 = p3-p1;
v3 = cross(v1,v2);
n = v3 ./ sqrt(sum(v3.*v3));
else
    n=opt;
end
end

结果：

返回上级列表

请

联系我们

，获取更多内容

< 上一篇: 回归预测：MATLAB实现CPO-LSSVM算法优化与应用

下一篇: MATLAB音乐演奏：第二期进阶教程 >