1. 欧拉法
由拉格郎日中值定理,在区间内必定存在
,使得:
所以。如果知道
,代入这个递推公式,那么递推过程得到的序列
,没有误差。但求
往往很困难,常用一个易求的值近似地代替
。显式欧拉法、隐式欧拉法、梯形公式法、中点欧拉方法的区别是对
和
的近似方法不同。
(1)显式欧拉法
显式欧拉法把近似为区间
的起点,即
显式欧拉法是单步法,每一轮递推只用到前面一轮递推的结果。欧拉公式具有明显的几何意义,就是用折线近似代替方程的解曲线,因而常称为欧拉折线法。由泰勒展开式可知显式欧拉法具有1阶精度。
显式欧拉法在步长过大时误差较大;在步长较小时需要多步递推,可能出现误差累积的现象。由于显式欧拉法的精度不高,因此在实际应用中用的较少。
(2)隐式欧拉法
隐式欧拉法把近似为区间
的终点,即
隐式欧拉法是隐式方法,递推公式的右端包含未知量,故隐式欧拉法需要求解方程,得出
。
为避免求解方程,常用显式欧拉法的计算结果作为迭代的初值,把隐式欧拉法的递推公式作为迭代公式反复迭代,得到迭代序列
。如果步长
足够小,那么迭代序列收敛于
。
隐式欧拉法具有1阶精度。
(3)梯形公式法
梯形公式法把近似为区间
的起点和终点导数的平均值。递推公式为:
显然,梯形公式法是隐式方法,需要求解方程。为避免解方程,常用显式欧拉法的计算结果作为迭代的初值,把梯形公式法的递推公式作为迭代公式反复迭代,得到迭代序列
。如果步长
足够小,那么迭代序列收敛于
。
梯形公式法具有2阶精度。
(4)中点欧拉法
中点欧拉法把近似为区间
的中点
,即
中点欧拉方法是双步法,需要2个初值和
才能启动递推过程。一般先用单步法由点
计算出
,再用中点欧拉方法反复地递推。
中点欧拉方法具有2阶精度。
(5)改进的欧拉法
改进的欧拉法是一种预测—校正方法,它的每一轮递推包括预测和校正这2个步骤:
(1)先用显式欧拉公式计算出,
,即预测;
(2)再用梯形公式迭代一次,即校正。
改进的欧拉法精度比显式欧拉法高,不需要解方程,是一种更实用的方法。
2. 欧拉法MATLAB算法实现
如下算法实现五种形式的欧拉法,根据用户选择ode_method的方法,采用不同的欧拉法求解。
function sol = ODEEulerMethod(ode_fun, x0, y0, varargin)
%% 欧拉法求解一阶微分方程,包括显式、隐式、梯形、中点和预测校正法
% 1. ode_fun:待求解的微分方程
% 2. x0,y0为初值值
% 3. x_final为求解区间的终点
% 4. h为求解步长
% 5. ode_method,求解欧拉方法
% 输出参数sol为解的结构体
%% 1.输入参数的判别与处理
args = inputParser; % 函数的输入解析器
addParameter(args, 'x_final', 1); % 设置变量名xfinal和默认参数
addParameter(args, 'h', 0.05); % 设置变量名h和默认参数
addParameter(args, 'ode_method', "pc"); % 设置变量名h和默认参数
parse(args,varargin{:}); % 对输入变量进行解析,如果检测到前面的变量被赋值,则更新变量取值
h = args.Results.h; % 步长
x_final = args.Results.x_final; % 求解区间的终点
ode_method = args.Results.ode_method; % 求解方法
%% 2. 必要参数初始化
x_i = x0:h:x_final; % 待求解ode区间的离散数值
ode_sol = zeros(length(x_i), 2); % ode的数值解
ode_sol(:, 1) = x_i; % 第一列的值存储待求x
%% 3. 根据不同的欧拉方法选择不同的求解函数
if lower(ode_method) == "explicit"
ode_sol(:, 2) = explicit_euler(ode_fun, x_i, y0, h);
sol.ode_method = "Explicit Euler";
elseif lower(ode_method) == "implicit"
y_e = explicit_euler(ode_fun, x_i, y0, h); % 显示欧拉法的解
ode_sol(:, 2) = implicit_euler(ode_fun, x_i, y0, h, y_e);
sol.ode_method = "Implicit Euler";
elseif lower(ode_method) == "trapezoid"
y_e = explicit_euler(ode_fun, x_i, y0, h); % 显示欧拉法的解
ode_sol(:, 2) = trapezoid_euler(ode_fun, x_i, y0, h, y_e);
sol.ode_method = "Trapezoid Euler";
elseif lower(ode_method) == "middle"
ode_sol(:, 2) = middle_euler(ode_fun, x_i, y0, h);
sol.ode_method = "Middle Euler";
elseif lower(ode_method) == "pc"
ode_sol(:, 2) = pc_euler(ode_fun, x_i, y0, h);
sol.ode_method = "PC Euler";
else
disp("仅支持 explicit 、implicit 、trapezoid 、middle 和 和 PC.")
exit(0)
end
%% 4. 对应不同欧拉法的不同函数
function y = explicit_euler(odefun, xi, y0, h)
% 显式欧拉法
y = zeros(length(xi), 1); % 用于存储微分方程数值解
y(1) = y0; % 第一个值为初始值
% 从第二个值开始求解
for i = 1:length(xi) - 1
y(i + 1) = y(i) + h * odefun(xi(i), y(i)); % 显式欧拉公式
end
end
function y = implicit_euler(odefun, xi, y0, h, ye)
% 隐式欧拉法
y = zeros(length(xi), 1); % 用于存储微分方程数值解
y(1) = y0; % 第一个值为初始值
for i = 1:length(xi) - 1
% 用显式欧拉法的计算结果ye作为迭代的初值
x_n = y(i) + h * odefun(xi(i + 1), ye(i + 1));
x_b = inf;
% 把隐式欧拉法的递推公式作为迭代公式反复迭代
while abs(x_n - x_b) > 1e-12
x_b = x_n; % 迭代值的更新
% 不断用隐式欧拉公式逼近精度
x_n = y(i) + h * odefun(xi(i + 1), x_b);
end
y(i + 1) = x_n; % 满足精度的隐式解
end
end
function y = trapezoid_euler(odefun, xi, y0, h, ye)
% 梯形欧拉法(隐式方法)
y = zeros(length(xi), 1);
y(1) = y0;
for i = 1:length(xi) - 1
f_val = odefun(xi(i), y(i)); % 当前方程右端函数值
% 用显式欧拉法的解作为其初始解
x_n = y(i) + h / 2 * (f_val + odefun(xi(i + 1), ye(i + 1)));
x_b = inf;
% 把梯形欧拉法的递推公式作为迭代公式反复迭代
while abs(x_n - x_b) > 1e-12
x_b = x_n; % 迭代值的更新
% 不断用梯形欧拉公式逼近精度
x_n = y(i) + h / 2 * (f_val + odefun(xi(i + 1), x_b));
end
y(i + 1) = x_n; % 满足精度的隐式解
end
end
function y = middle_euler(odefun, xi, y0, h)
% 中点欧拉法,递推前需要两个起始值
y1 = y0 + h * odefun(xi(1), y0); % 起始的第2个值
y = zeros(length(xi), 1); % 用于存储微分方程数值解
y(1) = y0; % 第1个值为初始值
y(2) = y1; % 递推起始的第2个值
% 从第3个值开始求解
for i = 2:length(xi) - 1
y(i + 1) = y(i - 1) + 2 * h * odefun(xi(i), y(i)); % 中点欧拉公式
end
end
function y = pc_euler(odefun, xi, y0, h)
% 改进(预测+校正)的欧拉法
y = zeros(length(xi), 1); % 用于存储微分方程数值解
y(1) = y0; % 第1个值为初始值
% 从第2个值开始求解
for i = 1:length(xi) - 1
y_predict = y(i) + h * odefun(xi(i), y(i)); % 显式欧拉法预测
% 梯形欧拉法校正
y(i + 1) = y(i) + h / 2 * (odefun(xi(i), y(i)) + odefun(xi(i + 1), y_predict));
end
end
%% 5. 输出参数结构体的构造
sol.ode_sol = ode_sol; % 数值解
sol.h = h; % 求解步长
sol.span = [x0, x_final]; % 求解区间
end
3. 欧拉法算法测试
例1:采用五种欧拉法求解一阶微分方程,已知解析解为。
测试代码如下:
clc, clear, close all
x0 = 0; % 初值
y0 = 1; % 初值
h = 0.05; % 求解步长
x_final = 1; % 求解区间的终点
sol_e = ODEEulerMethod(@ode_fun, x0, y0, "x_final", x_final, "h", h, "ode_method", "explicit"); % 显式
sol_i = ODEEulerMethod(@ode_fun, x0, y0, "x_final", x_final, "h", h, "ode_method", "implicit"); % 隐式
sol_t = ODEEulerMethod(@ode_fun, x0, y0, "x_final", x_final, "h", h, "ode_method", "Trapezoid"); % 梯形
sol_m = ODEEulerMethod(@ode_fun, x0, y0, "x_final", x_final, "h", h, "ode_method", "middle"); % 中点
sol_pc = ODEEulerMethod(@ode_fun, x0, y0, "x_final", x_final, "h", h, "ode_method", "pc"); % 预测校正法
xi = 0:h:1; % 求解区间的数值离散化
yi = sqrt(1 + 2 * xi); % 对应的精确解
subplot(121)
plot(xi, yi, "k-", "LineWidth", 1) % 精确解曲线
hold on
sol = [sol_e.ode_sol, sol_i.ode_sol, sol_t.ode_sol, sol_m.ode_sol, sol_pc.ode_sol]; % 组合数值解
for i = 1:5
plot(sol(:, i * 2 - 1), sol(:, i * 2), "-", "LineWidth", 1) % 可视化各欧拉法的数值解
end
grid on; grid minor; box off
legend("Exact Sol", "Explicit", "Implicit", "Trapezoid", "Middle", "PC", "Location", "best")
legend("boxoff")
title("欧拉法数值解曲线 h = " + string(h))
xlabel("$x$", "interpreter", "latex")
ylabel("$y(x)$", "interpreter", "latex")
subplot(122)
err_l2 = zeros(5, 1); % 存储误差范数
err_l2(1) = sum((sol_e.ode_sol(:, 2) - yi').^2); % 计算数值解与精确解误差的平方和
plot(sol_e.ode_sol(:, 1), sol_e.ode_sol(:, 2) - yi', "-", "LineWidth", 1)
hold on
for i = 2:5
err_l2(i) = sum((sol(:, i * 2) - yi').^2);
plot(sol(:, i * 2 - 1), sol(:, i * 2) - yi', "-", "LineWidth", 1)
end
grid on; grid minor; box off
legend("Explicit err = " + string(err_l2(1)), "Implicit err = " + string(err_l2(2)), ...
"Trapezoid err = " + string(err_l2(3)), "Middle err = " + string(err_l2(4)), ...
"PC err = " + string(err_l2(5)), "Location", "best")
legend("boxoff")
xlabel("$x$", "interpreter", "latex")
ylabel("$\sum(y - \hat y)^{2}$", "interpreter", "latex")
title("误差曲线 h = " + string(h))测试结果:输出参数为结构体,如显式欧拉法的输出结果:
>> sol_e
sol_e =
包含以下字段的 struct:
ode_method: "Explicit Euler"
ode_sol: [21×2 double]
h: 0.0500
span: [0 1]可视化图像如图1和图2所示,可见较小的步长可获得较高的精度,但注意计算时的舍入误差和误差累积。
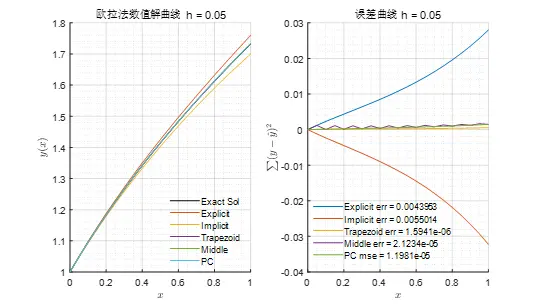
图1 步长为0.05时的欧拉法数值解曲线与误差曲线
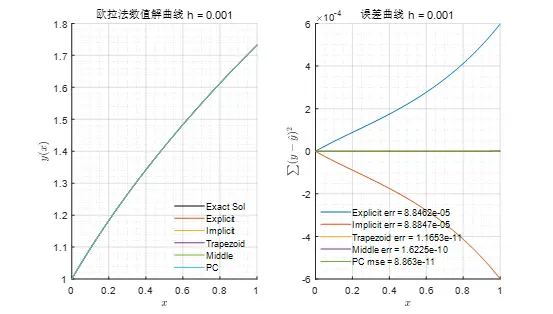
图2 步长为0.001时的欧拉法数值解曲线与误差曲线