4 湍流
4.1 湍流模拟的一般原则
4.1.1 雷诺(系综)平均
雷诺平均中,瞬时(精确)NS方程的求解变量被分解为平均值(系综平均或时间平均)和波动分量。对速度分量:
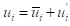
类似的,对压力和其他标量:
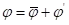
可以表示压力、能量或种类浓度。
将上述表达式代入瞬时连续性方程和动量方程,并取时间(或系综)平均,去掉平均速度上的横线,得到系综平均动量方程:
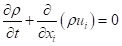
时均的连续性方程(质量守恒)
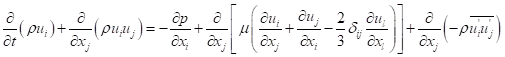
上面两个式子合起来叫做RANS方程。他们与瞬时NS方程具有相同的形式,速度和其他解变量表示系综(时间)平均值。多出来的最后一项表示湍流的影响, 雷诺应力必须被建模以封闭时均动量方程。
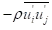
对于变密度流动,上面两个式子叫做Favre-averaged NS方程,速度代表质量平均值。因此,这两个式子适用于变密度流。
4.1.2 滤波NS方程
通过在傅里叶(波数)空间或构型(物理)空间中过滤与时间相关的Navier-Stokes方程,可以获得大涡模拟所采用的控制方程。过滤过程有效地过滤掉了尺度小于计算中使用的过滤宽度或网格间距的涡流。因此,由此产生的方程控制着大漩涡的动力学。
(过程略)
4.1.3 混合RANS-LES简述
起初,雷诺平均和空间滤波的概念似乎不兼容,因为它们会导致动量方程中出现不同的附加项(Reynolds Stresses雷诺应力和sub-grid stresses亚网格应力)。这将排除混合模型,如尺度自适应模拟(SAS)、分离涡模拟(DES)、屏蔽分离涡模拟(SDES)或应力混合涡模拟(SBES),这些模型基于整个区域RANS和LES部分的一组动量方程。然而,重要的是要注意,一旦湍流模型被引入动量方程,它们就不再携带任何有关其来源(平均)的信息。举个例子,RANS和LES中最流行的模型都是涡粘性模型,用于替代雷诺应力张量或亚网格应力张量。在引入涡粘性(湍流粘性)后,RANS和LES动量方程在形式上是相同的。差异完全在于底层湍流模型提供的涡流粘度的大小。这使得可以在不对动量方程进行任何形式更改的情况下,通过适当降低LES区域的涡流粘度制定湍流模型,从RANS模式切换到LES模式。
4.1.4 Boussinesq方法vs雷诺应力传输模型
湍流建模的雷诺平均方法要求对雷诺应力进行适当建模。一种常用的方法是利用Boussinesq假设将雷诺应力与平均速度梯度联系起来:
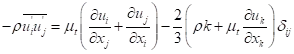
雷诺应力的计算
Boussinesq假设用于SA模型、ke系列模型和kw系列模型。这种方法的优点是与湍流粘度计算相关的计算成本相对较低。在SA模型的情况下,只需求解一个额外的输运方程(表示湍流粘度μt)。在和模型的情况下,求解了两个附加的输运方程(用于湍流动能k,以及湍流耗散率e或比耗散率w),μt作为k和e或k和w的函数进行计算。所提出的Boussinesq假设的缺点是,它假设的是一个各向同性的标量,这严格来说是不正确的。然而,各向同性湍流粘度的假设通常适用于仅由一个湍流剪切应力控制的剪切流。这涵盖了许多技术流程,如壁面边界层、混合层、射流等。
RSM中包含的另一种方法是求解雷诺应力张量中每个项的输运方程。还需要一个额外的比例确定方程(通常用于k或w)。这意味着在二维流动中需要五个额外的输运方程,而在三维流动中必须求解七个额外的输运方程。
在许多情况下,基于Boussinesq假设的模型表现良好,雷诺应力模型的额外计算费用是不合理的。然而,在湍流各向异性对平均流量有主导影响的情况下,RSM显然更优越。这种情况包括高旋流和应力驱动的二次流。
4.2 SA模型
4.2.1 概述
Spalart-Allmaras模型是一个单方程模型,用于求解运动涡(湍流)粘度的模拟输运方程。SA模型是专门为涉及壁面有界流动的航空航天应用而设计的,并已被证明对承受逆压梯度的边界层具有良好的结果。它在涡轮机械应用中也越来越受欢迎。
SA模型的原始形式实际上是一种低雷诺数模型,需要正确解析边界层的粘性影响区域(y+~1网格)。在ANSYS Fluent中,SA模型已通过y+不敏感的壁面处理进行了扩展,这使得模型的应用与近壁y+分辨率无关。该方法自动从粘性子层公式混合到基于y+的对数公式。在中间网格上(y+=1~30),公式保持其完整性,并提供一致的壁面剪应力和传热系数。尽管y+敏感度被去除,仍应确保边界层的最小分辨率为10-15个单元。
SA模型是针对空气动力流动开发的。它没有针对一般的工业流动进行校准,对于一些自由剪切流,尤其是平面和圆形射流,它会产生相对较大的误差。此外,它不能用来预测均匀各向同性湍流的衰减。
4.2.2 SA模型的输运方程
SA模型中的输运变量(niu波浪)与湍流运动粘度μt相同,但近壁(粘度影响)区域除外。修正湍流粘度(niu波浪)的输运方程为:
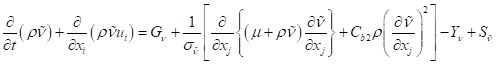
SA模型主体
G是湍流粘度的产生,Y是在近壁区由于壁面阻塞和粘性阻尼而引起的湍流粘性的破坏,S是用户自定义的源项。(niu)是分子运动粘度。(西格玛niu波浪)和(Cb2)是常数。注意,由于SA模型中未计算湍流动能,因此在估算雷诺应力时,表达式中的最后一项(含湍动能项)被忽略。
4.2.3 湍流粘度建模
湍流粘度μt由下式计算:
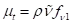
SA模型对湍流黏度建模
粘性阻尼函数fv1由下式计算:
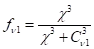
粘性阻尼函数
且:
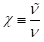
系数
4.2.4 湍流生成建模
生成项,G被建模为:
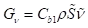
湍流生成项建模
而:
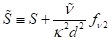
S波浪
且:
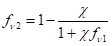
系数
其中,Cb1和k为常数,d为到壁面的距离,S是变形张量的标量度量。默认在ANSYS Fluent中,与原始SA摸样一样,基于涡量的大小定义,即:
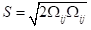
变形张量的标量度量
其中Ωij是平均旋转速率张量,即:
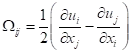
平均旋转速率张量
默认表达式的理由是,对于剪切流,vorticity涡度和应变率是相同的。vorticity涡度的优点是在停滞线等无粘性流动区域为零,在这些区域,由于应变率产生的湍流可能是非物理的。然而,ANSYS Fluent集成并提供了一个替代公式。
这种修正将涡度和应变张量的测量结合起来,定义为:
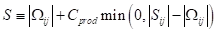
修正的变形张量的标量度量
其中,
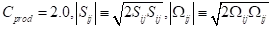
系数
且平均应变率定义为
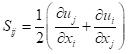
平均应变率
包括旋转张量和应变张量会减少涡流粘度的产生,从而在涡度测量值超过应变率测量值的区域降低涡流粘度本身。一个这样的例子可以在涡旋流中找到,也就是说,受纯旋转影响的涡旋核心附近的流动,其中湍流被抑制。包括旋转张量和应变张量更准确地解释了旋转对湍流的影响。默认选项(仅包括旋转张量)倾向于过度预测涡流粘度的产生,导致过度预测涡流内部的涡流粘度本身。
4.2.5 湍流破坏建模
破坏项被建模为:
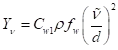
湍流破坏项建模
其中:
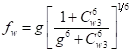
系数
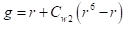
系数

系数
Cw1,Cw2和Cw3为常数。注意,上述(包括平均应变对S的影响的)修改,也将影响(S波浪)用于计算r的值。
4.2.6 模型常数
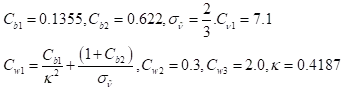
SA模型中的常数
4.2.7 壁面边界条件
SA模型在ANSYS Fluent中进行了扩展,采用了一种y+不敏感的壁面处理方法,可以自动混合粘性子层公式中的所有解变量
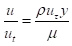
到相应的取决于y+的对数层值。
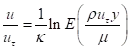
其中,u是与壁面平行的速度,(u涛)是摩擦速度,y是到壁面的间距,k是冯卡门常数(0.4187),E=9.783。
对混合进行校准,以覆盖缓冲层(y+1~30)中的中间y+值
4.2.7.1 用于结冰模拟的SA模型的处理
(内容略)
4.2.8 对流传热和质量输送建模
在ANSYS Fluent中,湍流热传输采用雷诺类比湍流动量传递的概念进行建模。“建模”能量方程如下所示:
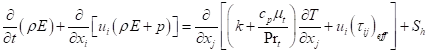
能量方程
k在这里是热传导系数,E是总能,偏应力张量定义为:
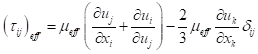
偏应力张量
4.3 标准、RNG、和Realizable k-e模型
4.4 标准、BSL、和SSTkw 模型
4.5 Generalized (GEKO) 模型
4.6 k-kl-w模型
4.7 转捩SST模型
4.8 间歇转捩模型
4.9 V2F模型
4.10 雷诺应力模型RSM
4.11 尺度自适应模型SAS
4.12 分离涡模型DES
4.13 屏蔽分离涡模型SDES
4.14 应力混合涡模型SBES
4.15 大涡模拟模型LES
4.16 嵌入式大涡模拟模型ELES
4.17 壁面湍流的近壁处理
4.18 SA和两方程模型的曲率矫正
4.19 两方程模型的产生限制器
4.20 湍流阻尼
4.21 湍流尺度的定义