Robotics Toolbox机械臂机器人仿真应用

RoboticsToolbox基础用法

1）二维空间位姿描述

二维空间位姿变换示例

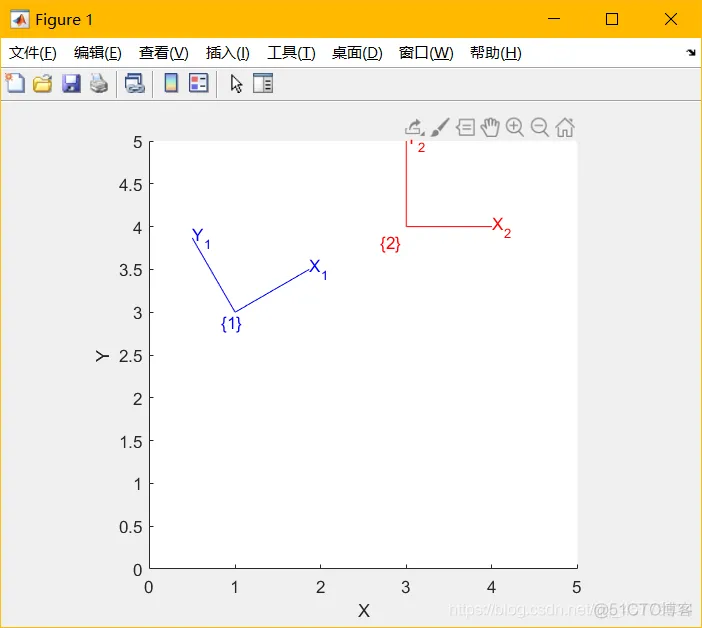
T1 = SE2(1,3,30,"deg");trplot2(T1,"frame","1","color","b");axis([0 5 0 5]);T2=trans12(3, 4);
hold on;trplot2(T2,"frame","2","color","r");1.2.3.4.5.6.

运行效果：

2）三维空间位姿描述

正交旋转矩阵

三维空间位姿变换示例

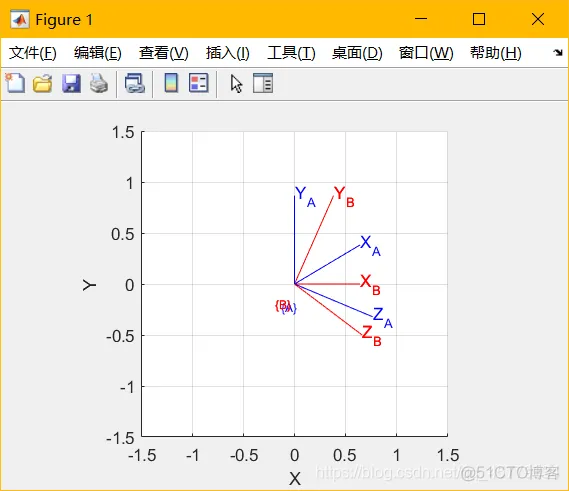
R1=rotx(30,"deg")*roty(50,"deg"); %绕x轴旋转30°，再绕y轴旋转50°trplot(R1,"frame","A", "color", "b"); 
%画出旋转矩阵R1tranimate(R1,"frame","A", "color", "b"); %将R1的变换做成动画R2=roty(50,"deg")*rotx(30,"deg"); 
%绕y轴旋转50°，再绕x轴旋转30°hold ontrplot(R2,"frame","B", "color", "r"); 
%画出旋转矩阵R2tranimate(R2,"frame","B", "color", "r"); %将R2的变换做成动画1.2.3.4.5.6.7.

运行效果：

R1和R2是两个完全不同的旋转矩阵，说明R1和R2具有不可交性。

2.三角度表示法

（1）欧拉角

欧拉角是在

示例：欧拉角与旋转矩阵的相互转化

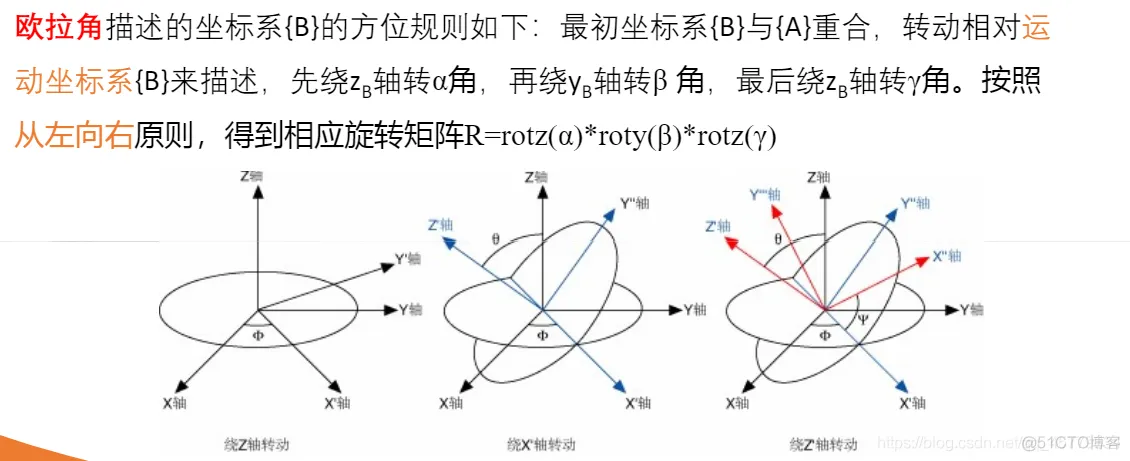
R3=rotz(0.1)*roty(0.2)*rotz(0.3); % 构造旋转矩阵R3R4=eul2r(0.1,0.2,0.3);
 % 欧拉角转化为旋转矩阵eul=tr2eul(R3); % 旋转矩阵转化为欧拉角1.2.3.

2）RPY角

RPY角是在固定坐标系A下，以固定的XYZ轴作为旋转的基准。三个角分别为Row（回转），Pitch（俯仰）和Yaw（偏转），可以用右手坐标系表示，食指为Row，中指为Pitch，大拇指为Yaw。

示例：RPY角与旋转矩阵的相互转化

R5=rotz(0.3)*roty(0.2)*rotx(0.1); % 构造旋转矩阵R5R6=rpy2r(0.3,0.2,0.1); 
% rpy角转化为旋转矩阵eul=tr2rpy(R5); % 旋转矩阵转化为rpy角1.2.3.

3）双向量角表示法

示例：双向量转化为旋转矩阵

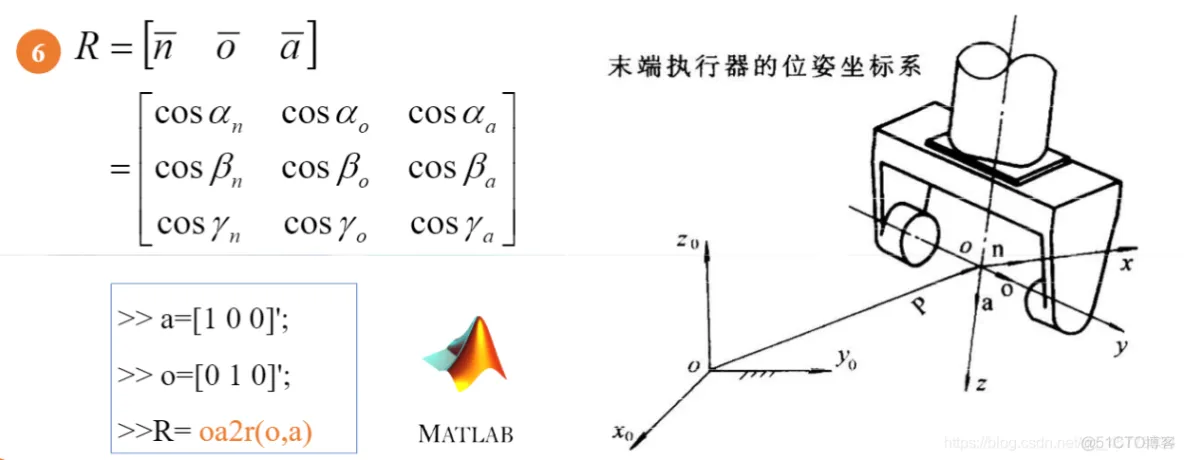
a=[1 0 0]';o=[0 1 0]';R7=oa2r(o,a); % 将双向量o,a转化为旋转矩阵R71.2.3.

4）向量和旋转角表示法

示例：向量旋转角与旋转矩阵的相互转化

5）单位四元数表示法

示例：四元数用法

s=0.98335;v=[0.034271, 0.10602, 0.14357];Q=UnitQuaternion(s,v); % 组成四元数q=Q.inv(); % 求共轭Q.display(); % 打印出四元数Q.plot(); % 画出出四元数Q.animate(); % 动画展示四元数TT=Q.T; % 制作齐次变换矩阵RR=Q.R; % 制作旋转矩阵rpy=Q.torpy(); % 转换成rpy角eul=Q.toeul(); % 转换成eul角1.2.3.4.5.6.7.8.9.10.11.

3.RoboticsToolbox建立机器人模型

（1）建立机器人模型函数

Link类函数

Seriallink类函数

（2）DH参数

标准DH参数

改进DH参数

（3）改进DH参数，建立机器人模型步骤

示例

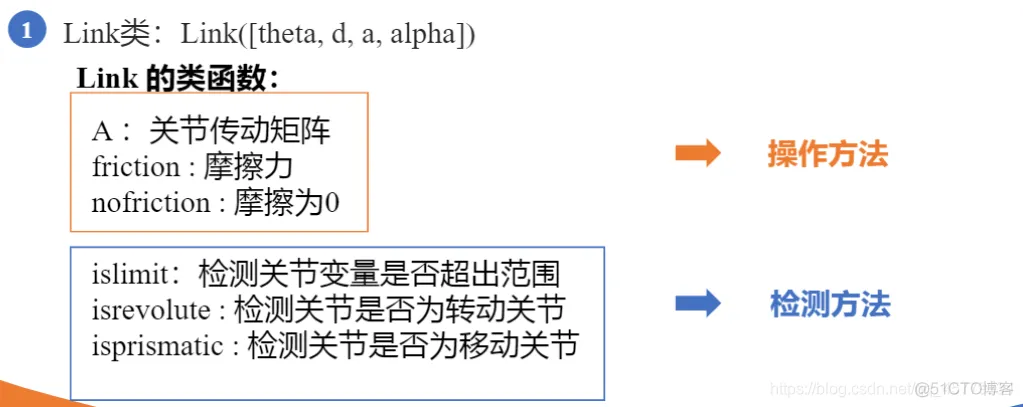
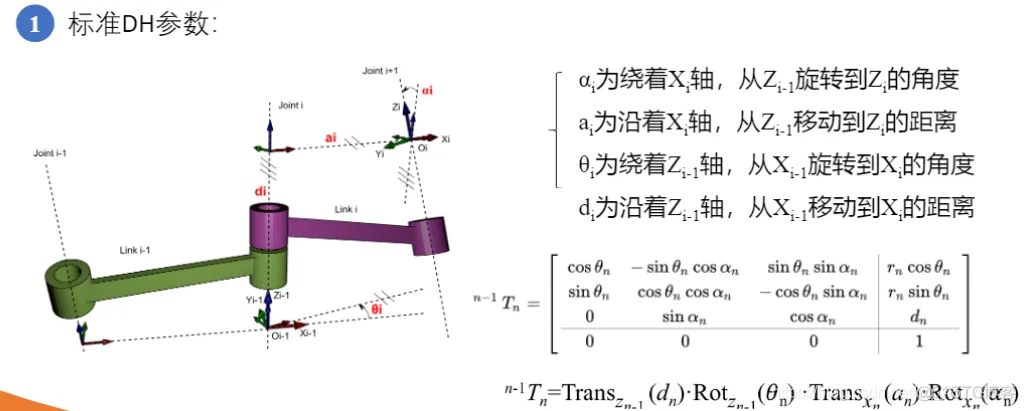
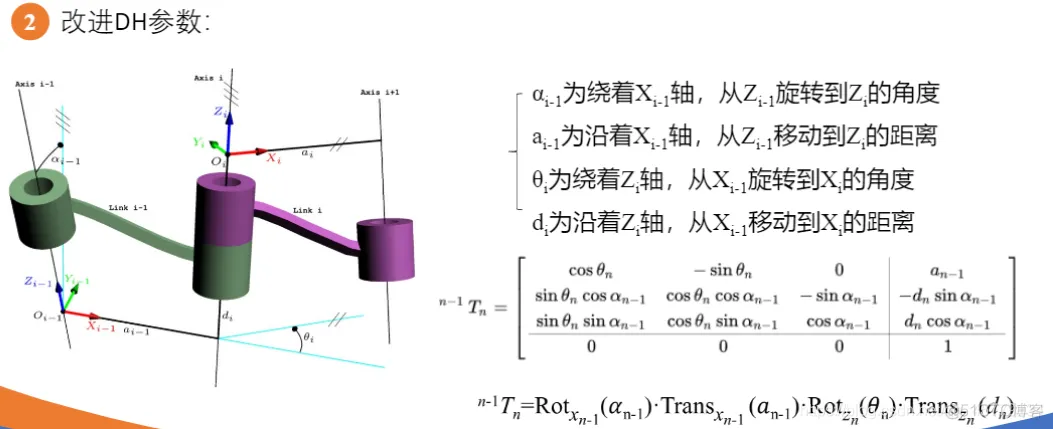
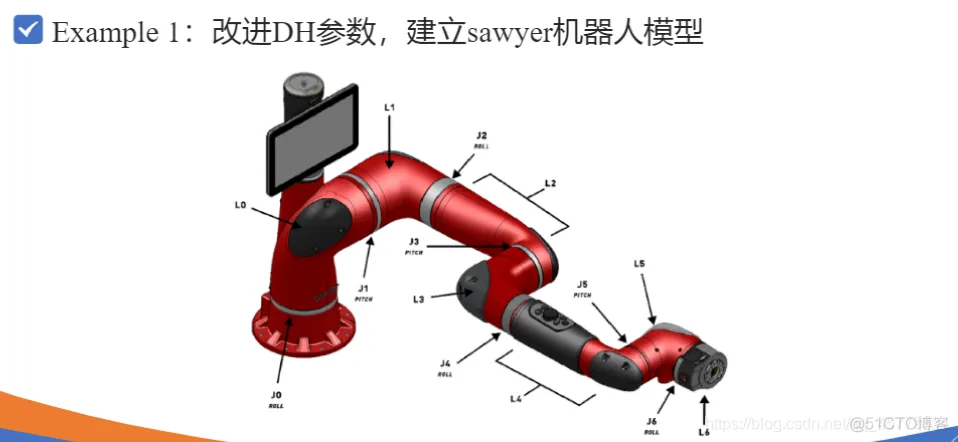
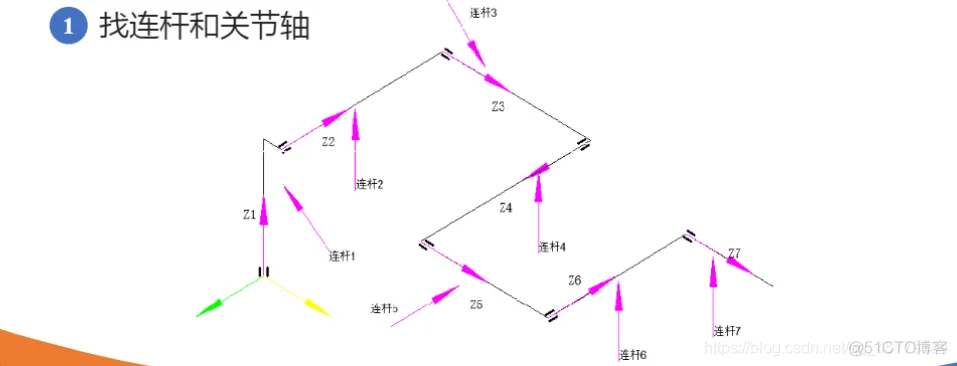
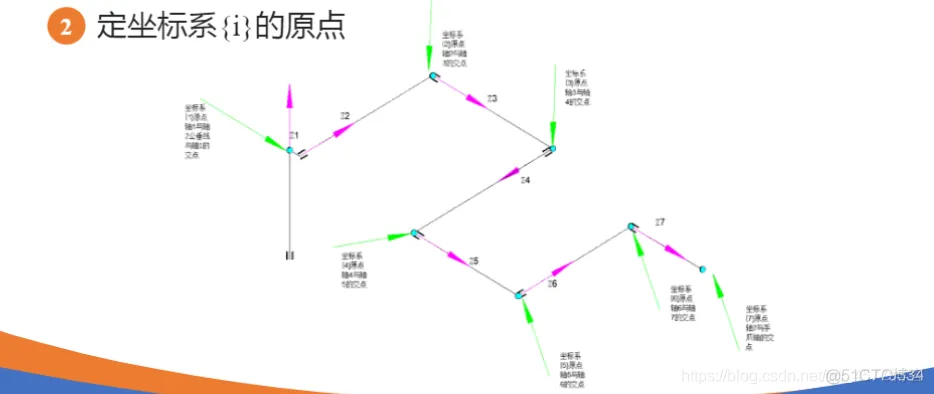
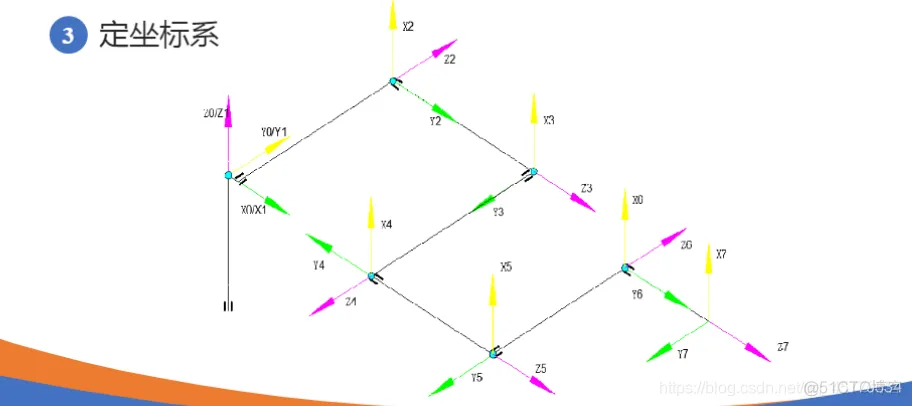
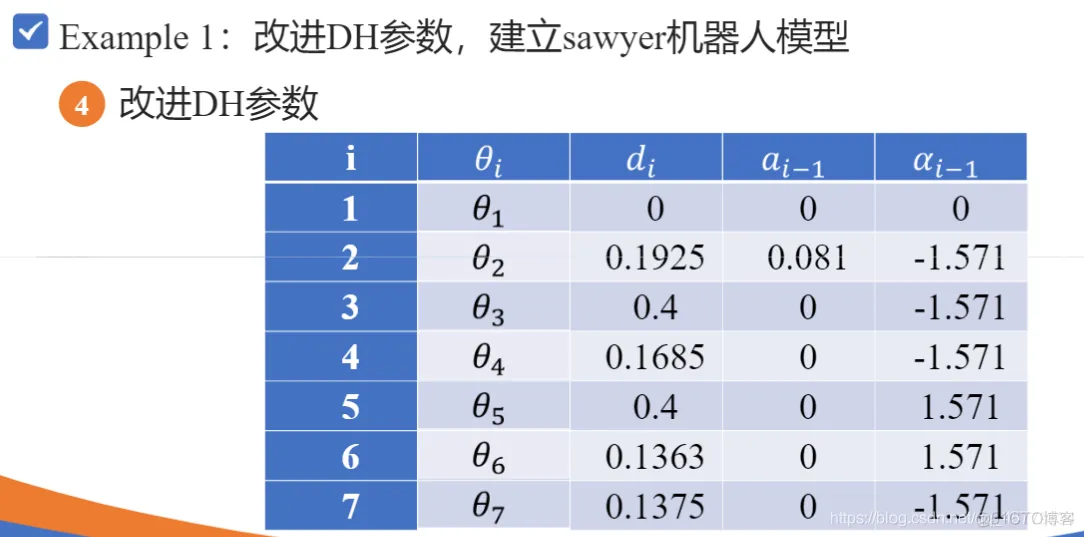
clc;clear;% 定义各个连杆以及关节类型，默认为转动关节%           theta      d        a        alpha%               连杆偏距参数d 连杆长度参数 关节偏角参数alphaL1=Link([     0        0        0          0], 'modified'); % [四个DH参数], optionsL2=Link([    -pi/2   0.1925,   0.081     -pi/2], 'modified');L3=Link([     0       0.4       0        -pi/2], 'modified');L4=Link([     0      0.1685,    0        -pi/2], 'modified');L5=Link([     0      0.4,       0         pi/2], 'modified');L6=Link([     0      0.1363     0         pi/2], 'modified');L7=Link([     0      0.13375    0        -pi/2], 'modified');% b=isrevolute(L1);robot=SerialLink([L1,L2,L3,L4,L5,L6,L7]); % 将七个连杆组成机械臂robot.name='modified sawyer';robot.display(); % 展示出view(3); % 解决robot.teach()和plot的索引超出报错robot.teach();robot.plot([0 -pi/2 0 0 0 0 0]);1.2.3.4.5.6.7.8.9.10.11.12.13.14.15.16.17.18.19.20.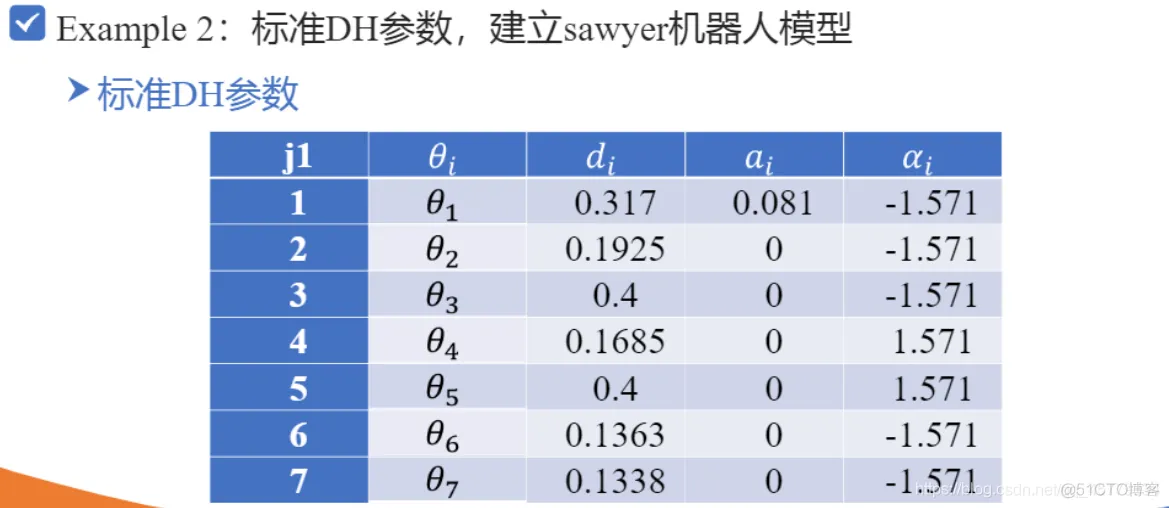

（4）标准DH参数建模

clc;clear;% 定义各个连杆以及关节类型，默认为转动关节%           theta      d        a        alpha%               连杆偏距参数d 连杆长度参数 关节偏角参数alphaL1=Link([     0        0        0          0], 'standard'); % [四个DH参数], optionsL2=Link([    -pi/2   0.1925,   0.081     -pi/2], 'standard');L3=Link([     0       0.4       0        -pi/2], 'standard');L4=Link([     0      0.1685,    0        -pi/2], 'standard');L5=Link([     0      0.4,       0         pi/2], 'standard');L6=Link([     0      0.1363     0         pi/2], 'standard');L7=Link([     0      0.13375    0        -pi/2], 'standard');% b=isrevolute(L1);robot=SerialLink([L1,L2,L3,L4,L5,L6,L7]); % 将七个连杆组成机械臂robot.name='standard sawyer';robot.display(); % 展示出view(3); % 解决robot.teach()和plot的索引超出报错robot.teach();robot.plot([0 -pi/2 0 0 0 0 0]);1.2.3.4.5.6.7.8.9.10.11.12.13.14.15.16.17.18.19.20.

（5）标准DH和改进DH的区别

4.正逆运动学、轨迹规划

（1）正运动学

puma560机械臂正运动学示例

mdl_puma560; % 加载puma560模型qz    % 零角度qr    % 就绪状态，机械臂甚至且垂直qs    % 伸展状态，机械臂伸直且水平qn    % 标准状态，机械臂处于灵巧工作状态view(3);p560.plot(qn);T=p560.fkine(qn);1.2.3.4.5.6.7.8.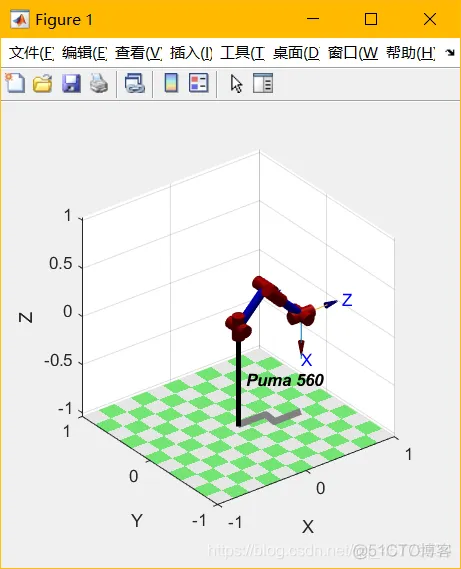

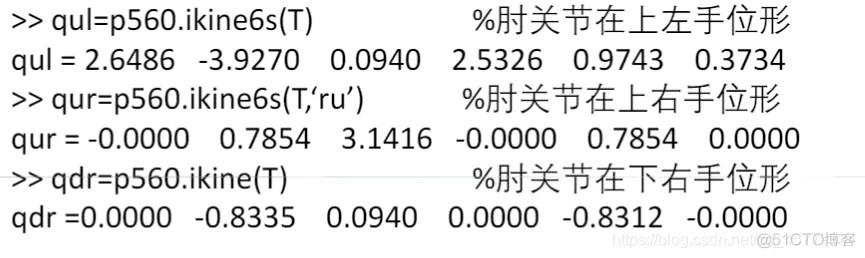
2）逆运动学

puma560机械臂逆运动学示例

（3）轨迹规划

示例：sawyer机器人轨迹规划

clc;clear;% 定义各个连杆以及关节类型，默认为转动关节%           theta      d        a        alpha%               连杆偏距参数d 连杆长度参数 关节偏角参数alphaL1=Link([     0        0        0          0], 'modified'); % [四个DH参数], optionsL2=Link([    -pi/2   0.1925,   0.081     -pi/2], 'modified');L3=Link([     0       0.4       0        -pi/2], 'modified');L4=Link([     0      0.1685,    0        -pi/2], 'modified');L5=Link([     0      0.4,       0         pi/2], 'modified');L6=Link([     0      0.1363     0         pi/2], 'modified');L7=Link([     0      0.13375    0        -pi/2], 'modified');% b=isrevolute(L1);robot=SerialLink([L1,L2,L3,L4,L5,L6,L7],'name','FANUC'); % 将七个连杆组成机械臂robot.name='modified sawyer';robot.display(); % 展示出init_ang=[0 0 0 0 0 0 0];targ_ang=[pi/4,-pi/3,pi/5,pi/2,-pi/4,pi/2,pi/3];step=200;[q,qd,qdd]=jtraj(init_ang,targ_ang,step); %关节空间规划轨迹，得到机器人末端运动的[位置，速度，加速度]T0=robot.fkine(init_ang); % 正运动学解算Tf=robot.fkine(targ_ang);subplot(2,4,3); i=1:7; plot(q(:,i)); title("位置"); grid on;subplot(2,4,4); i=1:7; plot(qd(:,i)); title("速度"); grid on;subplot(2,4,7); i=1:7; plot(qdd(:,i)); title("加速度"); grid on;Tc=ctraj(T0,Tf,step);Tjtraj=transl(Tc);subplot(2,4,8); plot2(Tjtraj, 'r');title('p1到p2直线轨迹'); grid on;subplot(2,4,[1,2,5,6]);plot3(Tjtraj(:,1),Tjtraj(:,2),Tjtraj(:,3),"b"); grid on;hold on;view(3); % 解决robot.teach()和plot的索引超出报错qq=robot.ikine(Tc);robot.plot(qq);1.2.3.4.5.6.7.8.9.10.11.12.13.14.15.16.17.18.19.20.21.22.23.24.25.26.27.28.29.30.31.32.33.34.35.36.37.38.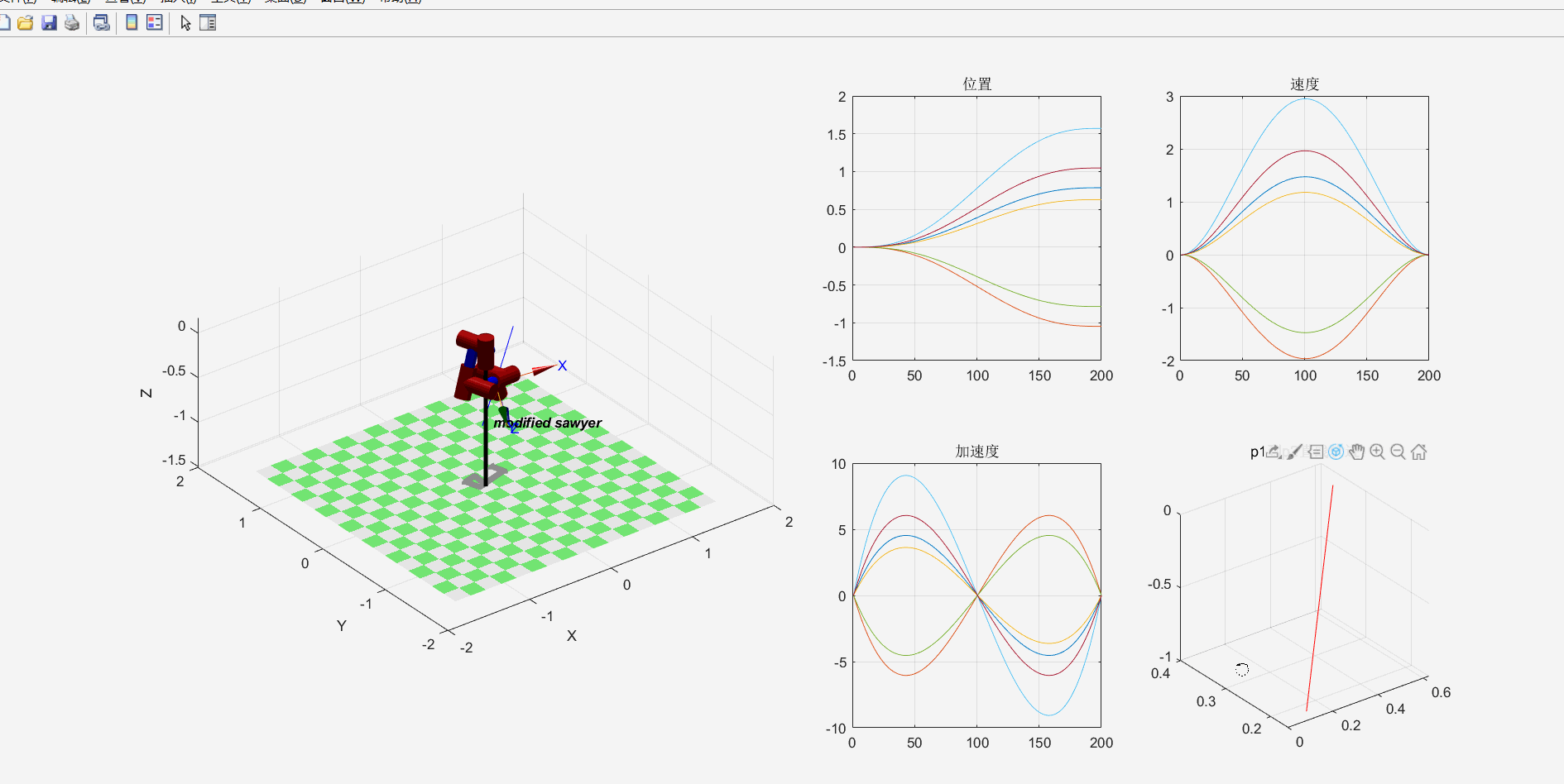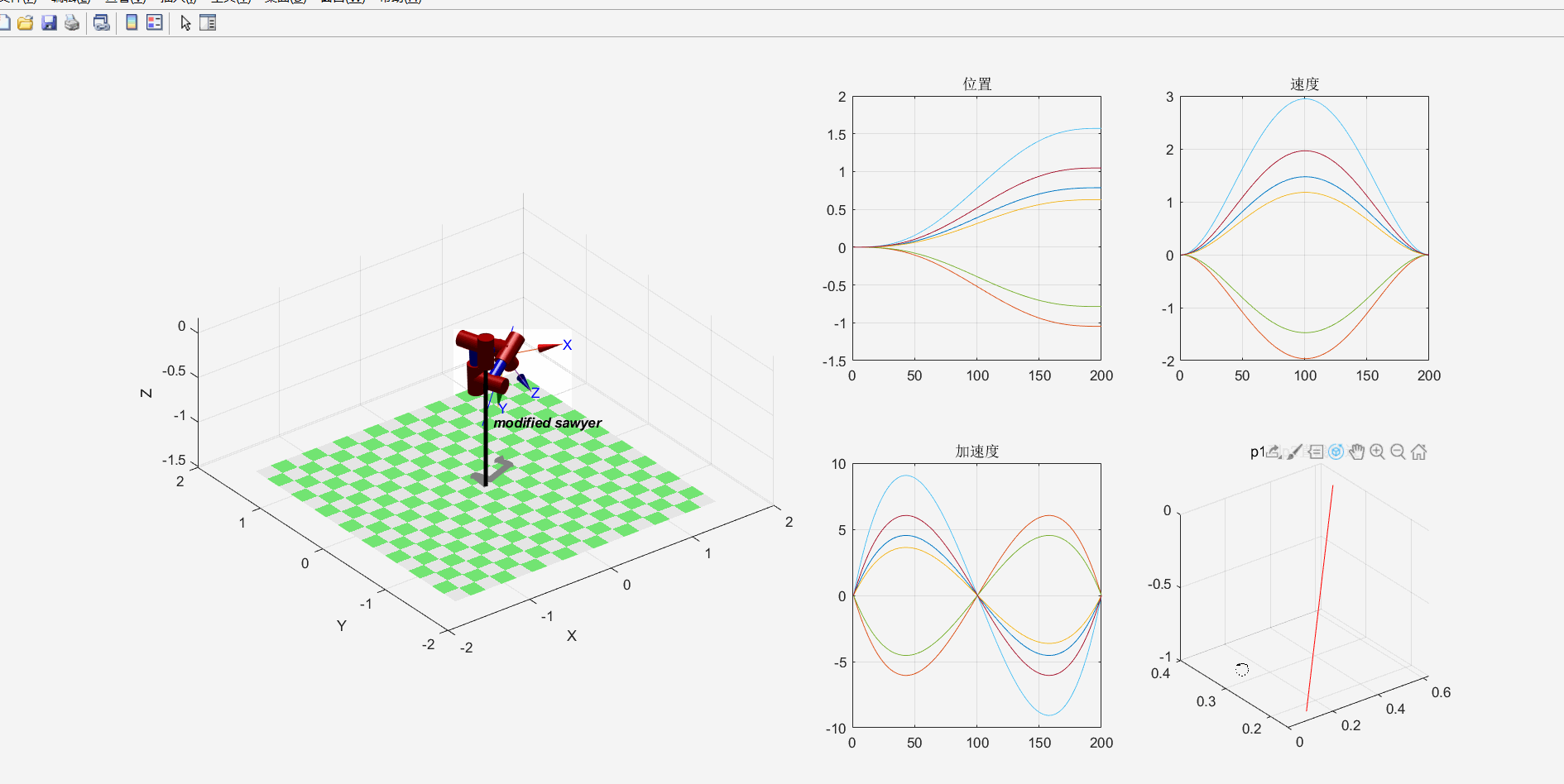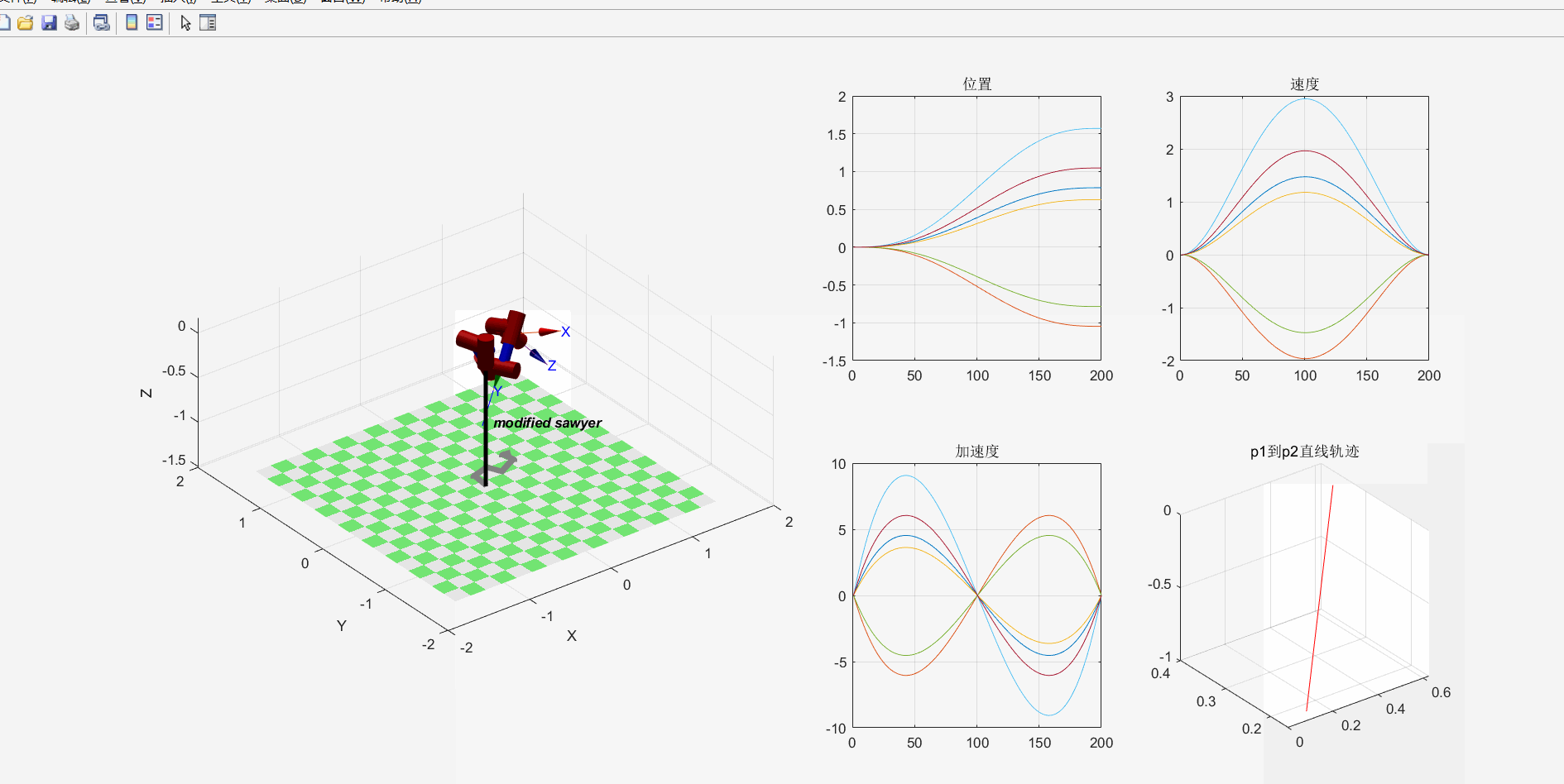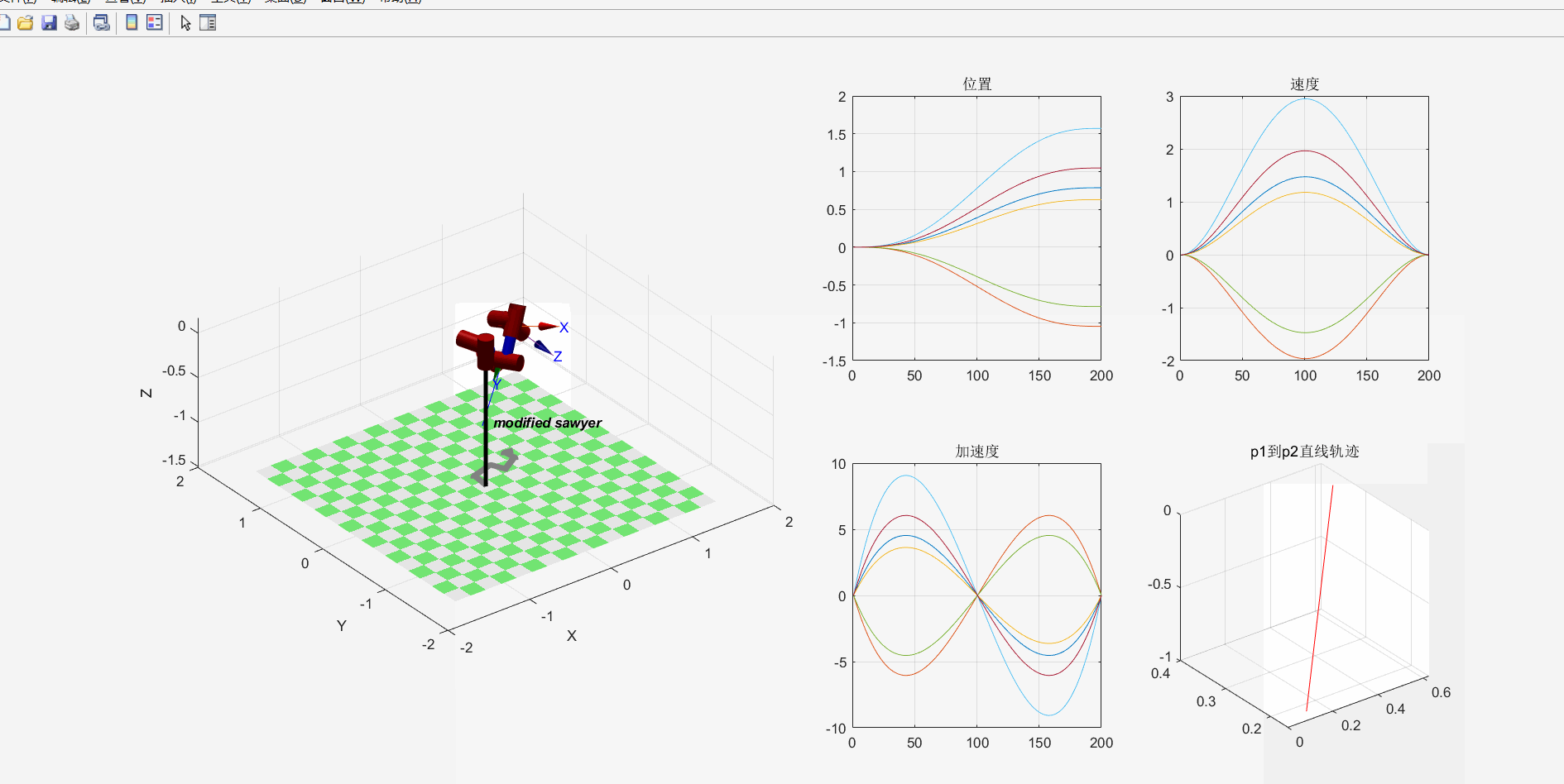

5.速度和静力

（1）雅可比矩阵

（2）分解速度运动控制

免责声明：本文系网络转载或改编，未找到原创作者，版权归原作者所有。如涉及版权，请联系删