本文主要参考MATLAB帮助文件,Illustrating Three approaches to GPU Computing: The Mandelbrot Set,也可在网页https://ww2.mathworks.cn/help/parallel-computing/illustrating-three-approaches-to-gpu-computing-the-mandelbrot-set.html上看到同样的内容,代码如下:
clc
close all
maxIterations = 500;
gridSize = 2000;
xlim = [-1.5, 0.6];
ylim = [ -1.2, 1.2];
%% ------CPU计算------
%%%% Setup
t = tic();
x = linspace(xlim(1), xlim(2), gridSize);
y = linspace(ylim(1), ylim(2), gridSize);
[xGrid,yGrid] = meshgrid(x, y);
z0 = xGrid + 1i*yGrid;
count = ones(size(z0));
%%%% Calculate
z = z0;
for n = 0:maxIterations
z = z.*z + z0;
inside = abs(z)<=2;
count = count + inside;
end
count = log(count); %取对数运算不是必须,但能提高图像对比度
%%%% Show
cpuTime = toc(t);
% fig = gcf;
% fig.Position = [200 200 600 600];
imagesc(x, y, count);
% colormap([jet();flipud(jet());0 0 0]);
axis off
title(sprintf('%1.2fsecs (without GPU)', cpuTime));
%% ------native GPU------
%%%% Setup
t = tic();
x = gpuArray.linspace(xlim(1), xlim(2), gridSize);
y = gpuArray.linspace(ylim(1), ylim(2), gridSize);
[xGrid,yGrid] = meshgrid(x, y);
z0 = complex(xGrid, yGrid);
count = ones(size(z0), 'gpuArray');
%%%% Calculate
z = z0;
for n = 0:maxIterations
z = z.*z + z0;
inside = (abs(z)<=2);
count = count + inside;
end
count = log(count); %取对数运算不是必须,但能提高图像对比度
%%%% Show
count = gather(count); % Fetch the data back from the GPU
naiveGPUTime = toc(t);
figure
imagesc(x, y, count)
axis off
title(sprintf('%1.3fsecs (native GPU) = %1.1fx faster', ...
naiveGPUTime, cpuTime/naiveGPUTime))
%% ------GPU arrayfun------
%%%% Setup
t = tic();
x = gpuArray.linspace(xlim(1), xlim(2), gridSize);
y = gpuArray.linspace(ylim(1), ylim(2), gridSize);
[xGrid,yGrid] = meshgrid(x, y);
%%%% Calculate
count = arrayfun(@pctdemo_processMandelbrotElement, ...
xGrid, yGrid, maxIterations);
% 此处的arrayfun会调用pctdemo_processMandelbrotElement.m,
% 该m文件的内容附在后面。如果在这一行报错,请把
% pctdemo_processMandelbrotElement.m复制到当前m文件的目录下。
%%%% Show
count = gather(count); % Fetch the data back from the GPU
gpuArrayfunTime = toc(t);
figure
imagesc(x, y, count)
axis off
title(sprintf('%1.3fsecs (GPU arrayfun) = %1.1fx faster', ...
gpuArrayfunTime, cpuTime/gpuArrayfunTime));
%% ------GPU CUDA------
%%%% Load the kernel
cudaFilename = 'pctdemo_processMandelbrotElement.cu';
ptxFilename = ['pctdemo_processMandelbrotElement.',parallel.gpu.ptxext];
kernel = parallel.gpu.CUDAKernel(ptxFilename, cudaFilename);
%%%% Setup
t = tic();
x = gpuArray.linspace(xlim(1), xlim(2), gridSize);
y = gpuArray.linspace(ylim(1), ylim(2), gridSize);
[xGrid,yGrid] = meshgrid(x, y);
%%%% Make sure we have sufficient blocks to cover all of the locations
numElements = numel(xGrid);
kernel.ThreadBlockSize = [kernel.MaxThreadsPerBlock,1,1];
kernel.GridSize = [ceil(numElements/kernel.MaxThreadsPerBlock),1];
%%%% Call the kernel
count = zeros(size(xGrid), 'gpuArray');
count = feval(kernel, count, xGrid, yGrid, maxIterations, numElements);
%%%% Show
count = gather(count); % Fetch the data back from the GPU
gpuCUDAKernelTime = toc(t);
figure
imagesc(x, y, count)
axis off
title(sprintf('%1.3fsecs (GPU CUDAKernel) = %1.1fx faster', ...
gpuCUDAKernelTime, cpuTime/gpuCUDAKernelTime));本机配置:CPU AMD Ryzen5 3600,GPU:RTX 3060,在maxIterations = 500;gridSize = 2000;xlim = [-1.5, 0.6];ylim = [ -1.2, 1.2];的条件下,生成的图片如下,计算耗时分别是9.89s,2.448s(4倍),0.232s(42.7倍),0.068s(144.6倍),

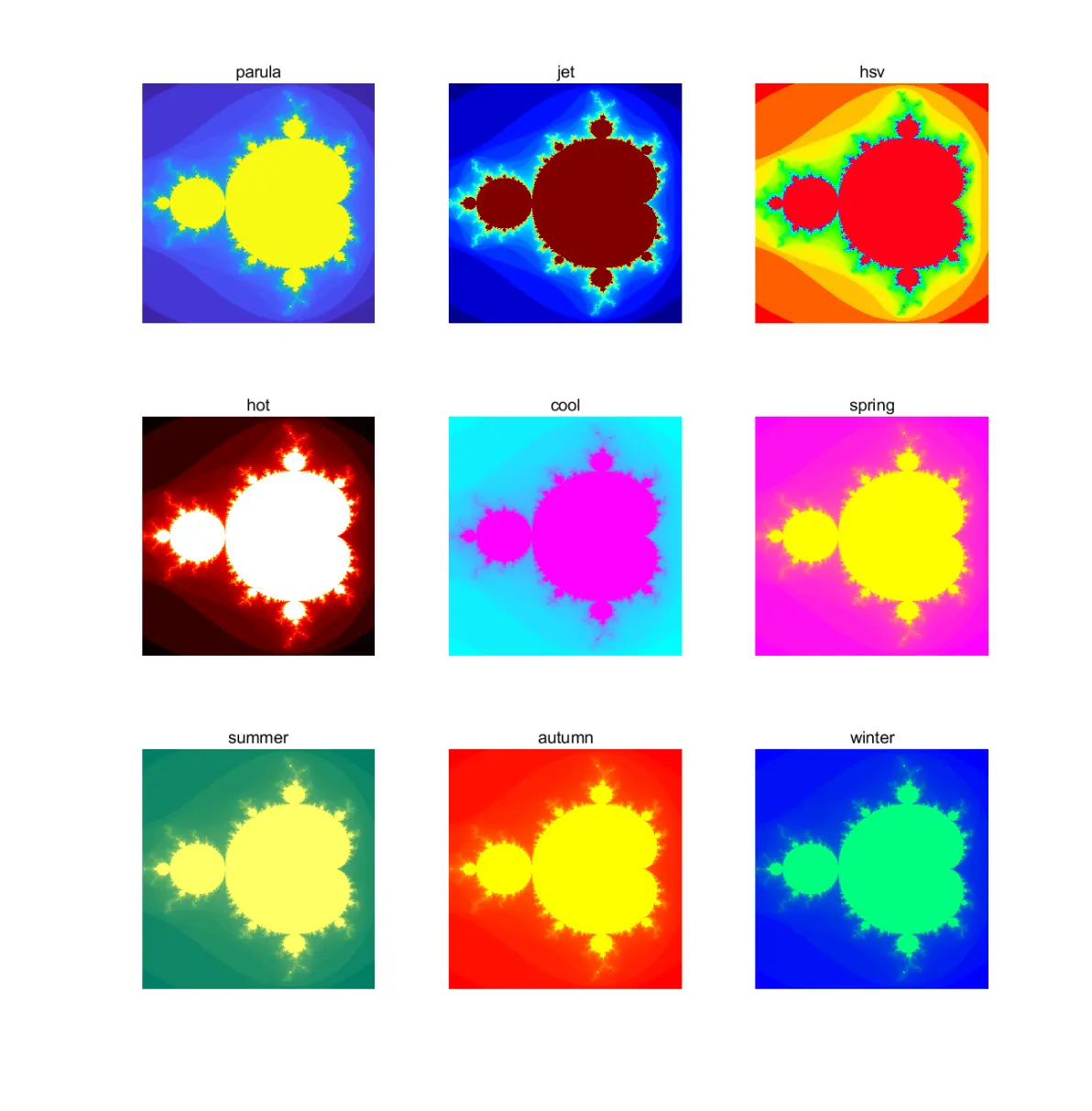
可以用colormap函数改颜色,可选参数有parula,jet,hsv,hot,cool,spring,summer, autumn,winter,gray,bone,copper,pink,lines,colorcube,prism,flag,white

count = log(count); 取对数运算不是必须,但能提高图像对比度,不取对数的效果如下,可以看出周围小分支的清晰度下降

pctdemo_processMandelbrotElement.cu、.m、.ptx···在MATLAB安装路径下,内容分别如下:
/**
* @file pctdemo_processMandelbrotElement.cu
* CUDA code to calculate the Mandelbrot Set on a GPU.
* Copyright 2011 The MathWorks, Inc.
*/
/** Work out which piece of the global array this thread should operate on */
__device__ size_t calculateGlobalIndex() {
// Which block are we?
size_t const globalBlockIndex = blockIdx.x + blockIdx.y * gridDim.x;
// Which thread are we within the block?
size_t const localThreadIdx = threadIdx.x + blockDim.x * threadIdx.y;
// How big is each block?
size_t const threadsPerBlock = blockDim.x*blockDim.y;
// Which thread are we overall?
return localThreadIdx + globalBlockIndex*threadsPerBlock;
}
/** The actual Mandelbrot algorithm for a single location */
__device__ unsigned int doIterations( double const realPart0,
double const imagPart0,
unsigned int const maxIters ) {
// Initialise: z = z0
double realPart = realPart0;
double imagPart = imagPart0;
unsigned int count = 0;
// Loop until escape
while ( ( count <= maxIters )
&& ((realPart*realPart + imagPart*imagPart) <= 4.0) ) {
++count;
// Update: z = z*z + z0;
double const oldRealPart = realPart;
realPart = realPart*realPart - imagPart*imagPart + realPart0;
imagPart = 2.0*oldRealPart*imagPart + imagPart0;
}
return count;
}
/** Main entry point.
* Works out where the current thread should read/write to global memory
* and calls doIterations to do the actual work.
*/
__global__ void processMandelbrotElement(
double * out,
const double * x,
const double * y,
const unsigned int maxIters,
const unsigned int numel ) {
// Work out which thread we are
size_t const globalThreadIdx = calculateGlobalIndex();
// If we're off the end, return now
if (globalThreadIdx >= numel) {
return;
}
// Get our X and Y coords
double const realPart0 = x[globalThreadIdx];
double const imagPart0 = y[globalThreadIdx];
// Run the itearations on this location
unsigned int const count = doIterations( realPart0, imagPart0, maxIters );
out[globalThreadIdx] = log( double( count + 1 ) );
}
//pctdemo_processMandelbrotElement.ptxw64
.version 4.2
// Copyright 2011 The MathWorks, Inc.
.target sm_20
.address_size 64
.visible .func (.param .b64 func_retval0) _Z20calculateGlobalIndexv(
)
{
.reg .s32 %r<11>;
.reg .s64 %rd<4>;
mov.u32 %r1, %ctaid.x;
mov.u32 %r2, %ctaid.y;
mov.u32 %r3, %nctaid.x;
mad.lo.s32 %r4, %r3, %r2, %r1;
mov.u32 %r5, %tid.x;
mov.u32 %r6, %ntid.x;
mov.u32 %r7, %tid.y;
mad.lo.s32 %r8, %r7, %r6, %r5;
cvt.u64.u32 %rd1, %r8;
mov.u32 %r9, %ntid.y;
mul.lo.s32 %r10, %r9, %r6;
mul.wide.u32 %rd2, %r10, %r4;
add.s64 %rd3, %rd2, %rd1;
st.param.b64 [func_retval0+0], %rd3;
ret;
}
.visible .func (.param .b32 func_retval0) _Z12doIterationsddj(
.param .b64 _Z12doIterationsddj_param_0,
.param .b64 _Z12doIterationsddj_param_1,
.param .b32 _Z12doIterationsddj_param_2
)
{
.reg .pred %p<3>;
.reg .s32 %r<7>;
.reg .f64 %fd<14>;
ld.param.f64 %fd7, [_Z12doIterationsddj_param_0];
ld.param.f64 %fd8, [_Z12doIterationsddj_param_1];
ld.param.u32 %r4, [_Z12doIterationsddj_param_2];
mov.u32 %r6, 0;
mov.f64 %fd12, %fd8;
mov.f64 %fd13, %fd7;
BB1_1:
mov.f64 %fd2, %fd13;
mov.f64 %fd1, %fd12;
mul.f64 %fd3, %fd1, %fd1;
mul.f64 %fd4, %fd2, %fd2;
add.f64 %fd9, %fd4, %fd3;
// 以下省略
function count = pctdemo_processMandelbrotElement(x0,y0,maxIterations)
%PCTDEMO_PROCESSMANDELBROTELEMENT Evaluate a Mandelbrot Set element
% m = pctdemo_processMandelbrotElement(x0,y0,maxIterations) evaluates the
% number of steps before the complex value (x0,y0) jumps outside a circle
% of radius two on the complex plane. Each iteration involves mapping
% z=z^2+z0 where z0=x0+i*y0. The return value is the log of the
% iteration count at escape or maxIterations if the point did not escape.
%
% See also: PARALLELDEMO_GPU_MANDELBROT
% Copyright 2011 The MathWorks, Inc.
z0 = complex(x0,y0);
z = z0;
count = 1;
while (count <= maxIterations) && (abs(z) <= 2)
count = count + 1;
z = z*z + z0;
end
count = log(count);使用GPU时容易遇到如下报错:The CUDA driver must recompile the GPU libraries because your device is more recent than the libraries.Recompiling can take several minutes. Learn more. 来自MATLAB官方网站的解答(https://ww2.mathworks.cn/matlabcentral/answers/437756-how-can-i-recompile-the-gpu-libraries): This is a known issue with CUDA 9.1 and the new Turing generation of GPUs. You don't need to do anything except ignore the initial warning or error. There are multiple issues. The warning about recompiling of libraries is spurious and not relevant. The error from cublas is one-time only. And there is an equivalent error in cuDNN. A permanent workaround is to put the following into your startup.m file:
warning off parallel:gpu:device:DeviceLibsNeedsRecompiling
try
gpuArray.eye(2)^2;
catch ME
end
try
nnet.internal.cnngpu.reluForward(1);
catch ME
end一共有两个startup.m文件,分别是 C:\Program Files\Polyspace\R2019a\toolbox\fixedpoint\fixedpointtool\+fxptui\Startup.m, C:\Program Files\Polyspace\R2019a\toolbox\matlab\external\interfaces\python\+python\+internal\startup.m, 我在这两个文件中都加了warning off parallel:gpu:device:DeviceLibsNeedsRecompiling ……,然而没用,警告还是会弹出。
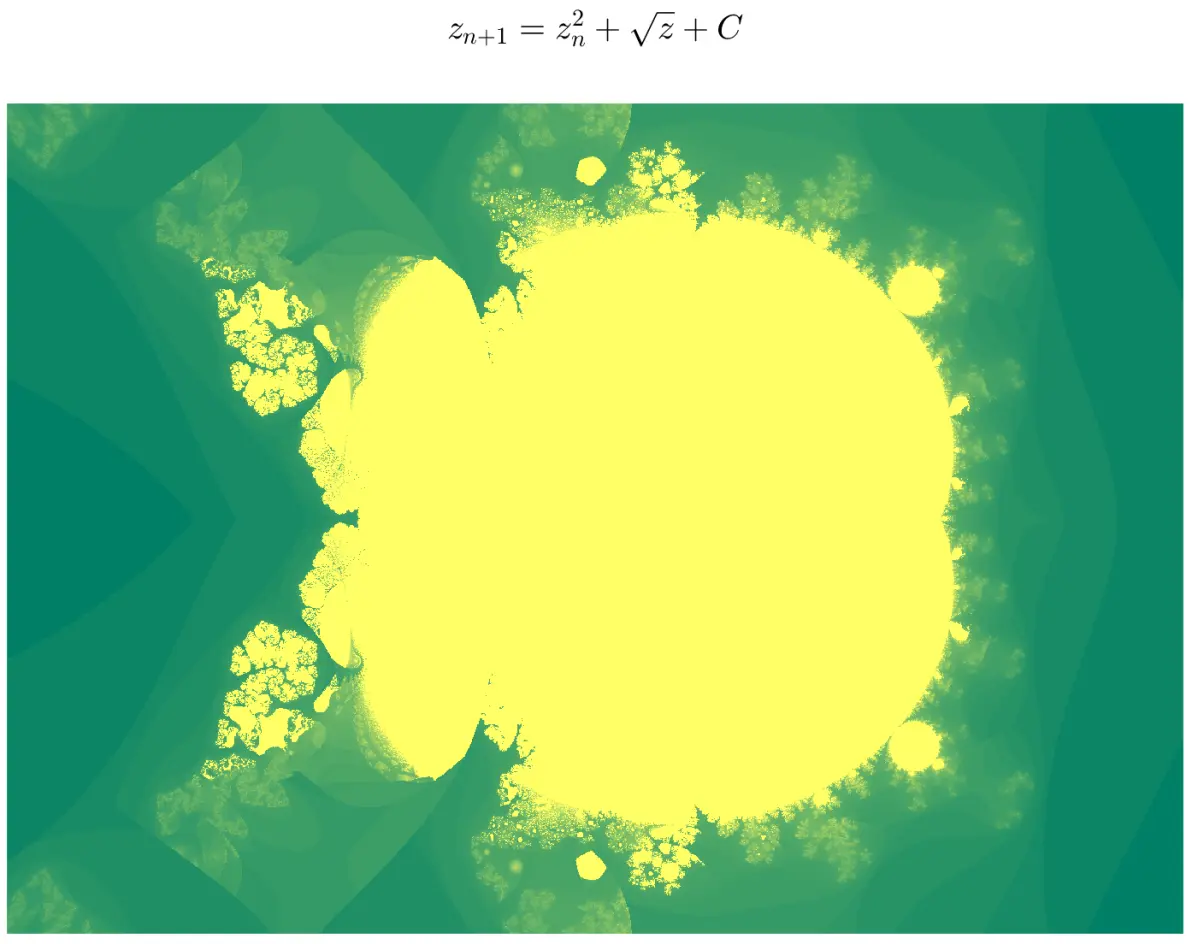
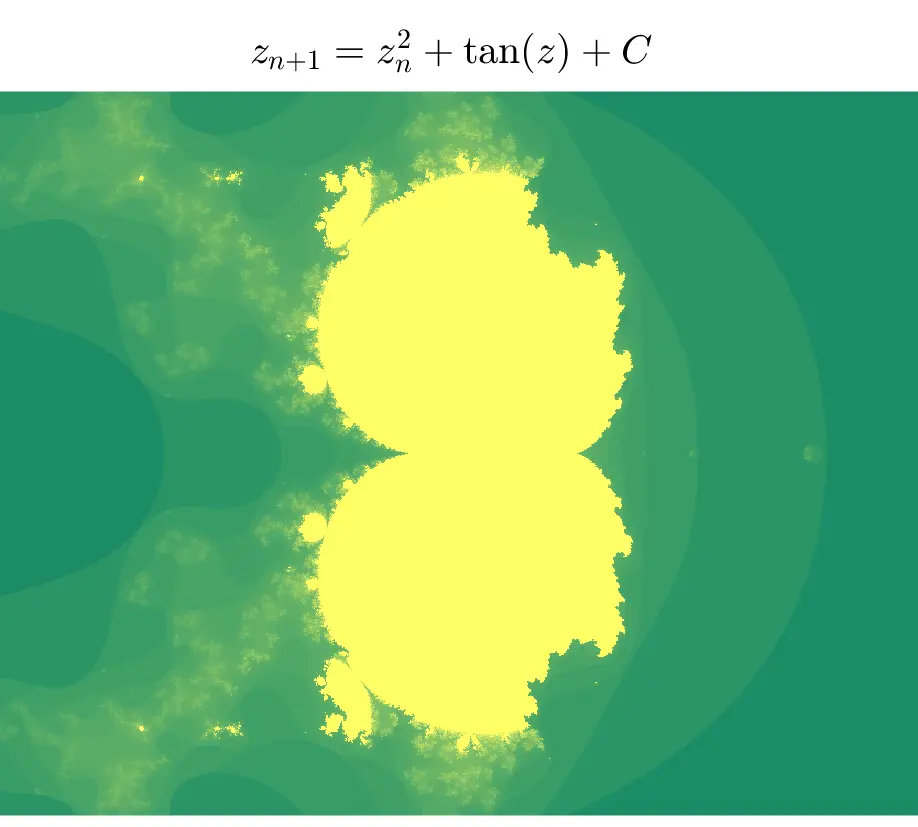
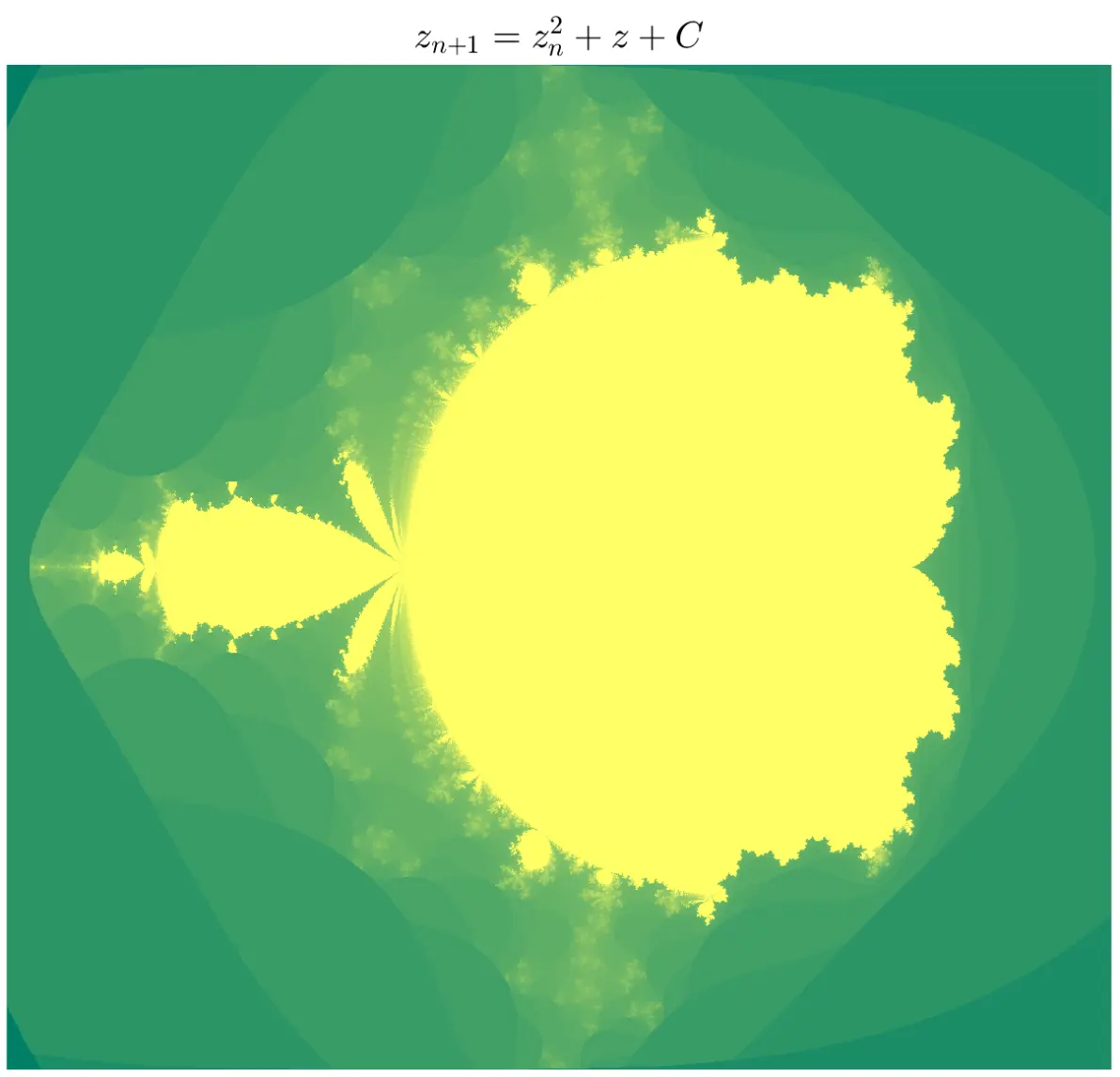
用其它形式的迭代公式生成的图形。