产品
输出(幅值矩阵,输出频率)=cwt输入(信号,采样频率)
[wt,f] = cwt(x,Fs);参考matlab官网例程:https://ww2.mathworks.cn/help/wavelet/ref/cwt.html?s_tid=doc_ta
其中两个复指数的连续小波变换(Continuous Wavelet Transform of Two Complex Exponentials)
frq1 = 32;
amp1 = 1;
frq2 = 64;
amp2 = 2;
Fs = 1e3;
t = 0:1/Fs:1;
x = amp1*sin(2*pi*frq1*t).*(t>=0.1 & t<0.3)+...
amp2*sin(2*pi*frq2*t).*(t>0.6 & t<0.9);
plot(t,x)
grid on
xlabel("Time (sec)")
ylabel("Amplitude")
title("Signal")
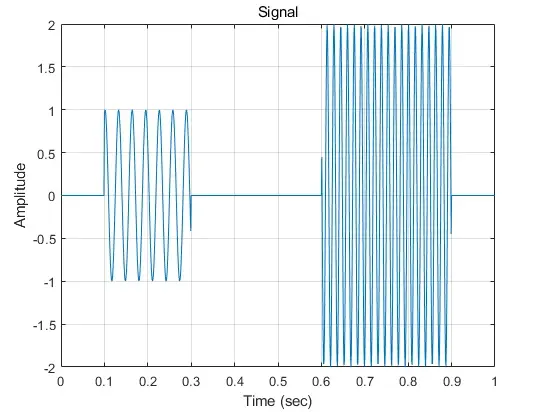
信号图
cwt(x,Fs)

小波分析结果
使用最初的函数应用形式——输出(幅值矩阵,输出频率)=cwt输入(信号,采样频率)
[wt,f] = cwt(x,Fs);查看输出数据wt和f,对应上图小波分析结果,查找f=66.81Hz的频率位于数组f中第28;

频率坐标
查找时间0.663s,应位于时间数组第664,对应查找输出矩阵wt(28,664)可得数据:0.786334025063183 + 1.725610240790233i
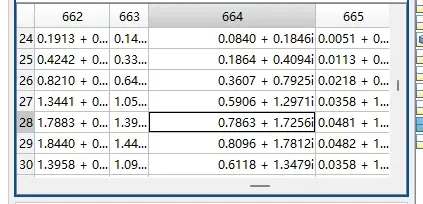
输出矩阵wt
计算abs(0.786334025063183 + 1.725610240790233i)=1.896325895539106,与小波分析结果标注幅值1.8963对应。
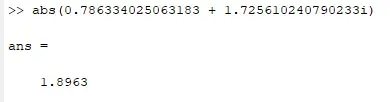
幅值计算
综上,输出(幅值矩阵,输出频率)=cwt输入(信号,采样频率)即[wt,f] = cwt(x,Fs),其中输出矩阵(x,y)的模值代表对应时间数组(y),频率数组(x)的幅值分析结果。